Українська   Deutsch
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2014 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Содержание

Введение

В настоящее время активно используются методы параллельного и распределенного программирования для решения различного рода задач. Таким образом, возникает необходимость в программном обеспечении, которое бы корректно и эффективно работало как на одном, так и на нескольких компьютерах, при условии, что некоторые задачи будут выполняться параллельно. Такой подход позволяет использовать программные и аппаратные ресурсы удаленных вычислительных систем, а также такая система является отказоустойчивой.

Вследствие повсеместного использования вычислительной техники происходит быстрое развитие в направлении численного моделирования. Численное моделирование является промежуточным элементом между аналитическими методами изучения и физическими экспериментами.

Использование численных моделей и кластерных систем позволяет значительно уменьшить стоимость процесса научного и технологического поиска. Кластерные системы в последние годы широко используются во всем мире как дешевая альтернатива суперкомпьютерам. Система требуемой производительности собирается из готовых, серийно выпускаемых компьютеров, объединенных, опять же, с помощью серийно выпускаемого коммуникационного оборудования. Это, с одной стороны, увеличивает доступность суперкомпьютерных технологий, а с другой, повышает актуальность их освоения, поскольку для всех типов многопроцессорных систем требуется использование специальных технологий программирования для того, чтобы программы могли в полной мере использовать ресурсы высокопроизводительной вычислительной системы [1].

Доминирующее положение при разработке параллельных программ для параллельных систем занимает стандарт MPI (англ. Message Passing Interface). Программа, разработанная в модели передачи сообщений, может быть представлена информационным графом, вершинам которого соответствуют параллельные ветви программы, а ребрам коммуникационные связи между ними. Это можно использовать для диспетчеризации заданий и их вычислительных потоков. Учитывая гетерогенность вычислительных ресурсов и сред передачи данных в кластере, можно осуществить распределение вычислительных потоков (ветвей) по вычислительным узлам так, чтобы минимизировать накладные расходы на обмен данными между потоками и выровнять вычислительную нагрузку между узлами. Для этого необходимо обладать информацией о мощности и загруженности узлов и структуре параллельных программ, которые ожидают выполнения [2].

1. Цель и задачи работы магистра

Целью данной работы является разработка параллельного MIMD-симулятора для СДО с распределенными параметрами.

Главными задачами являются:

2. Обзор существующих разработок по данной теме

Путем сотрудничества факультета КНТ со Штутгартским университетом развивается тема исследования разработки РПМС. Разработанные программы тестируются на кластерах Донецкого национального технческого университета и HLRS.

На глобальном уровне: Германия (М. Resch, M. Zeitz – The University of Stuttgart) [3,4], США, Великобритания, Китай.

На национальном уровне проблемами компьютерного моделирования занимаются киевские научные сотрудники: Томашевский В. Н., Жданова Е. Г. и Жолдаков А. А.

На локальном уровне проблемами разработки распределенных параллельных моделирующих сред занимались:

3. Распределенная параллельная моделирующая среда (РПМС)

РПМС является составной частью распределенных компьютерных систем (РКС). Каждый узел РКС представляет собой процессор с памятью. Выход одного узла из строя не приводит к отказу всей системы, поэтому такие системы являются отказоустойчивыми. Все компоненты параллельного программирования поддерживаются РПМС. Ее структура приведена на рисунке 1.

Рисунок 1 – Структурная организация параллельной моделирующей среды [6]

Рисунок 1 – Структурная организация параллельной моделирующей среды [6]

В РПМС должна быть обеспечена преемственность со средствами моделирования предыдущих поколений, которые сегодня реализованы в ЭВМ SISD-структуры. Тем самым параллельная распределенный моделирующая среда будет максимально дружественной к пользователю, позволит ему расти от моделей простых объектов к моделям сложных ДС, требующих параллельной реализации. Это будет означать открытость среды для пользователей и разработчиков моделей, работающих как индивидуально, так и коллективно, в зависимости от сложности проблемы моделирования. РПМС — это еще мало исследованный объект разработки и реализации. С целью систематизации разработок была предложена декомпозиция среды на следующие подсистемы [4]: диалога (ПД), параллельных решателей уравнений (ППРУ), обмена информацией (ПОИ), балансировка загрузки процессоров (ПБЗ), организации массивов данных (ПОМД), организации работы в режимах теледоступа пользователей (ПОРТД).

Реализация подсистем имеет принципиальное значение в определении поколения средств моделирования, к которому относится предлагаемая среду. Возможность моделировать в рамках одной среды системы с сосредоточенными и распределенными параметрами объединяет, с одной стороны, эти две области моделирования, которые развивались относительно автономно. С другой стороны, это универсализирует и затрудняет РПМС. Учитывая это обстоятельство приобретают важный методический вес проблемноориентированные моделирующие среды, построение которых может рассматриваться как составная часть общей проблемы и приобретения опыта параллельного моделирования сетевой динамической системы различной физической природы. Актуальной проблемой здесь является объектно-ориентированная разработка моделирующих сред, которая в наибольшей степени позволит использовать общие системно-программные решения в заданных предметных областях. Различные принципы действия и уровни распараллеливания SIMD- и MIMD-систем [7] обусловливают необходимость построения SIMD- и MIMD-компонент РПМС, решения задач их взаимодействия при реализации моделей параллельных динамических систем с сосредоточенными параметрами и моделей динамических систем с распределенными параметрами [8].

4. Минимальные требования к моделирующей среде

Процесс проектирования должен включать три составляющих: декомпозиция, связи, синхронизация.

Декомпозиция — это процесс разбиения задачи и ее решения на части [7]. Декомпозиция программных модулей определяет, какие функции они должны выполнять. Процесс моделирования составляет процесс перевода формул и алгоритмов в набор инструкций. Целью моделирования является копирование характеристик объекта и анализ его состояний при различных условиях. Декомпозиция определяет связи отдельных частей задачи. Для корректной работы моделируемого объекта части задачи должны быть связаны и синхронизированы.

Важной составляющей процесса разработки симулятора является выбор уровня распараллеливания.

5. Топологический анализ СДОРП

Структура сложных динамических систем характеризуется нелинейностью характеристик, большой размерностью и распределенностью параметров процессов, поэтому почти не поддается аналитическому анализу. Основным методом решения задач автоматизации и технологического проектирования является математическое моделирования. Формальное описание СДО состоит из двух важных частей: описания топологии и описания уравнений физических процессов, которые имеют место в ветвях и узлах сети [10]. Сетевые динамические объекты бывают двух типов: с распределенными параметрами (СДОРП) и концентрированными (СДОКП). СДОРП может представлять собой гидравлическую, электрическую или вентиляционную сеть. Топология динамического объекта представляется в виде графа G(u,v) с множеством узлов u=n и ветвей v=m. Аэродинамические процессы могут характеризироваться токами или давлениями и описываться системой уравнений. В качестве примера на рисунке 2 представлена топология сетевого динамического объекта вентиляционной сети.

Рисунок 2 – Топология СДОРП

где Bj — узлы, Qj — воздушные потоки, H(Q1) — вентилятор
Рисунок 2 – Топология СДОРП

Дискретной Simulation-моделью (DSM) ветви любого объекта является система уравнений, которая получается в результате применения некоторого численного метода для решения системы уравнений. Симулятор — это программно-аппаратная реализация DSM. Для j-ветви сети (рис. 3) можно составить DSM (формула 1).

Рисунок 3 — Граф СДОРП в линейном виде

Рисунок 3 — Граф СДОРП в линейном виде

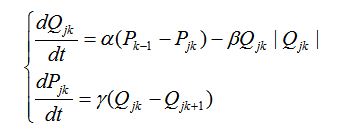Формула,    (1)
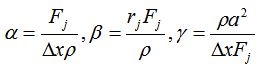
где Формула

MIMD-процесс минимальной гранулярности для динамических систем представляет собой процесс, ответственный за решение задачи Коши относительно одной искомой переменной.

Формула     (2)

Распараллеливание вычислений правой части вектора Х задачи Коши нецелесообразно в связи с увеличением объема операций обмена. Виртуальная параллельная DSM — это совокупность MIMD-процессов минимальной гранулярности. Проблемой является отображение 1:1 процессов минимальной гранулярности на целевой параллельной вычислительной системе.

6. Уровни распараллеливания

Параллельную модель можно представить на четырех уровнях, которые изображены на рисунке 4.

Рисунок 4 – Уровни распараллеливания

Рисунок 4 — Уровни распараллеливания
(анимация: 7 кадров, 3 циклов повторения, 16 килобайт)

Первый уровень: 1 уравнение — 1 процесс. Уровень минимальной гранулярности.

Второй уровень: 1 элемент — 1 процесс.

Третий уровень: 1 ветвь — 1 процесс.

На рисунке 5 представлена схема DSM на третьем уровне распараллеливания.

Четвертый уровень: 1 подграф — 1 процесс. Граф декомпозируется на подграфы, имеющие наименьшее количество связей друг с другом. В этом случае количество процессов зависит от числа подграфов, на которые разбивают СДОРП [11].

Рисунок 5 - DSM на третьем уровне распараллеливания (анимация: 7 кадров, 3 циклов повторения, 16 килобайт)

Рисунок 5 — DSM на третьем уровне распараллеливания

Существует 2 варианта реализации третьего уровня распараллеливания [3]. Их сравнение приведено в таблице 1 по следующим критериям:

  1. Равномерность загрузки
  2. Соотношение Nоо/Nобм
  3. Виртуальное ускорение с учетом операций обмена
  4. Схема связи между процессами
  5. Количество Q- и P-процессов

Таблица 1 — Варианты реализации третьего уровня распараллеливания

Критерий Вариант 1 Вариант 2
Равномерность загрузки
L — количество уравнений, решаемых в процессе;М — количество веток СДО;шаг по пространственной координате 		Загрузка (QP)j процессов Lj=2Mj=lj/Δξ зависит от количества решаемых уравнений и разброса длин lj веток. Неравномерность ΔL=Lmax-Lmin=2(Mjmax-Mjmin), учитывая диапазон длин [100..2000], будет существенной. Каждый из Npj+1 процессов решает не менее, чем Mmin=ljmin/Δξ пар уравнений. Достигнута формализация планирования и равномерного распределения загрузок процессов по предложенному алгоритму.
Соотношение Nоо/Nобм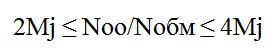
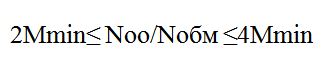
Виртуальное ускорение с учетом операций обмена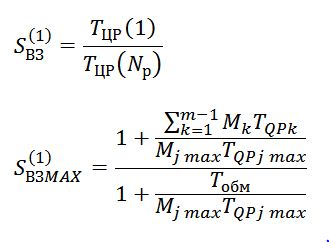
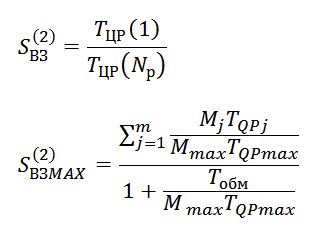
Схема связи между процессами Предложены виртуальные PQ- и QP-коммутаторы, работа которых организуется таким образом: схема связей между процессами реализуется к началу работы и остается неизменной на весь период моделирования; в i-м цикле вычислений запоминаются компоненты векторов Qj(ih) Pj(ih) и записываются в исходные регистры Q- и P-процессов; все процессы синхронизируются по моменту завершения самого длинного процесса, синхронно для всех Q- и P-процессов активируются команды обмена, в один такт на входах Q- и P-процесов появляются актуальные значения переменных и следующим тактом записываются в память; запускается i+1-й цикл вычислений. На всех уровнях коммутаторы реализуются однотипно на базе переключателей 2х2.
Количество Q- и P-процессов

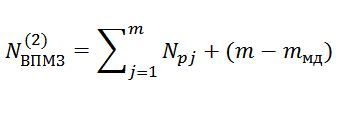
Список источников

  1. Букатов А. А., Дацюк В. Н., Жегуло А. И. Программирование многопроцессорных вычислительных систем. — Ростов-на-Дону: ООО «ЦВВР», 2003. — 208 с.
  2. Высокопроизводительные параллельные вычисления на кластерных системах — Материалы Седьмой Международной конференции-семинара, Нижний Новгород, 26–30 ноября 2007 г.
  3. Forschungsgebiet: parallele Simulationstechnik [Электронный ресурс] / L. P. Feldmann, V.A. Svjatnyj, M. Resch, M. Zeitz — Режим доступа: http://www.nbuv.gov.ua/, свободный.
  4. Svjatnyj V.A., Nadeev D.V., Solonin O.M., Rothermel K., Zeitz M.: Subsysteme einer verteilten parallelen Simulationsumgebung fur dynamische Systeme. 16. Symposium ASIM 2002, Tagungsband, 2002.
  5. Святний B.A., Молдованова O.B., Перерва А.О. Проблемно-орієнтоване паралельне моделююче середовище для динамічних мережних об'єктів. Наукові праці ДонНТУ, серiя «Проблеми моделювання та автоматизації проектування» (МАП-2001). Випуск: 29 – Донецьк: ДонНТУ. – 2001.
  6. Святний В.А. Проблеми паралельного моделювання складних динамічних систем. Наукові праці ДонДТУ, Серія «ІКОТ», вип. 6, 1999.
  7. Хьюз Т., Хьюз К. Параллельное и распределенное программирование на С++. : Пер. с англ. – М. : Издательский дом «Вильямс», 2004 – 672с.
  8. Скворцов П.В. Разработка и исследование решателя уравнений параллельной моделирующей среды на основе OpenMP-стандарта [Электронный ресурс]. — Режим доступа:http://masters.donntu.ru, свободный.
  9. Anoprienko A.J., Svjatnyj V.A., Braunl T., Reuter A., Zeitz M.: Massiv parallele Simulationsumgebung fur dynamische Systeme mit konzentrierten und verteilten Parametern. 9. Symposium ASIM’94, Tagungsband, Vieweg, 1994, S. 183-188.
  10. Гусєва Г.Б., Молдованова О.В. MIMD-паралельний вирішувач рівнянь для мережного динамічного об’єкту з розподіленими параметрами. Проблемы моделирования и автоматизации проектирования динамических систем: Сборник научных трудов ДонНТУ, вып. 6, 2007.
  11. Скорич В.И. Априорный анализ виртуальных параллельных моделей управляемого сетевого динамического объекта с распределенными параметрами [Электронный ресурс]. — Режим доступа:http://masters.donntu.ru, свободный.