Назад в библиотеку
Применение генетических алгоритмов для обучения исскуственных нейронных сетей при решении задач прогнозирования временных рядов
Автор: А.А. Яковенко
Источник: Яковенко А.А. Применение генетических алгоритмов для обучения исскуственных нейронных сетей при решении задач прогнозирования временных рядов
/ Яковенко А.А. // Сборник научных трудов НГТУ – № 4(46) 2006, C.61–66.
ВВЕДЕНИЕ
Традиционные алгоритмы обучения искусственных нейронных сетей
(ИНС) довольно успешно применяются для задач прогнозирования времен-
ных рядов [1]. Однако при решении некоторых задач из этого класса данные
методы дают слишком большую погрешность прогнозирования, в частности
при попытке получения прогноза притока воды в реках [2, 3].
Для решения указанной проблемы предлагаем использование ИНС, обу-
чаемых при помощи генетических алгоритмов. Генетические алгоритмы обуче-
ния подразумевают искусственную эволюцию ИНС с целью поиска наилучшей
(наиболее приспособленной для решения поставленной задачи) нейронной сети.
В данной работе на примере задачи прогнозирования среднедекадного притока
воды в створе Новосибирской ГЭС (под декадой в данном случае понимается
период, равный 10 дням) исследована эволюция нейронных сетей как с изме-
няющейся, так и постоянной топологией (с изменяющимися весовыми коэффи-
циентами соединений между нейронами).
ПОСТАНОВКА ЗАДАЧИ
В процессе эксплуатации Новосибирской ГЭС неизбежно возникают
трудности, связанные с оптимальным управлением работой водохранилища.
Одна из основных проблем – отсутствие точного прогноза притока.
Цель настоящего исследования – возможность прогнозирования декадного притока
на основе исходных данных только о предыстории изменения притока во времени.
В ходе работы применялся метод вариативного моделирования, предполагающий построение и совместное использование набора моделей. В рамках
этого метода для прогнозирования притока изучалась пригодность нейросетей, обучаемых при помощи генетических алгоритмов.
ИСХОДНЫЕ ДАННЫЕ И УСЛОВИЯ ИССЛЕДОВАНИЯ
Исходные данные исследования представляют собой гидрологические
временные ряды среднедекадного расхода притока (м3/с) реки Обь в створе
Новосибирской ГЭС за 1977–2005 гг.
Прогноз очередного среднедекадного значения притока осуществлялся
путем подачи нормализованных значений притока за некоторое количество
предыдущих декад на входы ИНС (см. выражение (1)) и получения нормализованного же значения прогноза притока для интересующей декады на выходе
нейросети (см. выражение (2)).
Значения притока, подаваемые на входы нейросети, вычислялись следующим образом:
xi = Li 0,0001, (1)
где xi – значение сигнала, подаваемого на i-й вход нейросети; Li – значение
притока (м3/с) по каждой из трех предыдущих декад. Таким образом, гипоте-
тический максимум притока (10 000 м3/с) должен отвечать значению 1,0 на
соответствующем входе нейросети.
С выходов нейросети снималось предсказанное значение притока в соот-
ветствии со следующим выражением:
L = y10000, (2)
где y – значение сигнала, получаемого на выходе нейросети; L – прогнозируе-
мое значение притока (м3/с) для выбранной декады конкретного месяца.
Текущая ошибка предсказания n-й нейросети в каждом поколении вычис-
лялась в соответствии со следующей формулой:
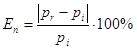 (3)
(3)
где pr – предсказанное значение притока для конкретной декады конкретного
месяца, pi – реальное значение притока.
Исследование велось в двух направлениях. Первое подразумевало, что в
процессе обучения структура ИНС не изменяется (менялось лишь значение
коэффициентов весов связей между нейронами), а второе – что в процессе
обучения помимо значений весовых коэффициентов может изменяться количество нейронов в промежуточном (скрытом) слое.
В каждом случае для получения новых поколений ИНС использовали два
генетических оператора – мутации и селекции. Хромосома, соответствующая
каждой нейросети, представляла собой набор вещественных чисел, каждое из
которых было равно по значению соответствующему весовому коэффициенту
нейросети.
В процессе эволюции ИНС постоянно отбирались те из них, которые обладали минимальной средней ошибкой предсказания для выбранной декады
на протяжении всей обучающей выборки. Эволюция считалась законченной,
если средняя ошибка предсказания последней из найденных «лучших» ИНС
становилась меньшей либо равной 1 % или если количество итераций превышало некоторое пороговое значение.
В обучающую выборку входили данные среднедекадного притока для интересующей декады за предыдущие годы. Размер обучающей выборки посто-
янно увеличивался: изначально он был равен 12 годам (при этом подсчитывалась ошибка прогноза на 13-й год в соответствии с выражением (3)), затем 13
годам (подсчитывалась ошибка прогноза на 14-й год) и т. д. После достижения максимально возможного размера обучающей выборки (определяется
полным объемом имеющихся в наличии данных) вычислялась усредненная
ошибка прогнозирования.
В случае с ИНС, имеющими постоянную структуру, использовали модель
полносвязного персептрона с одним скрытым слоем (рассматривали персептроны с 5, 10, 20 и 50 нейронами в скрытом слое), четырьмя входами и одним
выходом. При помощи специализированного ПО было выявлено, что значения притока именно для последних четырех предшествующих декад наиболее
сильно влияют на значение притока для большинства декад (инструмент Find
Dependences системы ИАД PolyAnalyst). Поэтому на входы такого персептрона в каждом случае подавали значения притока именно за предыдущие четыре
декады.
В случае с ИНС, имеющими переменную структуру, также использовали
персептрон с одним скрытым слоем, но количество нейронов в этом слое по-
стоянно увеличивалось в процессе обучения (от 1 до 25 нейронов). При этом
очередной нейрон добавляли в сеть после каждых 50 000 итераций эволюци-
онного процесса. Веса добавляемых нейронов генерировались случайным
образом (небольшие вещественные числа от 0 до 0.1). Кроме того, количество
входов ИНС для получения прогноза подбирали индивидуально для каждой декады на основе результатов предварительного этапа эволюции (определяли
количество входов ИНС, способствующее появлению в процессе эволюции
нейросети, обладающей минимальной ошибкой прогнозирования).
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
Результаты проведенных экспериментов (усредненные значения ошибки
прогнозирования притока для различных декад каждого месяца, полученные
при помощи двух описанных выше методов) приведены в таблице. Для сравнения в таблице также даны усредненные значения ошибки прогноза притока,
полученные от Западно-Сибирского Гидрометцентра.
Результаты прогнозирования среднедекадного притока
| Период | Средняя ошибка, % |
| За 1977–2005 гг.(ИНС с постоянной структурой) | За 1977–2005 гг.(ИНС с изменяемой структурой) | За 1993–2005 гг.(прогноз Гидрометцентра) |
| Январь1 | 5,5 | 7.9 | 6,2 |
| Январь2 | 3,6 | 11.0 | 4,4 |
| Январь3 | 5,1 | 9.2 | 6,7 |
| Февраль1 | 4,2 | 8.5 | 3,2 |
| Февраль2 | 3,2 | 5.3 | 2,7 |
| Февраль3 | 3,5 | 7.9 | 2,6 |
| Март1 | 2,9 | 3.8 | 1,7 |
| Март2 | 3,6 | 4.2 | 1,5 |
| Март3 | 11,3 | 8.9 | 8,0 |
| Апрель1 | 32,8 | 31.3 | 14,0 |
| Апрель2 | 55,7 | 48.0 | 18,5 |
| Апрель3 | 33,5 | 22.5 | 10,1 |
| Май1 | 22,5 | 20.9 | 6,5 |
| Май2 | 19,2 | 16.1 | 4,9 |
| Май3 | 13,5 | 22.7 | 6,6 |
| Июнь1 | 17,7 | 18.2 | 5,3 |
| Июнь2 | 21,0 | 13.6 | 6,0 |
| Июнь3 | 25,3 | 21.7 | 4,2 |
| Июль1 | 17,1 | 17.0 | 5,4 |
| Июль2 | 13,4 | 17.0 | 7,0 |
| Июль3 | 12,6 | 9.4 | 6,6 |
| Август1 | 17,0 | 16.8 | 4,2 |
| Август2 | 18,8 | 21.2 | 9,0 |
| Август3 | 13,2 | 18.2 | 9,0 |
| Сентябрь1 | 11,7 | 16.2 | 4,3 |
| Сентябрь2 | 16,0 | 20.6 | 4,4 |
| Сентябрь3 | 12,8 | 18.3 | 5,5 |
| Октябрь1 | 17,0 | 18.7 | 6,5 |
| Октябрь2 | 13,6 | 14.3 | 6,7 |
| Октябрь3 | 9,1 | 15.4 | 15,9 |
| Ноябрь1 | 13,6 | 20.3 | 7,9 |
| Ноябрь2 | 16,5 | 19.7 | 13,1 |
| Ноябрь3 | 15,0 | 19.6 | 9,0 |
| Декабрь1 | 8,7 | 15.5 | 7,3 |
| Декабрь2 | 7,7 | 7.9 | 5,4 |
| Декабрь3 | 5,8 | 11.9 | 4,1 |
Результаты проведенного исследования показали, что использование ИНС
с неизменяемой структурой позволяет получить меньшую ошибку прогнозирования для лета, зимы и поздней осени, а ИНС с переменным количеством
нейронов в скрытом слое – для апреля – мая, июня и августа. Скорее всего, это
вызвано традиционно более хаотичным и нелинейным изменением притока в
весенние и осенние месяцы, что требует более сложной структуры используемой ИНС. Что же касается остальных, более спокойных и предсказуемых сезонов, то достаточно гораздо меньшего количества нейронов в скрытом слое,
для которого оптимальный набор весов связей ИНС можно определить за
меньшее количество итераций эволюционного процесса.
ЗАКЛЮЧЕНИЕ
По результатам проведенного исследования можно сделать вывод: используемая модель нейронной сети, обучаемая при помощи генетических алгоритмов указанными выше способами, обеспечивает приемлемо достоверный прогноз притока воды р. Обь для периода с конца октября по конец марта. Ошибка прогнозирования для этих периодов сопоставима с ошибкой прогноза Гидрометцентра, а для отдельных декад она даже меньше (январь и конец октября). Наихудший прогноз (наибольшее значение ошибки) получен
при попытке предвидеть подъем воды на апрель – июнь, что вполне закономерно, поскольку во время весеннего паводка на уровень притока влияет
большое количество внешних факторов, многие из которых технически сложно отследить [4].
Для улучшения качества прогнозирования (уменьшения значения средней
ошибки получаемых прогнозов) в дальнейшем предполагается:
- разработать эффективные методики увеличения количества слоев ИНС в процессе обучения при помощи генетических алгоритмов и исследовать ее применимость для решения задачи прогнозирования;
- исследовать различные методы деления нейронов в процессе обучения
при помощи генетических алгоритмов, поскольку простое добавление нейрона со случайно сгенерированными весами снижает статистическую обоснованность результатов прогнозирования.
СПИСОК ИСТОЧНИКОВ
- Осовский С. Нейронные сети для обработки информации / Пер. с польск.И.Д. Рудинского. – М.: Финансы и статистика, 2002.
- Гаврилов А.В., Канглер В.М. Использование искусственных нейронных сетей для анализа данных // Сб. науч. трудов НГТУ. – 1999. – № 3(16). – С. 56–63.
- Гаврилов А.В. Гибридные интеллектуальные системы. – Новосибирск:Изд-во НГТУ, 2003.
- Владимиров А.М. Гидрологические расчеты. – Л.: Гидрометеоиздат,1990.
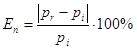 (3)
(3)