Floating-Point Arithmeti

Автор перевода - Русинка Б. В.

Floating-Point Arithmetic

1.3 Некоторое странное поведение

Проектирование эффективных и надежных аппаратных или программных систем с плавающей запятой является сложной и несколько рискованной задачей. Некоторые известные ошибки были широко обсуждены ранее; напомним некоторые из них ниже. Кроме того, даже когда арифметика

без недостатков, может иногда возникать некоторое странное поведение, только потому, что они соответствуют численным проблемам, которые действительно сложные. Все это не удивительно: отображение непрерывных действительных чисел на конечной структуре (числа с плавающей точкой) не может быть сделано без каких-либо проблем.

1.3.1 Некоторые известные ошибки

• Делитель первой версии процессора Intel Pentium, выпущенный

в 1994 году, имел недостаток. В исключительно редких случаях, можно было бы получить три верных знака. Например, вычисление

8391667/12582905

даст 0.666869… вместо 0.666910….

• С версии 7.0 системы компьютерной алгебры Maple, при вычислении

1001!/1000!,

мы получим 1 вместо 1001.

• С предыдущей версии (6.0) той же системы, при входе числа

+21474836480413647819643794

вы получите

413647819643790) + -. (-. (

• Каган упоминает некоторые странное поведение в некоторых версиях Эксел таблицах. Они, кажется, были связаны с попыткой имитировать десятичную

арифметику на основе двоичной системы.

Еще более яркий поведение происходит с некоторыми ранними версиями Excel 2007:
При попытке вычислить

65536 - 2^-37

отображается результат 100001. Это ошибка преобразования из двоичной к

десятичной системе используется для отображения этого результата: внутреннее значение правильно, если вы добавите 1 к этому результату Вы получаете 65 537. Объяснение можно найти на

http://blogs.msdn.com/excel/archive/2007/09/25/calculation-issue-update.aspx, а патч можно получить тут http://blogs.msdn.com/excel/archive/2007/10/09/расчетно-эмиссионных обновление-исправление-available.aspx

• Некоторые баги не требуют программную ошибку: они обусловлены слабой спецификацией. Например, зонд Mars Climate Orbiter разбился на

Марсе в сентябре 1999 года из-за удивительной ошибки: одна из

команд, которые предназначены численное программное обеспечение принимала за единицу расстояния метр, в то время как другая команда предположила, что это были футы.

Очень аналогично, в июне 1985 года, космический челнок расположил себя, чтобы получить лазерный сигнал от вершины горы, которая предположительно была 10 000 миль в высоту, вместо правильного 10000 футов.

1.3.2 Сложные проблемы

Иногда, даже с правильно реализованной арифметикой с плавающей точкой,

результат вычислений далек от того, который можно было бы ожидать.

Последовательность, кажется, сходится к неправильному пределу

Рассмотрим следующий пример, спасибо одному из нас и проанализированному Каганом. Пусть (U_n) будет последовательностью, определенной как:

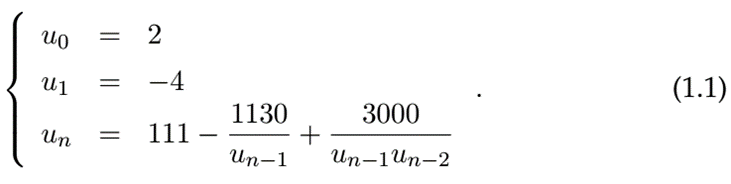
Легко показать, что предел этой последовательности 6. И все же, на любой системе с любой точностью, последовательность будет, кажется, стремиться к 100.

Например, в таблице 1.1 представлены результаты, полученные при составлении программ 1.1 и запущенных его на Pentium 4 на базе, с использованием GNU, коллекции компиляторов (GCC) и системе Linux.

Объяснение этого странного явления довольно проста. Общее

Решение для последовательности

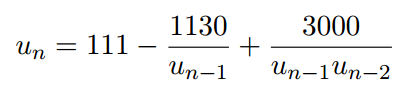это

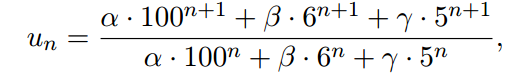
где α, β, γ и зависит от начальных значений и начальных значений U₀ и U₁. Поэтому, если α ≠ 0, то предел последовательности 100, в противном случае (при условии, β ≠ 0), то равен 6. В данном примере, начальные значения U₀=2 и U₁= -4 были выбраны так что α = 0, β = -3, и γ = 4. Таким образом, "точный" предел функции равен 6. И все же, при вычислении значения U_n

в арифметике с плавающей точкой, используя систему 1.1, из-за различных ошибок округления, даже самые первые вычисленные условия

немного отличаются от точных значений. Следовательно, значение α, соответствующее этим вычисленным терминам очень мало, но отлично от нуля. Этого достаточно, чтобы сделать

вычисляемую последовательность "сходящейся" до 100.

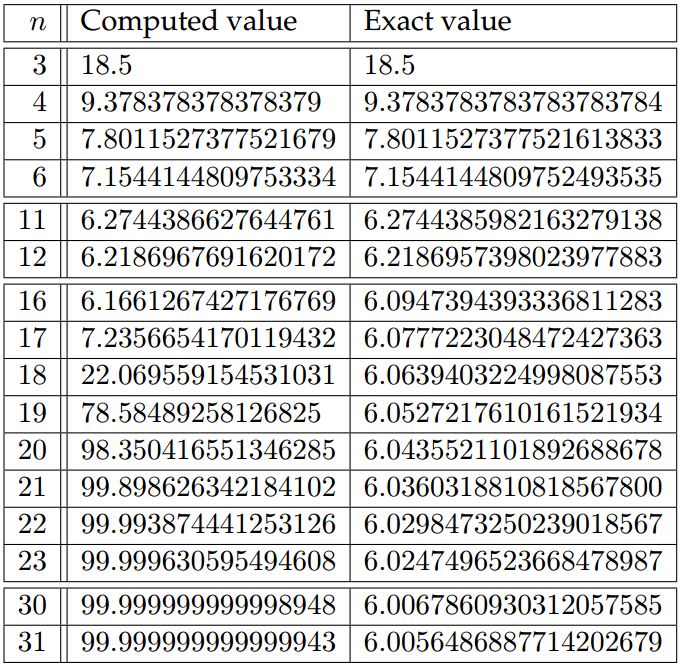
Таблица 1.1 - Результаты, полученные в программе 1.1 на Pentium 4, используя GCC и систему Linux, по сравнению с точными значениями последовательности

Банковское Общество The Chaotic

Недавно г-н Доверчивый пошел в банка общества The Chaotic, чтобы узнать больше о новом виде счета, который они предлагают своим лучшим клиентам. Ему сказали:

Ваш первый депозит $е - 1 на вашем счету, где е = 2,7182818…

это основание натуральных логарифмов. Первый год, мы берем $1

с Вашего счета в качестве банковских сборов. Второй год еще лучше

для вас: мы умножаем ваш капитал на 2, и мы берем $1 банковских сборов. Третий год еще лучше: мы умножаем ваш капитал на 3, и мы берем $1 банковских сборов. И так далее: до n-го года, ваш капитал умножается на n, и мы просто берем $1 за услуги. Интересно, не так ли?

Г-н Доверчивый хотел, чтобы его сбережения были в безопасности. Поэтому, прежде чем принимать предложение, он решил выполнить некоторое моделирование на его собственном компьютере, чтобы видеть то, что

его капитал будет представлять через 25 лет. Вернувшись домой, он написал программу на C. (Программа 1.2).

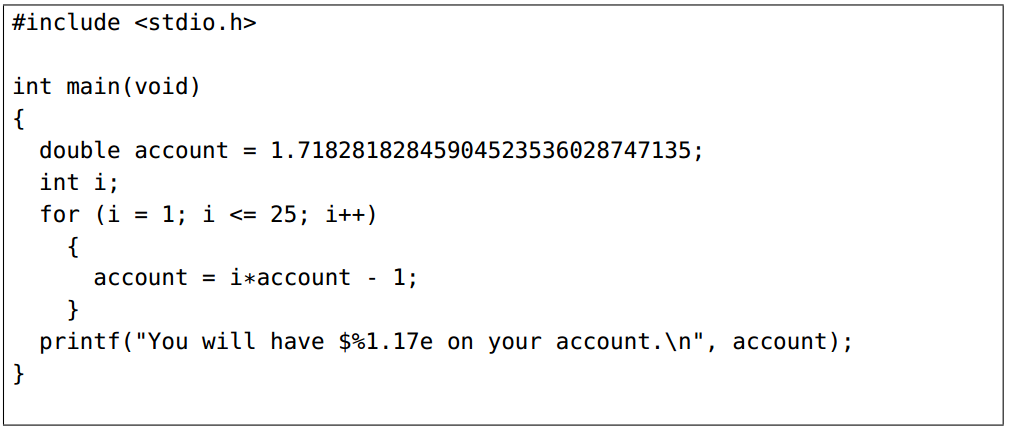
Программа 1.2: программа г-на Доверчивого на C.

На своем компьютере (с процессором Intel Xeon и GCC на Linux, но

странные вещи происходят с любым другим оборудованием), он получил следующий результат:

Вы будете иметь $ 1.20180724741044855e +09 на вашем счету.

Таким образом, он сразу же решил принять предложение. Он, безусловно, будет грустно разочарован, 25 лет спустя, когда он поймет, что он на самом деле имеет около $ 0,0399 на своем счету.

Что происходит в этом примере легко понять. Если вы назовете

а₀ размером первоначального депозита и а_n депозит после окончания n года, тогда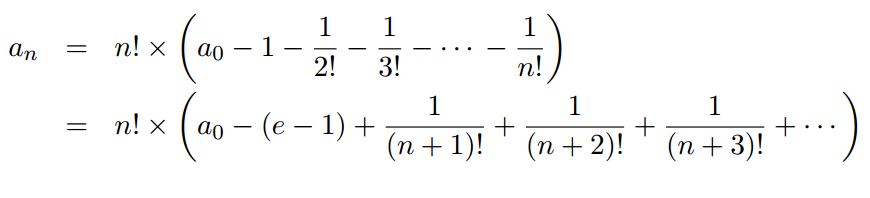

так что:

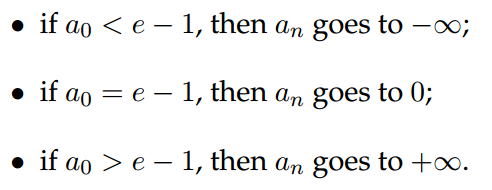
В нашем примере а₀=е-1, поэтому точная последовательность а_n стремится к нулю. Это объясняет, почему точное значение а₂₅ настолько мало. И все же, даже если арифметика операции была безошибочная (что, конечно же не так), так как е - 1 не точно представима в арифметике с плавающей точкой, вычисленная последовательность будет стремиться к + ∞ или - ∞, в зависимости от направления округления.

Пример Румпа

Рассмотрим следующую функцию, разработанную Зигфридом Румпом в 1988 году,

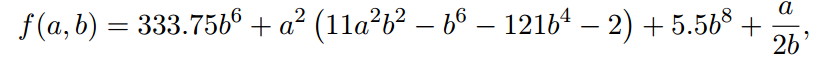
и попытаться вычислить f (а, b) при а = 77617,0 и b = 33096,0. На IBM 370, результаты, полученные Румпом были

• 1.172603 с одинарной точностью;

• +1,1726039400531 с двойной точностью и

• +1,172603940053178 с повышенной точностью.

Любой глядя на эти цифры скажет, что результат даже одинарной точности, конечно, очень точный. И все же, точный результат -0,8273960599….

На более поздних системах, мы не видим того же самого поведения. Например, используя Pentium 4, с использованием GCC и систему Linux,

программа C (Программа 1.3), которая использует двойную точность вычислений, вернет 5.960604 × 10²⁰, в то время как его эквивалент одинарной точности вернет 2,0317 × 10²⁹, а эквивалент повышенной точности вернет -9,38724 × 10^-323. Мы по-прежнему получаем совершенно неверные результаты, но по крайней мере, ясно - различия между ними показывают, что что-то странное происходит.

Программа 1.3 – Пример Румпа