Прогнозирование количества травм с использованием метода Бокса-Дженкинса

Авторы: Д.М. Сапицкая, С.В. Хмелевой

Постановка проблемы.

Прогнозирование количества травм – задача, которой на данный момент занимаются в основном с целью повышения качества охраны труда на предприятии. Основной задачей прогнозирования травматизма является выявление закономерностей изменения и конкретной величины статистических его показателей в будущем, а также определение неблагоприятных тенденций основных показателей, особенно травмирующих факторов, требующих принятия плановых решений.

Входными данными для анализа служат показатели количества обращений в Областную травматологию г. Донецка с 2004 по 2012 гг. Данные разделены по месяцам и представляют собой временной ряд.

Описание метода прогнозирования.

Подход Бокса-Дженкинса является одним из лучших методов, позволяющих нам понять и прогнозировать временные ряды.

Общий вид процедуры использования метода Бокса-Дженкинса можно представить следующим образом:

В семействе ARIMA-процессов Бокса-Дженкинса выбирается достаточно простой процесс, позволяющий получить данные, которые в целом выглядят примерно так же, как наш ряд (за исключением фактора случайности). Для этого необходимо выбрать конкретный тип модели и оценить требуемые параметры на основе своих данных. Из результирующей модели можно узнать в какой мере каждое наблюдение влияет на будущее и в какой мере каждое наблюдение содержит полезную новую информацию, позволяющую прогнозировать будущее.
Прогноз на любой момент времени представляет собой ожидаемое (т.е. среднее) будущее значение оцениваемого процесса в этот момент времени. Формула для прогноза позволяет быстро вычислить среднее значение для бесчисленного множества вариантов поведения ряда, начиная с исходных данных и экстраполируя их в соответствии с выбранной моделью.
Стандартная ошибка прогноза для любого момента времени представляет собой стандартное отклонение от всех возможных (допустимых) будущих значений для этого времени.[1]
Границы прогноза простираются выше и ниже прогнозируемого значения так, что (если выбранная модель оказалась правильной) с вероятностью, например, 95% можно утверждать. что будущее значение для любого момента времени уложится в указанные границы прогноза. Эти границы прогноза формируются таким образом, чтобы для каждого будущего периода времени 95%, возможных (и допустимых) вариантов будущего поведения ряда укладывались в эти границы. [2]

ARIMA-процессы Бокса-Дженкинса представляют собой семейство линейных статистических моделей. основанных на нормальном распределении, которые позволяют имитировать поведение множества различных временных рядов путем комбинирования процессов авторегрессии, процессов интегрирования и процессов скользящего среднего.

Процесс случайного шума состоит из случайной выборки (независимых наблюдений) из нормального распределения с постоянным средним и стандартным отклонением. Какие-либо тенденции (тренды) в этом случае отсутствуют, поскольку – по причине независимости – наблюдения не помнят о прошлом поведении ряда.

В соответствии с моделью случайного шума в момент времени t наблюдаемые данные будут состоять из константы, µ (долгосрочное среднее значение процесса), плюс случайный шум с нулевым средним значением.

Модель процесса случайного шума:

Долгосрочное среднее значение Y равно µ.

Любое наблюдение процесса авторегрессии представляет собой линейную функцию от предыдущего наблюдения плюс случайный шум. Таким образом, процесс авторегрессии помнит о своем предыдущем состоянии и использует эту информацию для определения своего дальнейшего поведения.

Модель процесса авторегрессии:

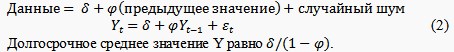
Процесс случайного среднего не помнит в точности своего прошлого, но помнит компонент случайного шума того состояния, в котором он (процесс) находился. Таким образом, его память ограничена одним шагом в будущее; за пределами этого шага для процесса все начинается заново.

Модель процесса случайного среднего:

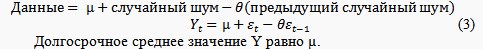
Процесс авторегрессии и скользящего среднего запоминает как свое предыдущее состояние, так и компонент случайного шума предыдущего состояния. Таким образом, его память сочетает в себе память процесса авторегрессии с памятью процесса скользящего среднего. В результате получается процесс авторегрессии с улучшенной краткосрочной памятью.[3]

Если изменения или разности в ряде вырабатываются процессом авторегрессии скользящего среднего, то сам этот ряд соответствует процессу авторегрессионного интегрированного скользящего среднего (ARIMA)(autoregressive integrated moving-average process). Этот процесс знает, где он находится, помнит, как он попал в это состояние и помнит даже часть предыдущего шумового компонента. Следовательно, ARIMA-процесс можно использовать в качестве модели для совокупностей данных временного ряда, которые являются очень гладкими, с медленными изменениями направления. Эти ARIMA-процессы являются нестационарными из-за включения в них интегрированного компонента.

Модель процесса авторегрессионного интегрированного скользящего среднего (ARIMA) в разностной форме:

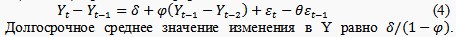
Нельзя рассчитывать, что с течением времени Y останется достаточно близким к какому-нибудь долгосрочному среднему значению.

Практические результаты.

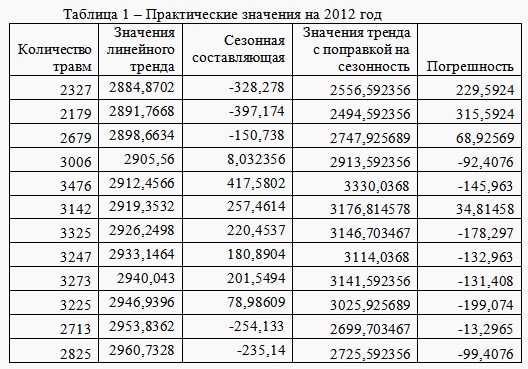
. На основании имеющихся данных были получены значения линейного тренда и сезонной составляющей. Затем были рассчитаны значения тренда с поправкой на сезонность. Графическое представление полученных результатов представлено на рис. 1.

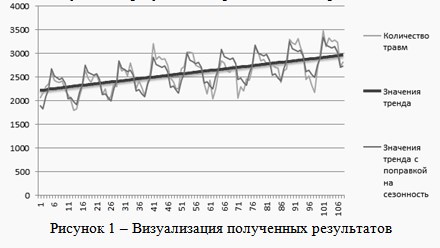
В качестве проверочных значений для оценки качества прогноза были выбраны данные за 2012 год.

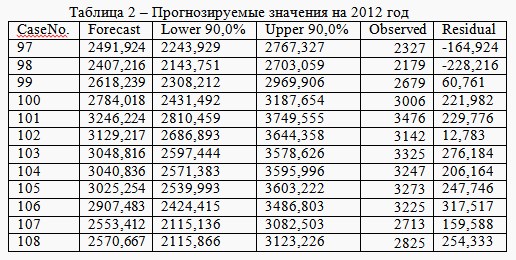
Результаты применения метода ARIMA представлены в табл. 2 в виде числовых значений и на рис. 2 в виде графического представления практических и прогнозируемых данных.

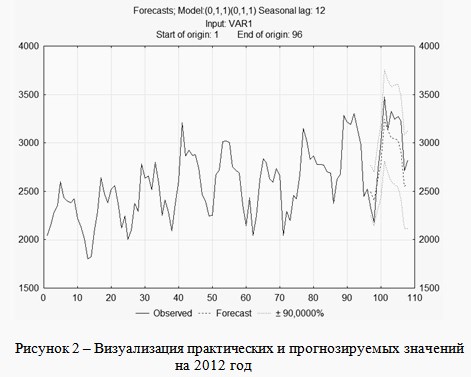
Выводы.

Произведен анализ имеющихся данных. На их основании получены значения линейного тренда и сезонной составляющей. Рассчитаны значения тренда с поправкой но сезонность. Получены прогнозируемые результаты. Анализ полученных данных и визуальная оценка позволяют судить о правильности полученных результатов.

Список литературы

Сигел Э. Практическая бизнес-статистика.: Пер. с англ. – М.: Издательский дом «Вильямс», 2002. – 1056 с.
Афанасьев В.Н. Эконометрика в пакете STATISTICA: учебное пособие по выполнению лабораторных работ / В.Н. Афанасьев, А.П. Цыпин, - Оренбург: ГОУ ОГУ, 2008. – 204с.
Кильдышев, Г.С., Френкель, А.А. Анализ временных рядов и прогнозирование. – М.: Статистика. 1973.
Боровиков, В.П. STATISTICS. Искусство анализа данных на компьютере : Дин профессионалов 2-е изд (+CD) – СПб.: Питер. 2003. – 668 с.