Исследование принципов формирования образующих множеств при построении взвешенной обучающей выборки w-объектов
Автор: Семенова А.П., Волченко Е.В.
Источник: Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС-2014) / Матерiали V мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2014. – С. 464–469.
Аннотация
Семенова А.П., Волченко Е.В. Исследование принципов формирования образующих множеств при построении взвешенной обучающей выборки w-объектов. В работе рассматривается проблема формирования эффективных обучающих выборок в адаптивных системах распознавания. Проводится анализ особенностей построения образующих множеств с точки зрения выбора начальных точек. Приведены результаты экспериментальных исследований, подтверждающие влияние выбора начальных точек на формирование получаемых выборок w-объектов.
Постановка проблемы и анализ литературы
Системы распознавания находят все большую область применения в повседневной жизни. Это связано с разработкой большого количества разнообразных устройств (систем технической и медицинской диагностики, компьютеров, охранных систем, «спам»-фильтров электронной корреспонденции, роботов, и т.д.), автоматическая работа которых невозможна без распознавания текущего состояния объектов, процессов и состояний, с которыми эти устройства работают.
Большинство современных прикладных задач, решаемых путем построения систем распознавания, характеризуется большим объемом исходных данных и возможностью добавления новых данных уже в процессе работы систем. Именно поэтому основными требованиями, предъявляемыми к современным системам распознавания, являются:
– адаптивность, состоящая в возможности системы в процессе работы изменять свои характеристики (для обучающихся систем распознавания – корректировать решающие правила классификации) при изменении окружающей среды (добавлении новых объектов обучающей выборки);
– работа в реальном времени, предполагающая наличие возможности формирования решений о классификации за ограниченное время;
– высокая эффективность классификации для линейно разделимых и пересекающихся в признаковом пространстве классов [1,4].
Информация об изменении распознаваемых объектов поступает в системы распознавания в большинстве случаев в виде новых объектов обучающей выборки. Количество объектов в обучающей выборке может достигать десятков тысяч, поэтому для адаптивных систем одной из ключевых проблем является проблема предобработки исходных выборок данных. Предобработка данных включает в себя очистку данных (удаление шума и пропусков в данных), сжатие и объединение данных.
Для сокращения размера выборок существуют различные алгоритмы, но они имеют ряд недостатков. Такие алгоритмы как STOLP, ДРЭД просты в реализации, но дают большую погрешность при решении задач с большим объемом входных данных, алгоритм NNDE практически не приспособлен для решения таких задач [2,5].
Метод построения взвешенной выборки w-объектов
В работе [3] предложен метод построения взвешенной обучающей выборки w-объектов для сокращения выборок большого объема в адаптивных системах распознавания.
Основой данного метода является выбор множеств близкорасположенных объектов исходной выборки и их замена одним взвешенным объектом новой выборки. Значения признаков каждого объекта новой выборки являются центрами масс значений признаков объектов исходной выборки, которые он заменяет. Введенный дополнительный параметр – вес определяется как количество объектов исходной выборки, которые были заменены одним объектом новой выборки.
Предлагаемый метод ориентирован как на сокращение исходной обучающей выборки, так и на анализ необходимости корректировки выборки и быстрое выполнение такой корректировки при пополнении выборки в процессе работы системы.
Построение w-объекта состоит из трех последовательных этапов:
1) построение образующего множества Wf, содержащее некоторое количество d объектов исходной выборки, принадлежащих одному классу;
2) формирование вектора Xi W = {xi1, xi2,...,xin}, значений признаков w-объекта Xi W и расчет его веса pi;
3) корректировка исходной обучающей выборки – удаление объектов, включенных в образующее множество X = X \Wf.
Построение образующего множества Wf состоит в нахождении начальной точки Xf1 формирования w-объекта, определении конкурирующей точки Xf2 и выборе в образующем множестве Wf таких объектов исходной выборки, расстояние до каждого из которых от начальной точки меньше, чем расстояние от них до конкурирующей точки. В качестве начальной точки Xf1 формирования w-объекта используется объект исходной обучающей выборки, наиболее удаленный от всех объектов других классов. Конкурирующая точка Xf2 выбирается путем нахождения ближайшего к Xf1 объекта, не принадлежащего тому же классу, что и сам Xf1, т.е. yf1 ≠ yf2.
Для случая двух классов выбор объектов {Xf1,Xf2,...,Xd} образующего множества Wf осуществляется по следующему правилу: Xi включается в Wf, если:
– он принадлежит тому же классу, что и начальная точка Xf1;
– расстояние от рассматриваемого объекта до начальной точки Xf1 меньше, чем до конкурирующей точки Xf2;
– расстояние Ri,1 от рассматриваемого объекта до начальной точки меньше расстояния Ri,2 от рассматриваемого объекта до конкурирующей точки и меньше расстояния R1,2 между начальной и конкурирующей точками (для случая, когда классы состоят из нескольких отдельных областей признакового пространства).
Таким образом, образующее множество Wf формируется по правилу:
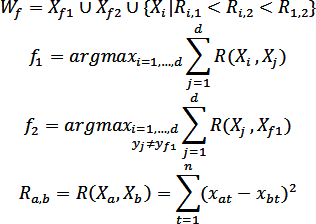
Значения признаков {xi1,xi2,...,xin} нового w-объекта XiW формируются по образующему множеству Wf и рассчитываются как координаты центра масс системы из pf = |Wf |материальных точек (примем, что объекты исходной обучающей выборки, являющиеся в признаковом пространстве материальными точками, имеют массу, равную 1), где |Wf | – мощность множества Wf, т.е.
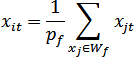
После формирования очередного w-объекта, все объекты образующего его множества удаляются из исходной обучающей выборки, т.е. X=X\Wf. Алгоритм заканчивает свою работу, когда в исходной обучающей выборке не останется ни одного объекта X∈∅.
Целью написания данной статьи является проведение анализа особенностей построения образующих множеств с точки зрения выбора начальных точек.
Исследование принципов формирования образующих множеств
Рассмотрим особенности построения образующих множеств на примере объектов двух классов. На рис. 1 приведен результат работы метода построения взвешенной обучающей выборки w-объектов, в котором начальной точкой является объект исходной обучающей выборки наиболее удаленный от всех объектов другого класса.

Рисунок 1 – Результат формирования w-объектов с наиболее удаленной начальной точкой
Как видно из рисунка, используя такой подход к формированию взвешенной обучающей выборки w-объектов можно существенно сократить размер исходной выборки (в данном примере размер обучающей выборки был сокращен с 70 объектов до 18).
Рассмотрим случай, когда в качестве начальной точки может быть выбран любой объект исходной обучающей выборки независимо от расположения среди объектов своего и противоположного классов.
На рис. 2 приведены варианты формирования образующих множеств для построения выборки w-объектов при условии, что начальной точкой может быть любой объект исходной обучающей выборки.
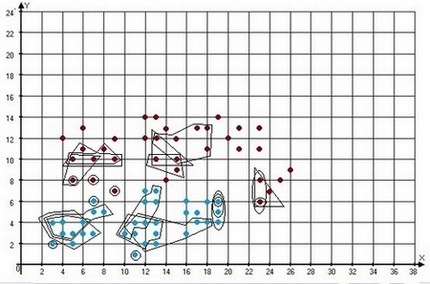
Рисунок 2 – Варианты формирования w-объектов со случайными начальными точками
На рис. 2 расположение объектов исходной обучающей выборки идентично расположению объектов на рис. 1. При выборе начальной точки в случайном порядке, можно увидеть, что от этого выбора зависит размер образующего множества (количество объектов, которые будут заменены одним w-объектом, т.е. вес w-объекта), вектор значений признаков w-объекта и, соответственно, качество и скорость распознавания. Отчетливо видно, что некоторые объекты могут быть включены в различные образующие множества, а некоторые могут не входить ни в одно из них. Объекты, которые формируют образующее множество из самих себя, расположены близко к объектам противоположного класса или являются максимально удаленными объектами от объектов противоположного класса.
Таким образом, в результате проведенного исследования принципов формирования образующих множеств при построения взвешенной обучающей выборки w-объектов было получено следующее:
– от выбора начальной точки зависит количество объектов, входящих в образующее множество и, соответственно, количество w-объектов;
– eсли объект исходной обучающей выборки, наиболее удаленный от всех объектов другого класса, не выбирается в качестве начальной точки, то он не входит в образующее множество и не заменяется на w-объект;
– существуют объекты, назовем их неустойчивыми объектами, которые могут входить во все возможные образующие множества;
– существуют объекты, назовем их условно устойчивыми объектами, которые входят более чем в половину возможных образующих множеств;
– в качестве начальной точки нельзя выбирать объекты близко расположенные к объектам другого класса, так как в этом случае образующее множество формируется только из начальной точки или из такого количества объектов, замена которых на w-объект не является целесообразной.
Выводы
Результаты исследования говорят о том, что выбор объекта, наиболее удаленного от всех объектов другого класса, в качестве начальной точки является эффективным способом сокращения размера исходной выборки, но может привести к неточностям в распознавании. Необходимо учитывать, что неустойчивые и условно устойчивые объекты могут привести к ошибкам классификации, так как могут включаться в различные образующие множества и, соответственно, формировать w-объекты с различными векторами значений признаков. Поэтому целесообразно формировать два обязательных типа образующих множеств. В первый тип множеств будут включены все неустойчивые объекты, а во второй – условно устойчивые объекты.
Список использованной литературы
1. Pal S.K. Pattern Recognition Algorithms for Data Mining: Scalability, Knowledge Discovery and Soft Granular Computing / S.K. Pal, P. Mitra – Chapman and Hall/CRC, 2004. – 280 p.
2. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. – Новосибирск: ИМ СО РАН, 1999. – 270 с.
3. Волченко Е.В. Метод построения взвешенных обучающих выборок в открытых системах распознавания // Доклады 14-й Всероссийской конференции "Математические методы распознавания образов (ММРО-14)", Суздаль, 2009. – М.: Макс-Пресс, 2009. – С. 100–104.
4. Александров А.Г. Оптимальные и адаптивные системы / А.Г. Александров – М.: Высшая школа, 1989. – 263 с.
5. Потапов А.С. Распознавание образов и машинное восприятие. – СПб.: Политехника, 2007. – 548 с.