Сеточный подход к построению взвешенных обучающих выборок w-объектов в адаптивных системах распознавания

Аннотация

Волченко Е.В. – Сеточный подход к построению взвешенных обучающих выборок w-объектов в адаптивных системах распознавания. В работе рассматривается проблема формирования эффективных обучающих выборок в адаптивных системах распознавания. Предложен метод построения взвешенных выборок w-объектов на основе сеточного подхода. Выполнена оценка предложенного метода, доказана его сходимость и вычислена временная сложность. Приведены результаты экспериментальных исследований, подтверждающие высокое качество получаемых выборок w-объектов.

Ключевые слова: адаптивная система распознавания, w-объект, обучающая выборка, сеточный подход.

Постановка проблемы и анализ литературы

Постоянно увеличивающийся объем информации, скорость изменения объектов и процессов, происходящих в окружающем мире, требует разработки подходов, позволяющих адаптировать автоматические системы к таким изменениям. Данная проблема является одной из наиболее актуальных в современной теории построения систем распознавания [1].

Современные системы распознавания должны не только обеспечивать эффективность классификации объектов по исходным данным, но и отвечать требованиям адаптивности и работы в режиме реального времени [2, 3]. Под адаптивностью принято понимать [2] способность системы изменять свои свойства (словарь признаков, обучающую выборку, решающие правила классификации и т. д.) в соответствии с изменениями распознаваемых объектов. Работа в реальном времени требует построения решающих правил, позволяющих принять решение о классификации за выделенное время [3].

Информация об изменении распознаваемых объектов поступает в системы распознавания в большинстве случаев в виде новых объектов обучающей выборки, количество которых может достигать десятков тысяч, поэтому для адаптивных систем одной из ключевых проблем является проблема предобработки исходных выборок данных.

Предобработка данных в системах распознавания является итеративным процессом и включает:

1) очистку данных, которая заключается в удалении шума, пропусков в данных и данных низкого качества [1];

2) сжатие данных, включающее нахождение минимального признакового пространства и репрезентативного множества данных на основе методов редукции и трансформации [2];

3) объединение данных, позволяющее уменьшить объем данных с сохранением исходной информации с помощью эвристических алгоритмов [1, 3].

Задача сжатия данных при условии неизменяющегося словаря признаков может быть решена двумя способами. Первый способ заключается в отборе некоторого множества объектов исходной обучающей выборки, каждый из которых отвечает предъявляемым требованиям. Наиболее известными алгоритмами, реализующими такой способ, являются алгоритмы STOLP [4], FRiS-STOLP [5], NNDE (Nearest Neighbor Density Estimate) и MDCA (Multiscale Data Condensation Algorithm) [1]. Основными отличиями этих алгоритмов друг от друга являются способ отбора объектов, используемое расстояние и критерий оптимальности полученной выборки. Второй способ состоит в построении множества новых объектов, каждый из которых строится по информации о некотором подмножестве объектов исходной обучающей выборки и обобщает его. Основой алгоритмов данного типа является дискретизация пространства признаков и анализ полученных частей пространства независимо друг от друга [6]. К алгоритмам такого типа можно отнести, например, алгоритм ДРЭТ [4], покрывающий признаковое пространство множеством пересекающихся окружностей, определяя тем самым области, принадлежащие каждому из классов.

Одним из перспективных подходов данного направления является наложение на пространство признаков некоторой «решетки», делящей все пространство на прямоугольные области, называемые в дальнейшем клетками. К алгоритмам, реализующим такой подход, относятся алгоритмы LVQ (learning vector quantization) [6], алгоритм четкого разбиения пространства признаков [7], алгоритм GridDC [8]. Основным отличием алгоритма GridDC от двух других является формирование на выходе новой сокращенной обучающей выборки, а не множества классифицированных клеток, являющихся одновременно и решающим правилом классификации. Недостатком формирования классифицированных клеток является то, что получаемое разбиение в большинстве случаев очень грубо аппроксимирует границы классов и может оказаться как чрезмерно избыточным, так и крайне недостаточным по числу выделенных клеток [8]. Формирование выборки объектов позволяет использовать для построения решающих правил известные алгоритмы, дающие более эффективные решения классификации.

В предыдущих работах автора, например в [9], была предложена идея перехода к взвешенным сокращенным выборкам w-объектов, имеющим кроме значений признаков дополнительный параметр – вес. Вес содержит информацию о взаиморасположении, количестве или качестве заменяемых объектов и, исходя из результатов экспериментальных исследований, проведенных в предыдущих работах, позволяет существенно повысить эффективность работы систем.

Данная работа является обобщением и развитием идей, предложенных автором в работах [8, 10, 11] и посвящена разработке метода построения взвешенных выборок w-объектов на основе сеточного подхода в адаптивных обучающихся системах распознавания.

Цель статьи

Цулью статьи является разработка метода построения взвешенной обучающей выборки w-объектов на основе сеточного подхода по исходной выборке и при добавлении новых обучающих объектов в процессе работы системы.

Постановка задачи

В качестве исходных данных дано некоторое множество объектов X={X₁,Х₂,...,Х_k}, представленное в виде объединения непересекающихся классов 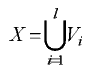и называемое обучающей выборкой. Каждый объект X_i из X описывается системой признаков, т. е. X_i={X_i1,X_i2,...,X_in} и представляется точкой в линейном пространстве признаков, т. е. X_i∈Rⁿ. Для каждого объекта X_i известна его классификация y_i∈[1,l].

Определение 1. Качеством классификации N(Z,X) / |Z| назовем частоту неверной классификации объектов контрольной выборки Z решающим правилом, построенным по исходной обучающей выборке X.

Через |Х| будем определять мощность множества X т. е. количество объектов, принадлежащих этому множеству.

Необходимо сформировать классифицированную взвешенную обучающую выборку w-объектов X^W={X₁^W,X₂^W,...,X_m^W}, y_i^W∈[1,l], где X^W={X_i1^W,X_i2^W,...,X_in^W,p_i}, p_i – вес i-го w-объекта.

Построенная выборка w-объектов должна отвечать следующим требованиям:

а) размер выборки w-объектов должен быть меньше размера исходной обучающей выборки |X|<|X^W|;

б) каждый объект новой выборки (w-объект) должен относиться к тому же классу, что и объекты, по которым он сформирован;

в) качество классификации N(Z,X^W) / |Z| решающим правилом, построенным по выборке w-объектов, должно удовлетворять неравенству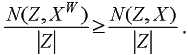

Построение выборки w-объектов по исходной обучающей выборке на основе алгоритма GridDC

Идеей метода GridDC [8] является наложение сетки на признаковое пространство для формирования множества клеток, определение объектов выборки, принадлежащих каждой из клеток, и их замена на w-объекты. Формирование объектов новой выборки выполняется только в случае принадлежности всех объектов клетки одному классу. Вес w-объектов определяется по количеству объектов исходной выборки, принадлежащих клетке.

Далее приведем пошаговое описание метода. Без потери общности получаемых решений применим стандартный для теории распознавания подход, заключающийся в рассмотрении двухклассовых систем.

Шаг 1. Формирование сетки. Рассчитывается шаг клетки s по формуле:

где [...] – оператор округления до ближайшего целого значения; mах{х_i} – максимальное значение i-го признака среди всех объектов выборки, min{x_i} – минимальное значение.

Выполняется разбиение признакового пространства Rⁿ по каждому из п признаков на интервалы длиной s (наложение прямоугольной сетки), результатом которого является множество клеток G. Далее для каждого объекта выборки X определяется клетка, которой этот объект принадлежит.

Утверждение 1. Объект Х_i принадлежит некоторой клетке G_j тогда и только тогда, когда каждое из значений его признаков входит в интервал значений соответствующих признаков данной клетки.

В результате формирования сетки и обработки объектов исходной обучающей выборки будут сформированы непересекающиеся подмножества Х_Gj объектов, принадлежащих клетке G_j, j∈[1,|G|].

Шаг 2. Формирование значений признаков w-объектов. Возможны следующие варианты обработки содержимого клеток.

1. Если все объекты клетки принадлежат к одному классу, то значения признаков объекта новой выборки рассчитываются как координаты центра масс объектов этой клетки:

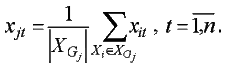
2. Если клетка не содержит ни одного объекта, то объект новой выборки не формируется.

3. Если клетка содержит объекты нескольких классов, то она делится на две равные по размеру клетки (поочередно вертикально или горизонтально) до тех пор, пока любая из клеток внутри начальной клетки не будет содержать объекты только одного класса. Далее по каждой из полученных клеток формируются объекты новой выборки (согласно случаям 1 и 2).

Классификация w-объекта определяется по классификации объектов, по которым он сформирован.

Шаг 3. Определение веса w-объектов. Вес w-объекта равен количеству объектов исходной выборки, принадлежащих клетке, т. е. p_j=|Х_Gj|.

В результате выполнения алгоритма будет получена новая взвешенная обучающая выборка w-объектов Х^W.

Пополнение взвешенной обучающей выборки w-объектов

Задачу пополнения выборки w-объектов новыми обучающими объектами целесообразно рассматривать относительно только одного некоторого объекта Х_а={х_а1,х_а2,...,х_аn}, набор признаков которого совпадает с набором признаков объектов исходной выборки, поскольку новые обучающие объекты поступают в систему распознавания последовательно и обрабатываются аналогично. Для решения задачи пополнения обучающей выборки w-объектов новыми классифицированными объектами в процессе работы системы на основе сеточного подхода предлагается следующий алгоритм.

Шаг 1. Определяется клетка, которой принадлежит добавляемый объект X_а.

Шаг 2. Выполняется корректировка существующего или построение нового w-объекта, соответствующего найденной клетке.

Если найденный w-объект относится к тому же классу, что и добавляемый объект, то вес w-объекта увеличивается на единицу и значения его признаков пересчитываются:

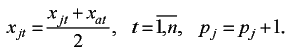
2. Если найденной клетке не соответствует ни один w-объект (т.е. ни один объект исходной выборки или добавленный ранее не принадлежал этой клетке), то формируется новый w-объект со значениями признаков, равными значениям признаков добавляемого объекта, и единичным весом:

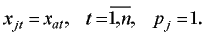
3. Если классификация найденного w-объекта не совпадает с классификацией добавляемого объекта, то выполняется деление этой клетки на две равные по размеру клетки (поочередно вертикально или горизонтально), как и при построении w-объектов по исходной выборке, до тех пор, пока все построенные клетки не будут содержать объекты только одного класса.

Далее по каждой из полученных клеток формируются w-объекты по следующим правилам.

Если клетка содержит только добавляемый объект X_а, то построение w-объекта аналогично случаю 2 данного алгоритма.

Для остальных полученных клеток формируются w-объекты со значениями признаков, равными центрам этих клеток и весом пропорционально количеству построенных клеток, т.е.

где q – количество клеток, полученных после разбиения исходной клетки.

Отметим, что разбиение клетки на две равные клетки вне зависимости от количества объектов в этой клетке, принадлежащих разным классам не влияет на эффективность работы систем распознавания, поскольку при построении решающих правил учитывается вес w-объектов.

Оценка метода построения выборки w-объектов на основе сеточного подхода

Анализ предложенного метода и обучающей выборки w-объектов позволяет сформулировать следующие утверждения.

Утверждение 2. Выборка w-объектов формируется по всем объектам исходной выборки.

Утверждение 3. Никакие два и более w-объектов не строятся по одному и тому же объекту исходной выборки.

Утверждение 4. W-объект принадлежит тому же классу, что и объекты исходной выборки, по которым он сформирован. Количество классов выборки w-объектов равно количеству классов объектов исходной выборки.

Утверждение 5. Вес w-объекта является целым числом и принимает значения от 1 до количества объектов |V_j| некоторого класса j.

Доказательство корректности данных утверждений непосредственно следует из имеющихся исходных данных и предложенных алгоритмов.

Теорема 1. Алгоритм построения выборки w-объектов сходится и его временная сложность равна O(klogk).

Доказательство. Основными элементами, обрабатываемыми в предложенных алгоритмах, являются множества обучающих объектов, принадлежащих клеткам. Количество клеток, на которые разбивается n-мерное признаковое пространство равно

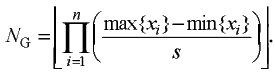
Обработка клеток проводится до тех пор, пока каждая клетка, полученная путем разбиения исходной, не будет содержать объекты только одного класса. Поскольку, согласно постановке задачи, никакие два объекта обучающей выборки не могут иметь одинаковые значения всех признаков и принадлежать разным классам, количество разбиений клеток конечно. Следовательно, алгоритм сходится за конечное число шагов.

Рассчитаем временную сложность алгоритма построения выборки w-объектов по исходной выборке. За единицу примем время обработки одного объекта исходной выборки.

На первом шаге алгоритма для расчета шага клетки выполняется поиск минимальных и максимальных значений признаков объектов, что требует nk итераций.

На втором шаге определяется принадлежность объектов клеткам, что требует k итераций.

На третьем шаге выполняется построение w-объектов по клеткам. При этом разбиение клеток для обеспечения однозначной классификации требует выполнения не более чем 2^|V_j| итераций.

Таким образом, временная сложность алгоритма построения выборки w-объектов по исходной выборке составляет nk + k + N_G^2|Vj| итераций. Если предположить, что каждая клетка содержит строго по одному объекту выборки, то N_G = k. Если предположить, что некоторая клетка содержит все объекты некоторого класса j, количество объектов которого близко размеру всей выборки, то 2^|V_j| ≈ 2^k. Следовательно, временная сложность алгоритма равна O(klogk).

Отметим, что временная сложность алгоритма пополнения взвешенной обучающей выборки w-объектов рассчитывается аналогично и также составляет O(klogk).

Результаты экспериментальных исследований

Для оценки эффективности предложенного метода был проведен ряд экспериментальных исследований. В качестве исходных данных были использованы сформированные по нормальному закону распределения выборки объектов двух классов размером 1000-5000 объектов, содержащих два признака распознавания. Степень пересечения классов в пространстве признаков изменялась от полной обособленности до пересечения на 40 %. В качестве решающего правила классификации по выборке w-объектов использовались модифицированный метод А-ближайших соседей [12] и модифицированный метод потенциальных функций [13]. Классификация объектов в модифицированном методе А-ближайших соседей определяется по к ближайшим w-объектам к распознаваемому объекту Х'={х₁,х₂,...,х_n} по следующей метрике:

где p_a = 1 - вес распознаваемого объекта, который принимается равным единице.
Два объекта являются ближайшими, если значение максимально. Объект X'_i относится к тому классу, объектов которого среди к ближайших больше.
Классификация объектов в модифицированном методе потенциальных функций выполняется с помощью решающего правила вида:

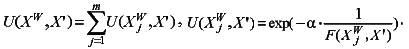
Анализ полученных результатов позволяет сделать следующие выводы:

1) частота неверной классификации объектов тестовой выборки методом k-ближайших соседей по выборке w-объектов на 7,4% меньше частоты неверной классификации методом А-ближайших соседей по исходной выборке и на 1,6 % меньше частоты неверной классификации методом потенциальных функций по исходной выборке;

2) время выполнения классификации предложенным методом на 3,8 % меньше времени классификации методом А-ближайших соседей по исходной выборке и на 37,9 % меньше времени классификации методом потенциальных функций по исходной выборке.

Анализ эффективности использования выборок w-объекгов, построенных по предложенному методу, для классификации объектов класса тестовых задач ADS 1 репозитория ISEC (International Statistical Education Centre) [14] показал уменьшение неверных классификаций по сравнению с классическими методами (методом k-ближайших соседей и методом потенциальных функций) в среднем на 3,4 %).
Также было получено, что из 100 добавляемых новых объектов только для 7 объектов потребовалось построение новых w-объектов, а для 4 - разделение существующих клеток.

Выводы

В работе предложен новый подход к построению взвешенных обучающих выборок w-объектов на основе сеточных алгоритмов в адаптивных системах распознавания. Описан метод формирования значений признаков w-объектов и их весов по исходной обучающей выборке и при добавлении в выборку новых обучающих объектов. Анализ предложенного метода показал его сходимость, низкую временную сложность, корректность обработки объектов исходной выборки. Результаты экспериментальных исследований показали уменьшение частоты неверных классификаций и времени её выполнения решающим правилом, построенным по выборке w-объектов, по сравнению с классическими методами.

Список использованной литературы

1. Larose D.T. Discovering knowledge in Data: An Introduction to Data Mining / D.T. Larose. – New Jersey, Wiley & Sons, 2005. – 224 p.
2. Pal S.K. Pattern Recognition Algorithms for Data Mining: Scalability, Knowledge Discovery and Soft Granular Computing / S.K. Pal, P. Ultra. – Chapman and Hall/CRC, 2004. – 280 p.
3. Olson D.L. Advanced Data Mining Techniques / D.L. Olson, D. Delen. – Springer-Verlag Berlin, 2008. – 180 p.
4. Загоруйко Н.Г. Прикладные методы анализа знаний и данных / Н.Г. Загоруйко. – Новосибирск: Издательство института математики, 1999. – 270 с.
5. Zagoruiko N.G. Methods of Recognition Based on the Function of Rival Similarity / N.G. Zagoruiko, I.A. Borisova, V.V. Dyubanov and O.A. Kutnenko // Pattern Recognition and Image Analysis. – 2008. – Vol. 18. – № 1. – P. 1–6.
6. Kohonen T. Self-Organizing Maps / T. Kohonen. – Springer-Verlag, 1995. – 501 p.
7. Субботин С.А. Метод обучения нейро-нечеткой сети распознаванию образов на основе прямоугольного разбиения пространства признаков / СА. Субботин II Складні системи i процеси. – 2009. – № 1. – С. 111–111.
8. Волненко Е.В. Метод сокращения обучающих выборок GridDC / Е.В. Волненко, И.В. Дрозд II Искусственный интеллект. – 2010. – № 4. – С. 185–190.
9. Волченко Е.В. Метод построения взвешенных обучающих выборок в открытых системах распознавания / Е.В. Волненко II Доклады 14-й Всероссийской конференции « Математические методы распознавания образов (ММРО-14)», Суздаль, 2009. – М.: Макс-Пресс, 2009. – С. 100–104.
10. Волченко Е.В. Пополнение взвешенных обучающих выборок w-объектов в адаптивных системах распознавания, построенных на основе сеточного подхода / Е.В. Волченко II Труды Международной научной конференции «Интеллектуальные системы принятия решений и проблемы вычислительного интеллекта (ISDMCr2011)». – Херсон: ХНТУ, 2011 – Том 2. – С. 205-209.
11. Волченко Е.В. Построение взвешенных обучающих выборок w-объектов на основе сеточного подхода / Е.В. Волченко II Доклады 15-й Всероссийской конференции «Математические методы распознавания образов (ММРО-15)», Петрозаводск, 2011. – М.: Макс-Пресс, 2011.
12. Волченко Е.В. Адаптация решающих правил в открытых системах распознавания / Е.В. Волченко II Тезисы докладов VII международной научно-практической конференции «Математическое и программное обеспечение интеллектуальных систем» (MPZIS-2009). – Днепропетровск, 2009. – С. 62–64.
13. Волченко Е.В. Модифицированный метод потенциальных функций / Е.В. Волченко II Бионика интеллекта. – 2006. – № 1 (64). – С. 86–92.
14. http://www.isical.ac.in/ – miu