Назад в библиотеку

---

Описание n log n алгоритма минимизации состояний в детерминированном конечном автомате

Автор: Yingjie XU

Перевод: Швец О.С.

Источник: Describing an n log n algorithm for minimizing states in deterministic finite automaton.

Аннотация

Существует несколько хорошо известных алгоритмов для минимизации детерминированных конечных автоматов. В данной работе приведен алгоритм предназначенный для минимизации конечного автомата или для определения эквивалентности двух конечных автоматов. Асимптотическое времени работы алгоритма ограничено с kn log n, где k–некоторая константа, которая линейно зависит от размера входного алфавита, и n–число состояний.

Содержание

1 Введение

2 Предварительные сведения

2.1 ДКА, слово и язык

2.2 Эквивалентные состояния и минимальный ДКА.

3 Минимизация

3.1 Классический алгоритм.

3.2 Алгоритм Хопкрофта

1 Введение

Проблема написания эффективных алгоритмов для нахождения минимального детерминированного конечного автомата, эквивалентного данному автомату может быть прослежена с 1950–х годов в работах Хаффмана[Huf55] и Мура[Moo58]. За это время были предложены альтернативные алгоритмы. Тем не менее, анализ этих алгоритмов указывал на то, что в худшем случае они имеют сложность n₂, где n–число состояний.

Хопкрофт [Hop71] в 1971 г. предложил алгоритм минимизации конечных детерминированных автоматов, сложности O(n log n) с n состояниями. Коэффициент пропорциональности линейно зависит от количества входных символов. Очевидно, что этот алгоритм может использоваться и для задачи определения, являются ли два конечных автомата эквивалентными. Последние исследования [BC04, BBC08] показали, что они тесно связаны.

Текст организован следующим образом. В разделе 2 мы приведем несколько определений и обозначений, используемых в данной статье. В разделе 3 мы опишем алгоритм Хопкрофта и объясним принцип его работы.

2 Предварительные сведения

2.1 ДКА, слово и язык

Определение 2.1. Детерминированный конечный автомат (ДКА) D задается пятеркой (Q, Σ, δ, q₀, F) где:

• Q – конечное множество состояний;
• Σ – входной алфавит;
• δ: Q×Σ → Q – функция переходов;
• q₀– начальное состояние;
• F ⊆ Q – множество заключительных состояний.

Если функция переходов всюду определена, то автомат D – называется полным.

Определение 2.2. Любая конечная последовательность символов алфавита a ∈ Σ – это слово.

Через Σ* обозначим множество всех слов в алфавите Σ и ε – пустое слово. Определим расширенную функцию перехода 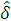: Q×Σ* → Q следующим образом:

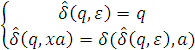
Определение 2.3. Язык, принимаемый автоматом D, L(D) – это множество всех слов w ∈ Σ* таких, что .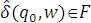

2.2 Эквивалентные состояния и минимальный ДКА

Для ДКА D = (Q, Σ, δ, q₀, F), два состояния q₁, q₂ Q называются эквивалентными и обозначаются q₁ ≈ q₂, если для любого w∈Σ*, 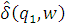∈F ↔ 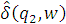∈F. Два состояния, которые не являются эквивалентными называются различимыми. Минимальный автомат D/≈, эквивалентный исходному, называется фактор–автоматом, и его состояния соответствуют классами эквивалентности ≈. Доказано, что он уникален с точностью до изоморфизма.

Определение 2.4. Два ДКА D и  эквивалентны, если и только если L(D) = L ().

Определению 2.5. ДКА называется минимальным, если нет другого эквивалентного ему ДКА, с меньшим числом состояний.

3 Минимизация

3.1 Классический алгоритм

Определение 3.1. Состояние q ∈ Q в ДКА D = (Q, Σ, δ, q₀, F) называется достижимым, если 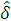(q₀,w) = q, для некоторого w ∈ Σ*.

Определение 3.2. Если все состояния, в Q достижимы, то полный ДКА D называется инициально связным (ИСДКА).

Лемма 3.1. Предположим, что D является ИСДКА. Тогда D – минимальный, если все пары состояний различимы.

Доказательство. (⇒) Это легко видеть, если D имеет два эквивалентных состояния. Тогда одно из них можно удалить, а дуги входящие в это состояние, можно перебросить в другое состояние. Это не повлияет на принимаемую последовательность.

(⇐) Предположим, что в D все состояния являются попарно различимы. Пусть D имеет k состояний. Рассмотреть любые другие  с l<k состояниями. Мы должны показать, что L() ≠ L(D).

Для каждого состояния q автомата D выберем произвольно одну строку w_q такую, что 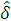(q₀,w_q) = q. Из предположения следует, что такое w_q существует для каждого q и все состояния являются достижимыми. Так как l < k, то существуют два состояния p ≠ q в D, такие, что в  мы имеем 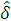(q₀,w_p) =  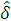(q₀,w_q). Поскольку p и q различимы в D, то существует последовательность w такая, что 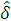(q_w) ∈ F, но 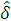(q_w) ∉ F (или наоборот, но если это так, то мы всегда можем поменять местами p и q). Это означает, что D принимает w_pw, но не w_qw. Но в  имеем 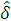(q₀,w_pw) = 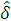(q₀,w_qw), так  либо принимает как w_pw так и w_qw, либо отвергает оба эти слова.

Поэтому L () ≠ L(D), что и требовалось.

Лемма 3.2. Состояние неразличимость является отношением эквивалентности.

Лемма 3.3. Пусть δ(p, a) = p′ и δ(q, a) = q′. Тогда, если p′, q′ различимые, то p, q также различимые.

Чтобы минимизировать автомат A, после удаления недостижимых состояний, мы отыщем все классы эквивалентности с неразличимыми состояниями и объединим их в одном состоянии нового автомата .

Чтобы определить, какие состояния являются эквивалентными, мы будем использовать следующий алгоритм. Вместо того чтобы пытаться выяснить, какие состояния неразличимы, мы постараемся выяснить, какие состояния различимы. Полный алгоритм приведен ниже.

Алгоритм 1. Классический алгоритм

Исходные данные: Детерминированный конечный автомат A

Результат: Минимальный автомат  эквивалентный А

1: Удалить недостижимые состояния

2: Отметить все пары p, q, где p ∈ F и q ∉ F

3:       repeat

4:             for всех неотмеченных пар p, q do

5:                   for всех символов a do

6:                             if пара δ(p, a), δ(q, a) отмечена then

7:                                     отметить p, q

8:                             end if

9:                   end for

10:        end for

11: until нет новых пар отмеченных состояний

12: Построить приведенный автомат

Теорема 3.1. Алгоритм минимизации 3.1 правилен, то есть L() = L(A) и  является минимальным.

Доказательство. Докажем все необходимые условия, одно за другим.

Эквивалентность выполняется. Доказательство легко проводится индукцией по длине кратчайшего слова, различающего p и q при помощи Леммы 3.3.

 корректно определен. Из того факта, что неразличимость является отношением эквивалентности по Лемме 3.2, следует, что состояния в определены корректно.

L() = L(A). Для каждого w имеем 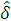(q₀,w) ∈ 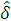(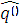,w).Таким образом, по определению заключительных состояний в , автомата  принимает w, если и только если A принимает w.

минимален. Здесь полезна Лемма 3.1. Это вполне очевидно следует из построения, при котором все состояния различимы.

Теорема 3.2. Время работы Алгоритма 3.1 составляет O(n²).

3.2 Алгоритм Хопкрофта

Лемма 3.4. Пусть D = (Q, Σ, δ, q₀, F) и последовательность ρ_i (i ³ 0) отношений эквивалентности на Q описывается следующим образом:

ρ₀ = {(p, q)|p, q ∈ F}, ∪ {(p, q)|p, q ∈ Q - F},

ρ_i+1 = {(p, q) ∈ ρ_i|(∀a ∈ Σ)(δ(p, a), δ(q, a)) ∈ ρ_i}.

Справедливы следующие утверждения:

• ρ₀ ⊇ ρ₁ ⊇ · · · .

• если ρ_i = ρ_i+1, то ρ_i = ρ_j для всех j > i.

• существует 0 ≤ k ≤ |Q| такой, что ρ_k = ρ_k+1.

Рассмотрим ситуацию, когда ρ_i ≠ ρ_i+1,

ρ_i ≠ ρ_i+1

↔ (∃p,q ∈ Q, a ∈ Σ)(p,q) ∈ ρ_i и (δ(p,a), δ(q,a)) ∉ ρ_i

↔ (∃U∈ Q/ρ_i, a ∈ Σ ) p,q ∈ U и (δ(p,a), δ(q,a)) ∉ ρ_i

↔ (∃U,V ∈ Q/ρ_i, a ∈Σ) p,q ∈ U и δ(p,a) ∈ V и δ(q, a) ∉ V (1)

↔ (∃U,V ∈ Q/ρ_i, a ∈ Σ) δ(U,a) ∩ V ≠ 0< и δ(U,a) ⊄ V

При помощи леммы 3.4, может быть построено отношение эквивалентности на D с помощью алгоритма, приведенного ниже:

Алгоритм 2. Вычисление эквивалентного отношения с помощью уточнения

1: Q/θ ← {F,Q - F}

2: while (∃U,V ∈ Q/θ, a ∈ Σ ) (см. соотношение 1) do

3:          Q/θ ← (Q/θ {U}) U {U ∩ δ^-1(V, a), U - U ∩ δ^-1(V, a)}

4: end while

Пока это довольно абстрактно, и, мы должны решить, как эффективно находить некоторые тройки U, V, a для которых выполняется соотношение 1.

Леммы 3.5. Пусть D = (Q, Σ, δ, q₀, F) и U принадлежат Q/θ. Предположим, что мы разобьем U на U′ и U′′. Тогда для любого a из Σ, разбиение всех классов θ, относительно (U′, a) и (U′′, a) дает тот же результат, как и разбиение θ относительно (U, a), (U′, a) и (U′′, a).

Леммы 3.6. Пусть D = (Q, Σ, δ, q₀, F), Q/θ = {F,Q - F}, a из Σ. Тогда разбиение θ относительно либо (F, a) или (Q – F, a) дает тот же результат, как и разбиение θ относительно их обоих.

Алгоритм 3. Алгоритм Хопкрофта

1: W ← {F,Q − F}

2: W ← {F,Q − F}

3: W  – не пустое do

4:          выберите и удалите S с W

5:                   for all a из K do

6:                            l_a ← δ⁻¹(S, a)

7:                             for all R иP таких, что R ∩ l_a ≠ ∅ and R ⊄ l_a do

8:                                      раздел R в R1 and R2: R1 ← R ∩ l_a and R2 ←R − R1

9:                             заменить R в Р с R1 и R2

10:                           if R ∈ W then

11:                                    заменить R в W, в R1 и R2

12:                           else

13:                                    if |R1| W |R2| then

14:                                             добавить R1 в W

15:                                    else

16:                                             добавить R2 в W

17:                                    end if

18:                           end if

19:                 end for

20:        end for

21: end while

Леммы 3.5 и 3.6 предоставили возможность сократить вычисления. Алгоритм 3.2 – алгоритм Хопкрофта:

Теорема 3.3. Пусть U = {U₁,U₂, . . . Х_m} (1 ≤ m ≤ |Q|) – множество всех построенных классов, созданных алгоритмом минимизации. Тогда

Теоремы 3.4. Время работы алгоритма 3.2 составляет O(n log n).

Ссылки

[BBC08] Jean Berstel, Luc Boasson, and Olivier Carton. Hopcroft's automaton minimization algorithm and sturmian words. In DMTCS'2008, volume AI, pages 355–366, 2008.

[BC04] Jean Berstel and Olivier Carton. On the complexity of hopcroft's state minimization algorithm. In CIAA'2004, volume 3317, pages 35–44, 2004.

[Hop71] J.E. Hopcroft. An n log n algorithm for minimizing states in a _nite automaton. Technical Report CS–71–190, Stanford University, January 1971.

[Huf55] D.A. Hu_man. The synthesis of sequential switching circuits. The Journal of Symbolic Logic, 20(1), 1955.

[Moo58] E.F. Moore. Gedanken–experiments on sequential machines. TheJournal of Symbolic Logic, 23(1), 1958.