Умови збереження поведінки автомата при двох перекидах дуг

Автор:О.М. Копитова
Джерело: Материалы IV международной научно–практической конференции Образование и наука без границ–2008. Польша, Перемышль. – 2008. – Т. 17. – С. 33–37.

Вступ

Сучасні інформаційні технології спираються значною мірою на теоретичний фундамент дискретної математики і математичної кібернетики. Однією з базових математичних моделей цих теорій є модель скінченного автомата. Ця модель є корисною для опису інформаційної взаємодії об’єктів різноманітної природи, починаючи від технічних, пов’язаних з задачами побудови керуючих систем, і до таких, як соціальні групи, що взаємодіють між собою, обмінюючись інформацією в залежності від їх стану та впливу зовнішнього середовища. Виникають моделі поведінки таких об’єктів, основними характеристиками яких є поняття стану, вхідного стимулу і реакції на нього.

Складні системи, що досліджуються протягом свого життєвого циклу, можуть міняти свою структуру під впливом з боку середовища. При цьому поведінка нової системи може або відрізнятися від поведінки старої, або залишатися без зміни, незважаючи на те, що структура системи зазнала змін. Умови, за якими зберігається поведінка системи, певним чином характеризують її стійкість до деформуючих впливів зовнішнього середовища.

Таким чином, виникає задача вивчення таких структурних змін, за яких поведінка нової системи не змінюється у порівнянні зі старою. Формалізація відповідної задачі може бути виконана у рамках теорії автоматів.

Дослідження поведінки автоматів, які породжуються один з одного за допомогою перекидів дуг, мають вже досить давню історію. Але отримані до цього часу результати не дозволяють стверджувати, що ця задача добре вивчена. В основному вона розглядалася в рамках теорії експериментів з автоматами [1]. Споріднені задачі розглядалися у теорії графів, де вивчалася задача визначення, коли один з графів (автомат) може бути отримано з іншого деякою послідовністю перекидів дуг [2]. Вплив перекидів дуг на поведінку автомата вивчався пізніше у роботах [3, 4]. Було доведено, що перекид тільки однієї дуги завжди викликає зміну поведінки – автомат стає нееквівалентним заданому приведеному автомату [4]. У доповіді доведено, що перекид вже двох дуг принципово змінює ситуацію.

1. Формальна постановка задачи

Основні визначення теорії автоматів можна знайти в [5].

П’ятірка (А,Х,Y,f,g) називається автоматом Мілі, якщо вона складається із множини станів автомата А, множини вхідних символів Х, множини вихідних символів Y, функції переходів f: А × Х → А і функції виходів g: А × Х → Y. Множини Х і Y називають відповідно вхідним і вихідним алфавітами автомата. Будемо позначати автомат символом множини його станів, тобто А=(А,Х,Y,f,g). Автомат А будемо розглядати також як множину дуг, де дуга – це четвірка (s,x/y,t), якщо f(s,x)=t, g(s,x)=y.

Два стани а i b одного i того ж автомата А , чи двох різних автоматів А і В називаються еквівалентними, якщо для всякого вхідного слова р виконується f(a,p) = f'(b,p), де f' – функція виходів автомата А або В [5]. Автомат називається приведеним, якщо всі його стани попарно нееквівалентні [5].

Надалі розглядатимемо автомати А і В, у яких вхідні i вихідні алфавіти збігаються, тобто А = (А, Х, Y, f, g) i В = (В, Х, Y, f', g'). У цьому випадку відображення z: А→B буде називатися гомоморфізмом автомата А в автомат B, якщо для кожних а∈А і х∈Х:

1) z(f(a,x)) =f'(z(a),x);

2) g(а, х) = g'(z(a),x).

Гомоморфізм z називається ізоморфізмом, якщо z – взаємно однозначний гомоморфізм [5].

Нехай А = (А, Х, Y, f, g) – приведений автомат. Нехай також автомат В є результатом перекидання деяких двох дуг в автоматі А: наприклад, дуга (s, x/y, s₁) перекидається у стан s₂, тобто замінюється дугою (s, x/y, s₂), а дуга(t, x′/y′, t₁) перекидається у стан t₂, тобто замінюється дугою (t, x′/y′, t₂).

Задача полягає в тому, щоб визначити умови, за яких автомат В залишається ізоморфним заданому автомату А.

Приклади збереження поведінки

Легко навести приклади, коли результатом перекиду в автоматі двох дуг є новий автомат, не ізоморфний вихідному.

Розглянемо протилежні приклади – коли перекиди двох дуг в автоматі призводять до автомата, ізоморфного заданому.

На малюнку 1 наведено граф переходів приведеного автомата А, а на малюнку 2 – автомата В, який є результатом перекидання двох дуг в автоматі А: дуга (s,1/0,4) перекидається у стан 3, тобто замінюється дугою (s,1/0,3), а дуга (t,1/0,3) перекидається у стан 4, тобто замінюється дугою (t,1/0,4). Легко бачити, що відображення z: А→B, таке, що:

z(1)=2; z(2)=1; z(s)=t; z(t)=s; z(3)=3; z(4)=4,

реалізує ізоморфізм автомата А на автомат В. Це означає, що автомат В також приведений і еквівалентний автомату А.

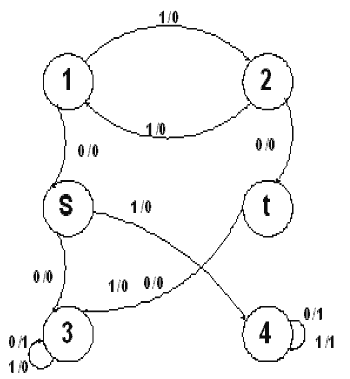
Мал.1. Автомат А

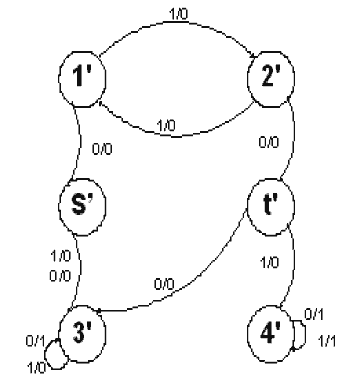
Мал.2. Автомат В

Відмітимо особливості структури автомата А. В ньому є два нееквівалентні стани 3 та 4, в які спрямовано з двох різних станів s і t дуги, що перекидаються. З станів 3, 4 стани s і t досягти не можна. Ті стани, з яких досягаються s і t , можна розбити на такі пари, з яких стани s і t досягаються по однакових словах. Цим словам відповідають такі послідовності дуг графа переходів, які не включають дуг, що перекидаються. Елементи всіх таких пар, включаючи s і t, відображаються z один в одне. Інші стани відображаються самі в себе.

Подібні особливості структури далі сформулюємо як умови, за яких зберігається поведінка автомата при двох перекидах його дуг.

Достатні умови збереження поведінки

На підставі наведених прикладів визначимо достатні умови, що накладаються на структуру заданого автомата для того, щоб зберігалася поведінка автомата при перекидах двох його дуг.

Нехай А = (А, Х, Y, f, g) – приведений автомат. Через K(A) позначимо множину всіх станів автомата А, які входять до сильно зв’язних підавтоматів автомата А.

Припустимо, що s і t є такі стани автомата А, які не належать K(A) і задовольняють наступним умовам:

для кожного вхідного символу х∈ Х виконується рівність g(s, x)=g(t, x);
існує вхідний символ х′ ∈ Х, для якого f(s, x′) і f(t, x′) – різні і належать K(A);
для усіх інших вхідних символів х ≠ x′, якщо f(s, x) = f(t, x), то f(s, x) належить K(A);
якщо х ≠ x′ та f(s, x) ≠ f(t, x), то або одночасно f(s,x) = t і f(t,x) = s, або одночасно f(s, x) = s і f(t, x) = t.

Такі стани s і t назвемо перспективними, а дуги (s, x′/y, s₁), (t, x′/y, t₁) назвемо виділеними дугами перспективних станів, де y=g(s, x′), s₁=f(s, x′), t₁=f(t, x′).

Станам s і t поставимо у відповідність множину станів Ф, з яких можна досягти або s або t . Вважатимемо, що s, t ∈ Ф.

Назвемо пару перспективних станів s і t допустимою, якщо відповідну їм множину Ф можна розбити на такі дві рівнопотужні множини Ф_s и Ф_t, що не перетинаються, s ∈ Ф_s і t ∈ Ф_t, і для яких існує взаємно однозначне відображення φ : Ф_s ↔ Ф_t, що задовольняє умовам:

Для кожного r_s ∈ Ф_s існує r_t ∈ Ф_t такий, що φ(r_s) = r_t і навпаки, для кожного r_t ∈ Ф_t існує r_s ∈ Ф_s такий, що φ(r_s) = r_t, причому φ(s) = t, φ(t) = s;
Для кожного r ∈ Ф_a, де a=s або a=t, i кожного вхідного слова p виконується:

якщо f(r, p)=a′, де a′= s або a′= t, то f(φ(r), p) =φ(а′) і g(r,p)=g(φ(r), p).

Кожному вхідному слову p і стану a∈ A в графі переходів автомата А відповідає шлях, який починається в стані а і включає деяку множину дуг U_p графа переходів. Будемо казати, що дуга u ∈ U_p покривається словом p із стану a.

З визначень перспективних і допустимих станів випливають два твердження.

Твердження 1. Ф_a ∩ K(A) = ∅, якщо а – один з перспективних станів.

Дійсно, а не належить K(A) за визначенням. Якщо ж r ∈ Ф_a ∩ K(A), то r ∈ K(A) і тоді всі стани, які можна досягнути зі стану r, також належать K(A). За визначенням Ф_a стан а може бути досягнутий з r, але стан а не належить K(A), тобто отримали протиріччя.

Твердження 2. Якщо s і t – пара перспективних допустимих станів з виділеними дугами u_s = (s, x′/y, s₁) і u_t = (t, x′/y, t₁), і а=s або a=t, то для кожного вхідного слова р, яке не покриває із стану r ∈ Ф виділену дугу u_a, для стану b = φ(a) слово р не покриває виділену дугу u_b із стану φ(r)∈Ф, причому g(r, p)= g(φ(r), p).

Це твердження відразу випливає з визначення перспективної допустимої пари.

Позначимо через А(u_s,r_s,u_t,r_t) автомат, який є результатом перекиду в автоматі А двох дуг: дуги u_s=(s, x′/y, s₁) у стан r_s і дуги u_t=(t, x′/y, t₁) у стан r_t.

Теорема (про перекид двох дуг). Якщо s і t – пара перспективних допустимих станів з виділеними дугами u_s = (s, x′/y, s₁) і u_t = (t, x′/y, t₁), то автомат В = А(u_s, t₁, u_t, s₁) є ізоморфним заданому автомату А.

Доведення. Побудуємо відображення z: А→B наступним чином. Якщо стан а автомата А належить множині K(A), то покладемо z(a) = a, а якщо а належить множині Ф, то покладемо z(a) = φ(a).

З твердження 1 і означення φ випливає, що z є взаємно однозначним відображенням.

З визначення φ, твердження 2 і визначеного перекиду дуг випливає, що стани r ∈ Ф і φ(r) ∈ Ф еквівалентні. Дійсно, нехай g(r, p) = q. Можливі два випадки:

Слово р не покриває виділеної дуги u_a, де a=s або a=t. Тоді за твердженням 2 воно не покриває виділеної дуги u_b, де b = φ(a), і при цьому g(φ(a),p) = q;
Слово р покриває дугу u_a в автоматі А. Тоді р можна представити як p=p_ap′, де p_a не покриває виділеної дуги u_a, f(r, p_a) = a, а у слові p′ перший символ х′ покриває дугу u_a. За побудовою автомата В слово р покриває дугу u_b, де b = φ(a) в автоматі В. Згідно з відображенням φ p=p_bp′, p_b = p_a, f_b(φ(r), p_b) = b. З твердження 2 випливає, що g(r, p_a) = g(φ(r), p_b). Перекид дуги u_a виконано таким чином, що f(a,x′) = f_b(φ(a), x′). Зважаючи на те, що g(a,x′) = g_b(φ(a), x′), отримуємо, що g_b (r, p)=q.

Таким чином, стан r автомата А і стан φ(r) автомата В є еквівалентними. Теорему доведено.

Наведені достатні умови показують, що структура автоматів, які зберігають свою поведінку при двох перекидах дуг, є досить специфічною. Автору відомі приклади структур автоматів, поведінка яких витримує задану кількість перекидів дуг, і є припущення, що ці структури можна побудувати з елементарних структур, що відповідають розглянутому випадку двох перекидів.

Література

Мур Э.Ф. Умозрительные эксперименты с последовательностными машинами // Автоматы. – М.: Изд–во иностр. лит., 1956. – С. 179–210.
Козловский В.А. О классе графов, порожденных локальными преобразованиями заданного графа // Методы и системы технической диагностики. – Саратов: Изд–во Саратов. Ун–та. – 1985. – Вып.5. – С. 65–70.
Грунский И.С., Копытова О.М. О структуре контрольного эксперимента для определенно–диагностируемого автомата // Теория управляющих систем.– К.: Наук.думка, 1987. – С.40–54.
Грунский И.С., Козловский В.А., Пономаренко Г.Г. Представления конечных автоматов фрагментами поведения. – К.: Наук. Думка, 1990. – С. 232.
Капітонова Ю.В., Кривий С.Л., Летичевський О.А., Луцький Г.М. Печурін М.К. Основи дискретної математики. – К.: Наукова думка, 2002. – 568 с.