Необходимо рассчитать в трехмерном пространстве распространение выбросов в пространстве с течением времени.
Входные данные:
- направление ветра по розе ветров;
- давление воздуха;
- температура воздуха;
- данные для расчета концентрации (количество вредного вещества, выбрасываемого в атмосферу и т.д.);
- координаты выброса.
Выходные данные:
Величина концентрации во всех точках пространства в определенные моменты времени.
Концентрация по физическому смыслу является неотрицательной величиной, целесообразно использовать так называемые монотонные схемы, позволяющие получать неотрицательные решения. Воспользуемся методом расщепления по физическим процессам и на каждом малом интервале времени [tj, tj+1] длиной Δt [1].
Перенос примеси по траекториям:

где wg описывает гравитационное оседание субстанций, u, v и w – скорости ветра по осям x, y, z соответственно. φ – искомая концентрация.
Этот этап является одним из основных в процессе переноса[2].
Для простоты изложения рассмотрим основной элемент схемы на примере одномерного уравнения:
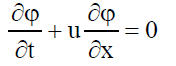
Схема Куранта - Изаксона - Риса. Обобщение схем КИР на квазилинейный случай (при использовании дивергентной формы записи уравнений) очевидно:
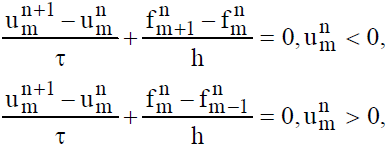
где u – искомая функция концентрации, ƒ – функция описывающая источник дыма (его мощность выброса и т.д.), τ – шаг по времени, h – шаг в пространстве.

Рисунок 1 — Распространение выброса
Схема устойчива при выполнении условия Куранта:
 (если условие не выполняется то решение может не сойтись)
(если условие не выполняется то решение может не сойтись)
Вследствие перегретости, примесь в начальной фазе своего распространения обладает восходящей скоростью, но эта начальная фаза непродолжительна, т. к. под действием турбулентности температуры частиц примеси и воздушной среды быстро выравниваются. Точно учесть указанный эффект чрезвычайно трудно, так как пришлось бы решать совместно уравнения диффузии и свободной конвекции частиц газа. Однако даже при значительных перегревах газа этот эффект можно учесть приближенно, заменяя реальный источник примеси геометрической высоты H фиктивным, несколько приподнятым источником, высота которого ΔH.
Существует большое количество полуэмпирических и эмпирических формул, предложенных разными авторами для определения ΔH. По проведенным оценкам (Бем, 1971) наиболее приемлемо ?H определяется для нейтральной стратификации атмосферы по формулам Пристли, Спэра, Берлянда, Дановича–Зайгеля. В связи со сказанным для определения начального подъема ΔH газовой струи была выбрана следующая полуэмпирическая формула (Берлянд, 1975):

где Tв, Ta – соответственно температуры выбросов газа и окружающего воздуха по абсолютной шкале, w – начальная скорость выброса газов, R – радиус устья трубы, g – ускорение свободного падения, u – скорость ветра на высоте флюгера.
Рассчитываем ΔH, это фактически расстояние на котором газ остынет и начнёт опускаться. Значит вокруг трубы можно выделить сферу радиуса ΔH с вертикальными скоростями направленными вверх причём в центре сферы скорость подъёма равна начальной скорости газа, а на границах нулю.
Учёт ландшафта создаётся вследствие введения такой системы координат:

где H – верхняя граница расчёта, ƒ(x,y) – функция высот ландшафта.
В такой системе координат ландшафт должен быть гладким, производная должна быть монотонной, иначе в местах перепадов не будет выполняться условие Куранта и решение может расходиться. А на гладких ландшафтах учёт ландшафта не заметен.
Проанализируем алгоритм для применения на распределенных системах.
Выполнять пока выполняется условие Куранта или загрязнение не достигло какой-либо точки:
1. Инициализация матрицы концентраций в пространстве φ[,,,]
2. Расчет новой матрицы концентраций φ’[,,,] для следующего момента времени t+Δt
3. Визуализация результата.
4. Присвоение φ[,,,]=φ’[,,,].
При моделирование обсчитывается трехмерная матрица, которую можно разбить на подматрицы, которые могут обсчитываться независимо, однако могут возникнуть проблемы в пограничных точках.
В данном случае предыдущая схема распределения вычислений использовать нерационально, так как через каждый шаг времени необходима синхронизация данных между потоками. В данном случае, учитывая закон Амдала, более рационально использовать вычислительные ресурсы для более точной проработки сценариев развития (изменение во времени таких параметров как скорость и направление ветра и т.д.) [3].
Рисунок 2 — Условная схема распределения вычислений по потокам

Рисунок 3 — Архитектура системы
Таким образом, использование распределенных систем при решении исследуемой задачи может уменьшить время решения задачи при определенных условиях. Также, в виду использования распределенных ресурсов становится возможным более эффективное использование вычислительных ресурсов. Выбор технологии реализации решения данной задачи зависит от особенностей вычислительных ресурсов на предприятии.
1. В.А. Алексеев, А.В. Арефьев. Адаптивный экологический мониторинг окружающей среды // Экология и промышленность России. 2003. № 10. С. 11-13.
2. Алоян А.Е. Динамика и кинетика газовых примесей и аэрозолей в атмосфере. М.: ИВМ РАН, 2002. 201 с.
3. Корнеев В.Д. Параллельное программирование в MPI. Новосибирск: Изд-во СО РАН, 2000. 213 с.