О.В. Ложкина, кандидат химических наук, доцент;
В.В. Попов, кандидат военных наук.
Санкт-Петербургский университет ГПС МЧС России.
А.Д. Кузнецова.
Санкт-Петербургский университет сервиса и экономики
Приводится критический анализ применимости физико-математических моделей атмосферной диффузии для исследования загрязнения атмосферного воздуха вредными выбросами автомобильного транспорта. Рассматриваются специфические характеристики состава отработавших газов, закономерности их миграции и метаболизма в стратифицированной атмосфере. Демонстрируются карты мониторинга загрязнения атмосферы на примере кольцевой автомагистрали Санкт-Петербурга.
Ключевые слова: математическая модель, атмосферная диффузия, автомобильный транспорт, загрязнение воздуха
ANALYSIS OF THE PHYSIC-MATHEMATICAL MODELS OF THE ATMOSPHERIC DIFFUSION FOR ESTIMATION OF THE INFLUENCE OF THE CARS ON TOWN AMBIENCE
O.V. Lozhkina; V.V. Popov.
Saint-Petersburg university of State fire service of EMERCOM of Russia.
A.D. Kyznecova. Saint-Petersburg state university of service and economics
Kritical analysis of applicability of the physic-mathematical models of the atmospheric diffusion happens to in artifor study of the soiling the air bad surge cars; cards of the monitoring the contamincle ation of atmosphere are demonstrated on example of the recirculating superhighway Saint-Petersburg.
Key words: mathematical models, atmospheric diffusion, motor transport, soiling the air .
Первой задачей, которую приходится решать при построении теории прогнозирования негативного воздействия автотранспорта на качество воздушной среды города, является выбор методики оценки распространения загрязняющих примесей в воздушной среде.
Для получения достоверных характеристик об уровне загрязнения атмосферы вредными выбросами автотранспорта необходимо проводить многочисленные и достаточно широкомасштабные отборы проб с установлением концентраций газов и аэрозольных выпадений вблизи автомагистралей на протяжении нескольких лет, что очень дорого [1, 2].
Поэтому данная проблема на практике решается построением физико-аналитических (математических) моделей процессов эмиссии и рассеивания вредных веществ в атмосфере с допущениями, адекватными точности конкретно решаемых практических задач [3–5].
Если расчетные оценки по выбранной (обоснованной) модели совпадут (с определенной точностью) с результатами измерений, то количество измерений можно существенно сократить, а для стилизованных схем, например, условно точечных или площадных источников выбросов, и вовсе избежать [1, 6].
При моделировании процесса переноса веществ в атмосфере рассматриваются три основных аспекта [1–5]:
Авторами анализируются возможности использования современных подходов моделирования переноса и рассеивания загрязнителя в атмосфере, применяемых в РФ и за рубежом, для решения задач, связанных с загрязнением атмосферы автомобильным транспортом.
Методы исследования метеорологического режима и загрязнения атмосферы городов подразделяют на [7]:
Эмпирико-статистические и статистические методы связывают между собой различные метеорологические параметры и свойства «подстилающей» поверхности. К статистическим относят регрессионные и авторегрессионные модели. Статистические модели подробно описываются в [4, 5] и используются, например, для расчета среднего загрязнения атмосферы. Для вывода уравнения регрессии, как правило, применяется формула Гаусса («Гауссовы модели»).
Математические модели в [7] делятся на две категории: энергетические и гидродинамические модели.
Энергетические модели (в [7] такие модели называются также статическими) предназначены для изучения метеорологического режима в приземном слое воздуха над городом. Основой метода является уравнение теплового баланса.
Метод гидродинамического моделирования в [7] характеризуется как наиболее плодотворный и перспективный. Он основывается на решении системы уравнений, описывающих метеорологический режим формирования воздушного потока в городской среде в зависимости от горизонтальной и вертикальной составляющих скорости ветра, температуры, удельной влажности, горизонтального и вертикального градиентов давления, силы Кориолиса и других физических параметров.
В целом по анализу работ [1–7] можно выделить четыре основных направления, в которых развивалось моделирование распространения газообразных примесей и твердых частиц в атмосфере городов.
1. Использование статистических моделей распространения, основанных на функции распределения Гаусса. Данное направление заключается в использовании моделей распространения, предназначенных для ровной подстилающей поверхности, модифицированных путём введения эмпирических коэффициентов, учитывающих возможное перераспределение концентрации в застойных зонах вблизи зданий и сооружений.
2. Моделирование течений в уличных каньонах на основе решения транспортно-диффузионных уравнений.
3. Физическое моделирование в аэродинамических трубах. Подобные эксперименты дают возможность оценить некоторые особенности распределения примеси в условиях застройки для таких метеорологических условий, которые можно с той или иной точностью воспроизвести в аэродинамической трубе. При этом в трубах невозможно соблюсти подобие течения по достаточному набору критериев, например, числа Рейнольдса одновременно с числом Росби. В то же время такой метод позволяет определить некоторые необходимые для моделирования параметры и дает возможность сравнения расчетов по модели с измерениями, например, – оценить распределение воздушных потоков вдоль улиц при различных направлениях ветра.
4. Построение моделей на основе комплексного подхода: сравнительного анализа результатов натурных экспериментов, результатов численного моделирования и физического моделирования. При этом проводится анализ результатов натурных экспериментов с результатами численного и физического моделирования с последующим построением параметрических моделей распределения примеси в уличных каньонах в зависимости от метеоусловий: скорости и направления ветра, температурной стратификации атмосферы, влажности и т.п.
Теоретические исследования крупномасштабных движений в атмосфере внутри, так называемых, конвективных колонок основываются на фундаментальных представлениях об аэродинамике воздушной среды.
Первые теоретические исследования о свободно-восходящих струях над точечными источниками тепла были теоретически рассмотрены Я.Б. Зельдовичем для ламинарных и турбулентных струй [1].
В ряде работ для количественного описания динамики развития конвективных течений в атмосфере [1] используются как аналитические зависимости теории свободно конвективных струй, так и не одномерные математические модели, которые реализуются численными методами, например, с помощью уравнений несжимаемой среды в приближении Буссинеска.
Модели, основанные на уравнениях Навье-Стокса [1] для вязкого, сжимаемого и теплопроводного газа, учитывают диффузию аэрозольных частиц и влияние фазовых переходов, обусловленных наличием влаги в атмосфере, динамику подъема и зависания конвективной колонки.
Метод Навье-Стокса предполагает численное решение уравнений турбулентной диффузии. Важным достоинством этих моделей является то, что уравнение турбулентной диффузии естественным образом увязывается с физическими процессами, протекающими в атмосфере. Они позволяют прогнозировать пространственно-временную картину загрязнения атмосферы, но только при нормальных метеорологических условиях, что не всегда наблюдается и не дает возможности рассмотреть экстремальные, по гидрометеорологии, воздействия АТС на городскую среду.
Для моделирования процессов загрязнения воздуха и построения полей концентраций на малых и средних расстояниях от источника выбросов (что наиболее близко отражает физическую картину загрязнения атмосферы автомобильными выбросами) существует два подхода – на основе рассеивания по формулам Гаусса, который предполагает оценку распределения концентраций загрязнителей вдоль координатных осей и на основе теории массопереноса (так называемые, «градиентные» модели или К-модели, основанные на решении уравнений турбулентной диффузии [6, 8, 9].
За рубежом широко используются различные версии гауссовых моделей [4, 5, 7]. К таким моделям относятся – американские модели HIWAY-2, CALINE-4 (California Line Source Model), GM (General Motors), GFLSM (General Finite Line Source Model), финская модель – CAR-FMI (Contaninants in the Air from a road, By the Finnish Meteorological Institute). В моделях HIWAY-2 и CALINE-4 концентрации рассчитываются для конечного линейного источника при произвольном направлении ветра; в процессе расчетов источник делится на серию элементов, от которых рассчитываются концентрации, которые затем суммируются. Модель GFLSM основывается на формулах для бесконечного линейного источника.
Основу моделирования распространения загрязнителей на основе статистического описания процессов турбулентности положили работы Сеттона, Пасквилла, Гиффорда [1, 7]. Модели строятся на предположении, что шлейф загрязняющего вещества имеет гауссово распределение и концентрация в заданной точке по направлению ветра может быть рассчитана с помощью обобщенного уравнения Гаусса. Такие модели нашли широкое применение благодаря простоте и получению результатов, согласующихся с экспериментом. Гауссовы модели официально рекомендованы Европейской экономической комиссией, метеослужбами ряда стран [7].
Основная модель для случая постоянной скорости ветра и отсутствия химической трансформации представляется формулой:
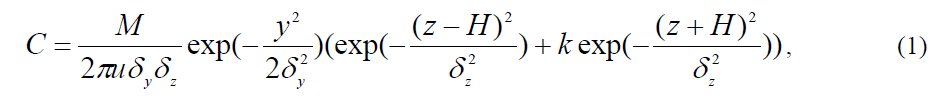
где: С – концентрация загрязняющего вещества, г/м3; М – мощность выброса, г/с; u – скорость ветра на высоте Н, м/с; δy, δz – параметры горизонтальной и вертикальной дисперсии, м; y – расстояние от средней линии шлейфа, м; z – высота над землей, м; k – коэффициент отражения ( 0 ≤ k ≤ 1); H – конечная высота подъема шлейфа, м.
Уравнение (1) действительно для концентраций, усредненных во времени для нескольких минут, то есть для интервала времени, для которого представительными являются значения параметров рассеивания и скорости ветра. Достоинства модели, благодаря которым она нашла наибольшее применение при расчетах загрязнения атмосферы в большинстве стран мира, заключается в следующем.
1. Поле концентрации от одного или нескольких источников выбросов описывается алгебраическими соотношениями, благодаря чему машинные реализации этой модели отличаются высоким быстродействием и не требуют больших объемов памяти.
2. Гауссово приближение рассеяния позволяет учитывать множество факторов, влияющих на уровни концентраций примесей в приземной атмосфере. В числе этих факторов выделяют – метеоусловия (скорости ветра и устойчивости атмосферы), отражение примеси от подстилающей поверхности и приподнятые инверсии, выведение примеси из атмосферы осадками, вследствие сухого осаждения и химической трансформации. Модель позволяет учитывать характер поверхности, над которой распространяются загрязняющие воздух вещества: степень застройки, влияние леса или открытой поверхности.
3. Результаты расчетов по модели и многочисленные экспериментальные наблюдения, выполненные исследовательскими коллективами, в том числе ГГО им А.И. Воейкова [1–7], показали хорошее соответствие между собой: погрешности расчетов по модели оцениваются в несколько десятков процентов. В некоторых случаях различия могут достигать 2–3 раз. Оценки загрязнения атмосферы в пределах этих погрешностей удовлетворяют большинству практических задач.
Основные причины, приводящие к различиям при сравнении измеренных и рассчитанных концентраций, связаны с неточностью определения величины выбросов загрязняющих веществ из источников загрязнения, неопределенностью в выборе категории устойчивости атмосферы, погрешностями измерений метеопараметров.
Основным недостатком гауссовой модели является то, что она рассматривает начальное состояние атмосферы как невозмущенное, а распределение температуры, давления, инверсии, влажности воздуха и других физических параметров по высоте сводит к соответствию с моделью Международной стандартной атмосферы, что в реальных условиях никогда не наблюдается. Как известно из многочисленных исследований, метеорологические условия являются одним из самых важных факторов, влияющих на рассеивание и распределение концентраций вредных веществ в атмосфере. Модель позволяет спрогнозировать пространственно-временную картину загрязнения атмосферы, не учитывая (не привязываясь) конкретно к рельефу местности и метеорологическим условиям территории.
Гауссов подход, по сути, является сугубо эмпирическим, что препятствует обобщению его результатов в целом ряде практически важных случаев. Он не учитывает зависимость диффузионных коэффициентов от высоты источника, поэтому позволяет описывать приземное поле концентраций примеси от источника только фиксированной высоты [7].
Модели на основе К-теории базируются на уравнениях турбулентной диффузии и являются наиболее проработанными в теоретическом плане. Россия занимает лидирующее место в мире по этим моделям. В России большее распространение получила модель М.Е. Берлянда [1, 5, 9].
В соответствии с данным подходом степень загрязнения воздуха выбросами вредных веществ из непрерывно действующих источников определяется по наибольшему рассчитанному значению разовой приземной концентрации (См), которая устанавливается на некотором расстоянии (Хм) от места выброса при неблагоприятных метеорологических условиях, когда скорость ветра достигает опасного значения (Uм) и в приземном слое происходит интенсивный турбулентный обмен. Алгоритм и порядок проведения расчетов полей максимальных концентраций изложены в «Методике расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. ОНД-86» [3].
Согласно с данным методом процесс переноса вредных веществ описывается уравнениями турбулентной диффузии в атмосфере. Применяя затем приемы усреднения переходят от уравнения диффузии для мгновенных концентраций к уравнению турбулентной диффузии для средних значений концентраций.
Подход М.Е. Берлянда применим только при условии, что размерность облака выброса больше, чем размер доминантной турбулентности. Вообще, все модели, построенные на решении уравнения турбулентной диффузии наиболее применимы к описанию вертикальной диффузии у поверхности земли на расстояние, не более 10 км от источника, что приемлемо для автомагистралей.
Модели на основе уравнений турбулентной диффузии позволяют на единой основе решить множество практических задач и при этом: учесть застройку, рельеф местности, время осреднения (разовые, годовые), фотохимические реакции, метеоусловия (нормально неблагоприятные и аномально неблагоприятные). Также возможно рассмотрение различных видов источников: точечного, линейного, площадного.
Можно сделать вывод, что процесс переноса по модели М.Е. Берлянда применим для недостаточно мощных источников, так как она не рассчитана на сильный перегрев газов в зоне источника и наличие мощного турбулентного перемешивания в результате перегрева. Следовательно, модель можно использовать для описания переноса относительно холодных, стационарных во времени выбросов, какими можно считать выбросы от потока АТС.
Теоретические закономерности распространения и пространственно-временного распределения загрязняющих примесей в атмосфере определяются путем решения уравнения атмосферной диффузии. Это уравнение (2) в частных производных, по сути, представляет собой математическую формализацию фундаментального физического закона сохранения потока вещества и в этом смысле дает универсальное описание закономерностей распространения атмосферных примесей.
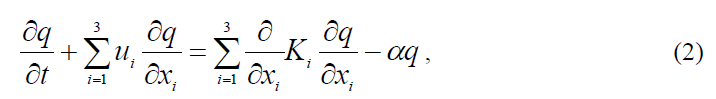
где: q – рассчитываемая примесь; xi – координаты примеси, в дальнейшем обозначаются через х, у, z; ui; Ki – составляющие средней скорости перемещения примеси и коэффициента обмена, относящиеся к направлениям оси xi (i = 1, 2, 3); α – коэффициент, определяющий изменение концентрации за счёт атмосферного метаболизма (превращения примеси).
Использование данного фундаментального подхода математического моделирования турбулентной диффузии, который часто называют К-теорией [7], совместно с обоснованными упрощениями и эмпирическими уточнениями, лежащими в основе нормативного документа по расчету рассеивания вредных веществ в атмосферном воздухе «ОНД-86» [3], нашло выражение в математической модели (3) для холодных выбросов. По данному выражению рассчитываются значения наибольшей суммарной концентрации вредной примеси См (мг/м3), которая устанавливается на некотором расстоянии (Хм) от места выброса от транспортных средств как от близко расположенных друг к другу источников на отдельных участках магистралей.

где А – коэффициент, зависящий от температурной стратификации атмосферы; М – масса вредного вещества, выбрасываемого в атмосферу в единицу времени (г/с), в случае автотранспортного потока – масса вещества, выбрасываемого группой автомобилей, образующих поток; F – безразмерный коэффициент, учитывающий скорость гравитационного оседания твердых частиц (пыли) в атмосферном воздухе на подстилающую поверхность, при расчете рассеивания в атмосфере сажи при работе двигателей передвижных транспортных средств рекомендуется принимать значения параметра F = 1; m' – безразмерный коэффициент, равный 0,9; η – безразмерный коэффициент, учитывающий влияние рельефа местности, в случае ровной или слабопересеченной местности с перепадом высот, не превышающим 50 м на 1 км, η = 1; Н – высота магистрали, как неорганизованного источника выброса, над уровнем земли.
Таким образом, транспортные потоки произвольных геометрической конфигурации и распределения интенсивности движения транспортных средств по автомагистралям и улицам представляются в виде совокупности точечных, линейных и площадных источников вредных выбросов, путем суммации которых определяется общее загрязнение воздушной городской среды.
Использование такой расчетной схемы позволяет учитывать целый ряд важнейших для оценки воздействия автотранспорта факторов:
Очевидно, что для получения достоверных результатов расчетного мониторинга загрязнения атмосферного воздуха требуется реальная, то есть весьма специфичная (по условиям применения автотранспорта) и, одновременно, полная (по структуре транспортных средств) информация о мощности выбросов и ее распределения по территории города, причем, в наиболее опасные по времени суток, так называемые, часы пик. Эта задача решается путем непосредственного инструментального наблюдения за интенсивностями движения и структурными распределениями транспортных средств по характерным группам и экологическим классам. При этом выбросы предлагается определять с учетом требований Технического регламента Постановления Правительства РФ № 609 от 12 октября 2005 г. [11].
На рисунке представлен фрагмент выполненных в 2011 г. экспериментально-расчетных исследований загрязнения атмосферы вблизи кольцевой автомагистрали Санкт-Петербурга (карта загрязнения воздуха NO2).
Правильность выбора основополагающей математической модели для оценки загрязнения воздуха выбросами автотранспорта подтверждают положительные результаты ранее проведенных экспериментальных исследований других авторов [9], а также сопоставления результатов расчетов с данными инструментального мониторинга воздушной среды автоматическими станциями измерения загрязнения воздуха (АСИЗВ) в Санкт-Петербурге при соответствующих метеоусловиях [10].
Применение численных методов расчета воздействия автотранспорта на городскую среду с использованием данных непосредственных наблюдений интенсивностей и структуры потоков на автомагистралях, позволит более взвешенно принимать управленческие решения и неотложные меры по улучшению экологической ситуации городов.

Рисунок 1 — Карта загрязнения воздуха NO2
1. Берлянд М.Е. Современные проблемы атмосферной диффузии и загрязнения атмосферы. Л.: Гидрометеоиздат, 1975. 448 с.
2. Ложкин В.Н., Медейко В.В. Модели оценки экологического ущерба, применяемые в Российской Федерации, США и странах ЕС, при государственном регулировании воздействия транспортных средств на окружающую среду // Информационный бюллетень. № 2 (32). «Вопросы охраны атмосферы от загрязнения». СПб.: НПК «Атмосфера» при ГГО им. А.И. Воейкова, 2005. С. 103–116.
3. Общесоюзный нормативный документ Госкомгидромета СССР (ОНД-86). Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. Л.: Гидрометеоиздат, 1987. 93 с.
4. Kukkonen J., Harkonen J., Walden J. Evaluation of the dispersion model CAR-FMI against data from a measurement campaign near a major road. Atmospheric Environment, 2001. Vol. 35/5. Р. 949–960.
5. Uliasz M., Stocker R.A., Pielke R.A. Regional modelling of air pollution transport in the south-western USA. (In:) Zannetti P. (ed.), Environmental Modelling Vol. III Comput. Mech. Public. Southampton, 1996.
6. Буренин Н.С., Оникул Р.И., Соломатина И.И. К оценке выбросов автотранспорта в атмосферу и загрязнения воздуха вблизи автомагистралей: тр. ГГО. Вып. 436. 1797. С. 102–110.
7. The wind field model. [Электронный ресурс]. URL: http://www.indic-airviro (дата обращения: 22.02.2012).
8. Ложкин В.Н., Артамонов В.С., Баскин Ю.Г. К вопросу управления риском биоэкологического воздействия автомобильного транспорта на население крупного города // Вестник Санкт-Петербургского университета МВД. 2000. № 4(8). С. 110–116.
9. Berlyand M.E., Burenin N.S., Genihovich E.L. Experimental investigation of atmospheric pollution due to motor vehicles. Proc. Sov. American. Symp on mobile sourses of air pollution. V. l. Saint-Petersburg. 1992. Р. 105–121.
10. Сорокин Н.Д. Система мониторинга атмосферного воздуха в Санкт-Петербурге: доклад IV Междунар. науч.-практ. конф. «Автотранспорт: от экологической политики до повседневной практики»: VIII Междунар. экологический форум 20–21 марта 2008 г., Санкт-Петербург.