Работа посвящена вопросам определения характера загрязнения приземного слоя атмосферы от промышленных источников. В работе построена математическая модель для описания нестационарной трехмерной динамики загрязнений, в том числе от нестационарных источников для конкретного задаваемого физического состояния атмосферы. В предлагаемом подходе используется прямое численное интегрирование точных уравнений переноса примеси в атмосфере с учетом основных физических факторов, что приближает данный метод к проведению вычислительного эксперимента. На основе разработанной математической модели создана информационная система для компьютерного моделирования процесса распространения при месей от промышленных источников, расположенных на территории предприятия.
Расчеты динамики переноса примесей в атмосфере позволяют ответить на многие вопросы экологии промышленных зон. Получение карт загрязнений посредством расчета на ЭВМ особенно актуально применительно к веществам, для которых лабораторные измерения концентрации сопряжены с большими затратами, а также для примесей, не выбрасываемых непосредственно в атмосферу, но возникающих в ней в результате химических превращений обычных загрязнителей. С помощью компьютерных программ, основанных на прямом решении на ЭВМ математических уравнений, описывающих исследуемый процесс, строятся информационно-математические модели промышленных районов. Такие модели позволяют осуществлять экологический мониторинг за состоянием воздушно-водного бассейна, включая последствия различного рода аварий, газовок и т. п., примеры которых многочисленны.
Отличительной чертой математического моделирования, основанного на численном интегрировании нестационарных уравнений переноса, в отличие от официальных методик типа ОНД-86 (ОНД), является принципиальная возможность учета любых влияющих внешних факторов (метеоусловия, ветер, рельеф местности, солнечная радиация, химические и фотохимические превращения и т. п.) на «математическом уровне», то есть путем введения требуемых факторов в систему математических уравнений. Заметим, что для построения карт загрязнения в рамках рассматриваемой модели не требуются многолетние наблюдения параметров состояния атмосферы и распределения массы загрязняющих веществ по источникам выбросов. Достаточно данных на текущий момент. Это позволяет учитывать последствия нестационарных процессов – аварии, газовки, изменение метеоусловий со временем и т. п. Проблема оценки уровня загрязнения нижних слоев атмосферы и подстилающей поверхности является одной из центральных в экологии промышленных районов. Теоретические исследования, основанные, как правило, на численном решении модельных уравнений и статистическом анализе, позволяют во многих случаях дать приемлемые прогнозы распределения концентраций примесей (см.: [3; 8; 17; 19].
Компьютерная модель предназначена для получения оперативной информации, необходимой для улучшения экологической обстановки в регионе. Ее можно использовать в качестве одного из инструментов, позволяющих проводить контроль предприятию за загрязнением окружающей среды. Система может служить основой при проведении природопользовательских и экологических экспертиз при размещении различных производств. Возможно определение метеорологических условий, при которых загрязнение приземного слоя атмосферы максимально и минимально.
Математическая модель основана на численном интегрировании системы нестационарных уравнений в частных производных с источниками, которая описывает процесс переноса загрязняющих примесей с учетом основных физических факторов. Основными компонентами компьютерной системы являются:
1) Модель приземного слоя атмосферы.
Модель приземного слоя атмосферы учитывает метеорологические и климатические условия (направление и силу ветра, температуру воздуха, конвективное состояние атмосферы). Скорость ветра и амплитуда турбулентных пульсаций задается в м/с. Направление ветра задается в градусах от западного направления, либо выбирая из 16 определенных направлений. Конвективное состояние приземного слоя определяется в первую очередь вертикальным градиентом температуры.
2) Модель динамики загрязняющих примесей.
Расчет динамики распространения примесей учитывает основные физические факторы, определяющие этот процесс: ветровой снос, диффузионный перенос, осаждение на поверхность земли и повторное загрязнение. Значения коэффициентов турбулентной диффузии задаются на основе стандартной модели ОНД-86 (ОНД).
На процесс распространения примесей в атмосфере оказывают влияние множество факторов, но основными являются два: ветровой снос и диффузионное расплывание. Эти два физических эффекта можно учесть в рамках математической модели, в основе которой лежит дифференциальное уравнение в частных производных:
Источники загрязнения устанавливаются функцией Q, которая определяет временную динамику выбросов, их параметры (координаты и мощность выбросов, высоту труб, температуру; для плоскостных источников задается пространственное распределение загрязнителей). Уравнение (1) записано в векторной форме. Для решения задачи распространения примеси в приземном слое атмосферы удобно работать в декартовой системе координат: x и y – координаты в плоскости поверхности земли, а z – вертикальная координата. Слагаемое ∂ρ ⁄ ∂t описывает изменение концентрации примесей со временем в точке с координатами (x, y, z).
Риcунок 1 — Схема, поясняющая принцип и структуру работы созданного программного комплекса.
Стрелками указаны направления потока данных
Запишем уравнение (1) в декартовой системе координат:
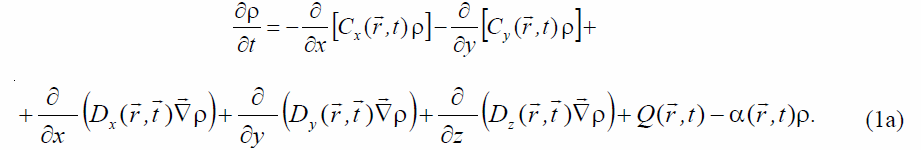
Величины Dx, Dy, Dz, Cx, Cy являются эмпирическими параметрами, учитывающими как состояние атмосферы, так и рельеф местности. Характер функциональной зависимости коэффициента диффузии и скорости ветра в работах различных авторов принимается приблизительно одинаковым. Можно считать, что коэффициент диффузии D на небольших высотах линейным образом зависит от величины скорости ветра, не обращаясь, однако, в нуль при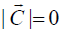 
. Поэтому в нашей модели принято
В зоне перемешивания для коэффициента диффузии имеем:
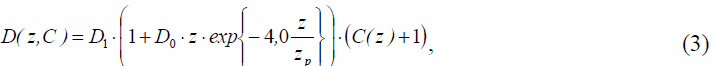
где значения параметров D0, Zp сказываются только на высотах z < (2-3) zp ( zp - высота пограничного слоя). В зависимости от стратификации атмосферы высота эффективного перемешивания в вертикальном направлении может сильно меняться в пределах от 50 до 1 000 м.
Первое слагаемое справа в формуле (1) обусловлено ветром в плоскости земли 
:
где необходимо учитывать наряду с постоянной составляющей .png)
и флуктуирующую часть .png)
. Среднее направление ветра в каждой точке плоскости (x, y) характеризуется углом φ0 width=2%> между осью x и направлением ветра, а дисперсия направлений задается параметром σφ. Тогда при нормальном распределении направлений ветра
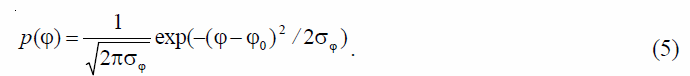
Зависимость скорости ветра от вертикальной координаты для базовой модели выбираем в виде:
где величина Cg – характеризует скорость ветра у поверхности Земли; параметр z0 – определяет шероховатость поверхности. В общем случае можно задавать произвольное распределение C(z).
К исходным данным для проведения расчетов по этой методике необходимо знание источников загрязнения – координаты, высота, химический состав и объем выбросов, включая пространственно распределенные источники – пруды-накопители, дороги, карьеры. Информация по источникам соответствует принятой в общероссийской методике ОНД-86.
Характер источников может быть произвольный, определяется целями расчета, в частности, различают стационарные и нестационарные, точечные, плоскостные и объемные источники. Основными источниками для модели горения прудов-накопителей являются плоскостные источники, а при моделировании динамики выбросов от промышленных предприятий – точечные источники.
Высота выброса примеси в атмосферу, дальнейшее ее рассеяние и осаждение зависят не только от высоты источника (трубы), но и от таких параметров примеси, как температура и скорость ее вытекания из трубы. Пусть труба имеет высоту H0, ее радиус на выходе примеси – R0, скорость выноса из жерла трубы – ω0, температура атмосферы – Ta и температура примеси – Ta + ΔT. Тогда эффективная добавка ΔH к высоте трубы H0 (H = H0 + ΔH) удовлетворительно аппроксимируется соотношением:
Здесь первый член описывает вертикальную инерцию примеси, а второй – ее дополнительную «архимедову» плавучесть.
В зависимости от величины и знака вертикального градиента температуры, исходящая из локализованных и распределенных источников примесь может либо «всплыть» в верхние слои атмосферы (турбулентная конвекция), либо прижиматься к земле и накапливаться в приземном слое толщиной порядка высоты деревьев и зданий. И в первом, и во втором случае соответствующие эффекты можно описать с помощью модельного параметра α. Однако второй из указанных факторов, как наиболее опасный в экологическом отношении, необходимо учесть с помощью локального уравнения «накопления»:
Как известно, абсолютное значение вертикального градиента температуры и его знак характеризует температурную стратификацию, которая является важным фактором, способствующим увеличению или уменьшению концентрации вредных примесей. Влияние температурной устойчивости атмосферы на турбулентный обмен оценивается по безразмерной величине β, аналогичной по физическому смыслу числу Ричардсона Ri. Последняя величина характеризует отношение разности температур на выбранных уровнях к скорости ветра 
. Можно говорить, что атмосфера стратифицированно неустойчива при β ≥ 0,06, устойчива при β ≤ 0,05 и нейтральна при β ≈ 0.
Общая структура информационной системы показана на рисунке 1.
Важным компонентом модели является электронная карта. Вся моделируемая область покрывается сеткой размером N × M × K. В вертикальном z-направлении в простейшем случае достаточно ввести несколько слоев (K ≥ 5), которые учитывают перенос примесей в вертикальном направлении и взаимообмен между приземным слоем атмосферы, верхними слоями и подстилающей поверхностью в соответствии с вышеизложенным. С построенной моделью проводились несколько серий тестирований. Во-первых, исследовалась роль внутренних параметров модели (выбор сетки, временной шаг интегрирования, граничные условия). Во-вторых, варьировались физические условия моделирования (ветровой и диффузионный режимы, стратификация атмосферы, режим вымывания примесей из атмосферы). Наконец, рассмотрены различные режимы работы загрязняющих источников (см. рис. 2 и 3).
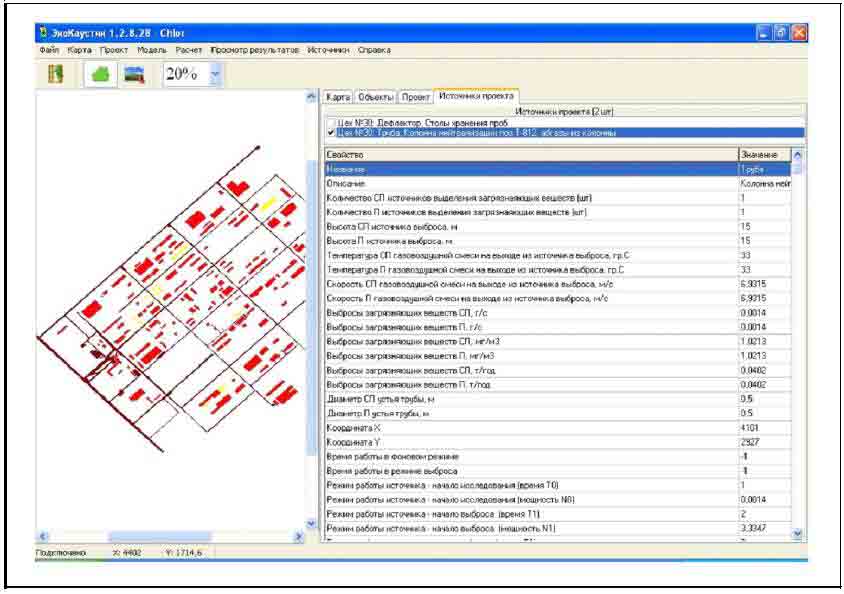
Рисунок 2 — Вид главного окна программы «ЭкоПром»
с открытым окном «Источники проекта»
Рисунок 3 — Вид главного окна программы «ЭкоПром» во время проведения расчетов
Опишем алгоритм построения численного решения уравнения адвекции – диффузии на примере одномерного уравнения вида:
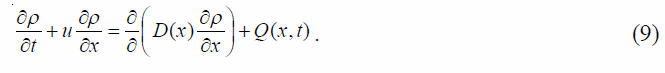
Явная конечно-объемная схема для уравнения (1) имеет вид:
где индекс i обозначает номер ячейки; n – номер временного слоя; индексами i ± 1/2 обозначены величины, относящиеся к границам ячеек; ƒ = u × ρ – поток.
Схема (10) устойчива при ограничении на шаг интегрирования согласно условию:
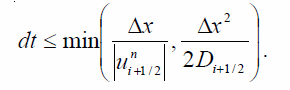
Для подавления осцилляций, возникающих при численной аппроксимации адвективных слагаемых (второе слагаемое в 1 или 2), потоки через границы ячеек аппроксимируются TVD-схемой
В тестовых расчетах были использованы различные варианты ограничителей, мы остановили свой выбор на ограничителе ван Лира 
, представляющем хороший компромисс между численной диффузией решения и затратами на его вычисление. Расчеты, проведенные по схеме (10), показали полное отсутствие осцилляций численного решения даже при больших числах Пекле, когда адвекция доминирует над диффузией.
Основными компонентами данной информационной системы являются:
1. Основная графическая оболочка управления информационной системы.
2. Расчетный модуль для численного моделирования нестационарной трехмерной динамики примеси.
3. Картографический блок территории предприятия, включая санитарно-защитную зону предприятия.
4. Электронную базу данных источников промышленных выбросов.
5. Электронную базу данных входных параметров для расчетного модуля, который включает подсистему метеорологических и физических параметров.
6. Модуль визуализации динамики примеси непосредственно во время проведения моделирования.
7. Графический блок для визуализации проведенных расчетов.
8. Блок для генерации отчетов.
1. Белов, И. В. Транспортная модель распространения газообразных примесей в атмосфере города / И. В. Белов, М. С. Беспалов, Л. В. Клочкова [и др.] // Математическое моделирование. – 2000. – Т. 12, № 11. – С. 38–46.
2. Белослудцев, А. А. Информационная система для создания электронных карт с рельефом (GeoMapBuilder) / А. А. Белослудцев, Н. В. Наводченко, А. В. Хоперсков // Свидетельство об официальной регистрации программ для ЭВМ № 2007612682 от 21.06 2007 г.
3. Берлянд, М. Е. Прогноз и регулирование загрязнения атмосферы / М. Е. Берлянд. – Л. : Гидрометеоиздат, 1985. – 272 с.
4. Берлянд, М. Е. Современные проблемы атмосферной диффузии и загрязнения атмосферы / М. Е. Берлянд. – Л. : Гидрометеоиздат, 1975. – 418 с.
5. Гуди, Р. М. Атмосферы : пер. с англ. / Р. М. Гуди, Дж. Уолкер. – М., 1975.
6. Замай, С. С. Модели оценки и прогноза загрязнения атмосферы промышленными выбросами в информационно-аналитической системе природоохранных служб крупного города / С. С. Замай, О. Э. Якубайлик. – Красноярск : Изд-во Краснояр. гос. ун-та, 1998. – 109 с.
7. Крукиер, Л. А. Математическое моделирование процессов переноса в несжимаемых средах с преобладающей конвекцией / Л. А. Крукиер // Математическое моделирование. – 1997. – Т. 9, № 2. – С. 4–12.
8. Марчук, Г. И. Математическое моделирование в проблеме окружающей среды / Г. И. Марчук. – М. :Наука, 1982. – 320 с.
9. Матвеев, Л. Т. Основы общей метеорологии. Физика атмосферы / Л. Т. Матвеев. – СПб. : Гидрометеоиздат, 2000. – 751 с.
10. Методика оценки последствий аварийных выбросов опасных веществ (Методика «Токси». Редакция 3.1). – М., 2005.
11. Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. Общесоюзный нормативный документ (ОНД-86) / Госкомгидромет. – Л. : Гидрометеоиздат, 1987. – 68 с.
12. Методическое пособие по расчету, нормированию и контролю выбросов загрязняющих веществ в атмосферный воздух. – СПб. : НИИ Атмосфера, 2005. – 215 с.
13. Митько, Л. А. Компьютерное моделирование физико-химических процессов в приземном слое атмосферы – необходимый компонент информационного обеспечения в системе эколого-гигиенической безопасности / Л. А. Митько. – Киев : Ин-т проблем моделирования в энергетике НАН Украины, 2005. – 221 с.
14. Никифоров, А. Н. Моделирование полей загрязненности атмосферы в мезометеорологическом пограничном слое / А. Н. Никифоров, Н. С. Бузало // Изв. вузов. Северо-Кавказский регион. Естественные науки. – 2001 (спецвыпуск). – С. 126–128.
15. Предельно допустимые концентрации вредных веществ в воздухе и воде. – Л. : Химия, 1975.
16. Предельно допустимые концентрации (ПДК) загрязняющих веществ в атмосферном воздухе населенных мест. ГН 2.1.6.1338-03.
17. Хоперсков, А. В. Математическое моделиpование экосистем / А. В. Хоперсков // Социальная экология : сборник. – Волгогpад : Изд-во ВолГУ, 1993. – С. 88–91.
18. Хргиан, А. Х. Физика атмосферы / А. Х. Хргиан. – М. : Изд-во МГУ, 1986. – 328 с.
19. Экологический программный комплекс для персональных ЭВМ / под ред. А. С. Гаврилова. – СПб. : Гидрометеоиздат, 1992. – 165 с.
20. Kamenetsky, E. Model of the flow and air pollution concentration in urban canyons / E. Kamenetsky, N. Viern // Boundary Layer Meteorol. – 1995. – V. 73, № 1–2. – P. 203.
This work is devoted to study ground layer pollution dynamics from industrial sources. The mathematical model is constructed for description the nonsteady three dimensional pollutant dynamics at different regimes of nonsteady ejections for a given meteorological atmosphere state. The direct integration of exact advection equations for pollutants is used with taking into account main physical factors. On the basis of developed mathematical model the program complex is created for computational modeling of pollutants dynamics from industrial sources situated at the plants territories.
* Работа выполнена при поддержке гранта РФФИ № 10-07-97017-р_поволжье_а, ГК № 02.740.11.5198.