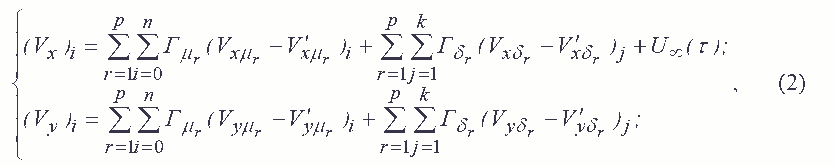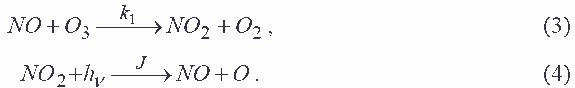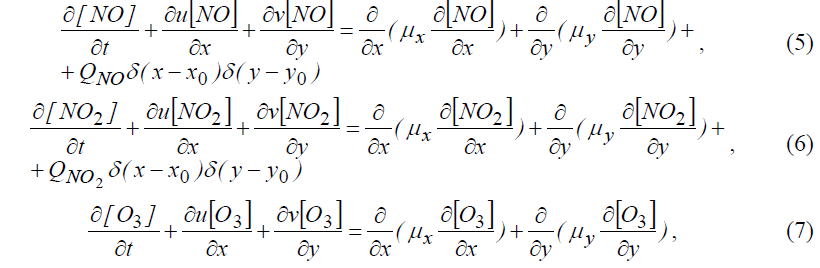Назад в библиотеку
УДК 519.6:504.3.054
Т.И. Русакова*, Н.Н. Беляев**, В.И. Карплюк*
МОДЕЛИРОВАНИЕ ЗАГРЯЗНЕНИЯ АТМОСФЕРЫ НА УЛИЦАХ ГОРОДОВ С УЧЕТОМ ХИМИЧЕСКИХ ПРОЦЕССОВ
Розглянуто задачу розповсюдження забруднюючих речовин на вулиці для схеми розміщення будівель по типу «вуличний каньйон». В роботі побудовано ефективну чисельну модель для прогнозу якості повітряного середовища на вулицях при викидах від автотранспорту. Модель базується на одночасному розв’язку гідродинамічної задачі на основі методу дискретних вихорів та задачі масопереносу про розсіювання газових викидів при русі автотранспорту. Представлено результати чисельних розрахунків. Перевагою розробленої моделі є можливість оперативного розрахунку розсіювання викидів на вулиці з урахуванням хімічних перетворень забруднюючих речовин (окису азоту та двоокису азоту).
Ключові слова: забруднюючі речовини, автотранспорт, метод дискретних вихорів, розсіювання викидів, хімічні перетворення.
Рассмотрена задача распространения загрязняющих веществ на улице для схемы размещения зданий по типу «уличный каньон». В работе построена эффективная численная модель для прогноза качества воздушной среды на улицах при выбросах от автотранспорта. Модель основана на одновременном решении гидродинамической задачи на основе метода дискретных вихрей и задачи массопереноса о рассеивании газовых выбросов при движении автотранспорта. Представлены результаты численных расчетов. Преимуществом разработанной модели является возможность оперативного расчета рассеивания выбросов на улице с учетом химических превращений загрязняющих веществ (окиси азота и двуокиси азота).
Ключевые слова: загрязняющие вещества, автотранспорт, метод дискретных вихрей, рассеивания выбросов, химические превращения.
The task solved for pollutants in the street for the layout the buildings of the type "street canyon". In this work constructed an efficient numerical model for the prediction of air quality in the streets when emissions from automobile transport. The model is based on the solution of hydrodynamic task where was used the method of discrete vortices and on the solution to the task mass transfer of gas dissipation of emissions from automobile transport. The results of numerical calculations presented. The model is the possibility for rapid calculation of dissipation emissions in the street using the chemical reactions pollutants (nitrogen oxide and nitrogen dioxide).
Keywords: pollutants, automobile transport, the method of discrete vortices, dissipation of emissions, chemical transformations.
Постановка проблемы и анализ публикаций. Автомобильный транспорт является одним из наиболее мощных источников эмиссии загрязняющих веществ в атмосферу городов. В настоящее время разрабатываются различные методики и модели для расчета рассеивания выбросов от автотранспорта на улицах. Наиболее часто для решения этой задачи применяются эмпирические модели [4], модели Гаусса [12; 17], численные модели на базе уравнений Навье-Стокса [1; 7; 19]. Эмпирические и аналитические модели дают оценку уровня загрязнения атмосферы без учета влияния зданий на процесс рассеивания загрязняющих веществ. Численные модели, основанные на уравнениях Навье-Стокса, дают возможность учесть влияние зданий, но требуют больших затрат компьютерного времени на практическую реализацию и обоснование той или иной модели турбулентности. Поэтому актуальной задачей является создание численных моделей, позволяющих учесть влияние зданий на рассеивание загрязняющих веществ и, в тоже время, требующих небольших затрат компьютерного времени при практической реализации. Кроме этого, с экологической точки зрения, при расчете качества воздушной среды на улицах, в рамках данного класса задач, важно учесть процессы химической трансформации загрязнителей, выбрасываемых от автомобилей.
Целью данной работы является разработка прикладной численной модели для прогноза уровня загрязнения атмосферы на улицах с учетом химических превращений загрязняющих веществ.
Математическая модель. Рассматривается процесс распространения загрязняющих веществ на улице для схемы размещения зданий по типу «уличный каньон» (рис.1). Для прогноза качества воздушной среды необходимо предварительно решить гидродинамическую задачу по определению поля скорости ветрового потока на улице. Для моделирования процесса обтекания зданий потоком воздуха используется метод дискретных вихрей [2], который дает возможность быстро рассчитать поле скорости ветрового потока в условиях размещения зданий [10]. Решается задача об отрывном нестационарном обтекании двух зданий, характерные размеры первого – l1, h1, второго – l2, h2, расстояние между ними – Δl в плоской системе координат Оху. Поток движется с постоянной скоростью 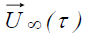 вдоль положительной оси Ох. Параметры h1, h2, l1, l2, Δl могут варьироваться в зависимости от высоты и способа расположения зданий. Для моделирования отрывного обтекания рассматриваемых тел у поверхности земли используется основная и зеркально отображенная вихревые системы [3]. Каждая из них состоит из присоединенных дискретных вихрей, циркуляции которых Γμ равны по величине и противоположны по знаку, и свободных
вдоль положительной оси Ох. Параметры h1, h2, l1, l2, Δl могут варьироваться в зависимости от высоты и способа расположения зданий. Для моделирования отрывного обтекания рассматриваемых тел у поверхности земли используется основная и зеркально отображенная вихревые системы [3]. Каждая из них состоит из присоединенных дискретных вихрей, циркуляции которых Γμ равны по величине и противоположны по знаку, и свободных 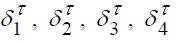 пелен, сходящих с изломов поверхностей в момент времени τ. Движение последних в обеих вихревых системах происходит симметрично. При таком разбиении на линии симметрии 0х автоматически в любой момент времени выполняется условие непротекания, что равносильно присутствию здесь поверхности земли.
пелен, сходящих с изломов поверхностей в момент времени τ. Движение последних в обеих вихревых системах происходит симметрично. При таком разбиении на линии симметрии 0х автоматически в любой момент времени выполняется условие непротекания, что равносильно присутствию здесь поверхности земли.

Рис.1. Схема расчетной области: 1 – здания; 2 – места эмиссии загрязнителей
Схема разбиения поверхностей включает: n контрольных точек, где выполняется граничное условие непротекания и n дискретных вихрей. Первые располагаются на линиях ν, а вторые – на линиях μ между контрольными точками рис.2.
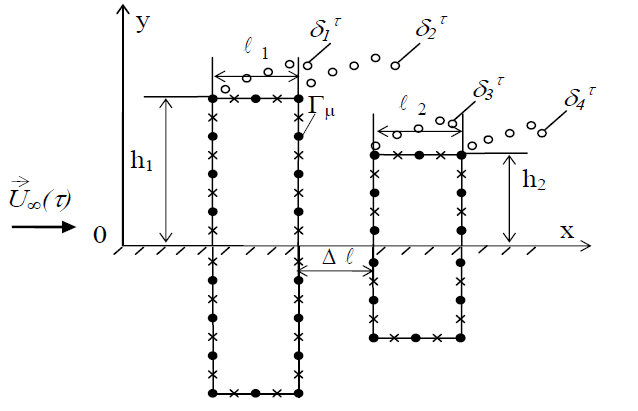
Рис.2. Моделирование поверхности тел системой дискретных вихрей (●) и контрольных точек (×)
Циркуляции присоединенных вихрей Гμ на k-ом шаге по времени определялись из решения системы линейных алгебраических уравнений (1), которая выражает собой условие непротекания поверхности и условие бесциркуляционного обтекания [8; 9].
где Гμ циркуляция μ-ого присоединенного вихря; 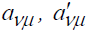 нормальная составляющая скорости в ν-ой контрольной точке от μ-ого присоединенного вихря основной и зеркально отображенной вихревых систем;
нормальная составляющая скорости в ν-ой контрольной точке от μ-ого присоединенного вихря основной и зеркально отображенной вихревых систем; 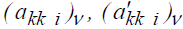 нормальные составляющие скорости в ν-ой контрольной точке от i-ого свободного вихря основной и зеркально отображенной вихревых систем; kk – порядковый номер вихревой пелены; k - количество свободных вихрей в потоке в момент времени τ в соответствующей вихревой пелене kk;
нормальные составляющие скорости в ν-ой контрольной точке от i-ого свободного вихря основной и зеркально отображенной вихревых систем; kk – порядковый номер вихревой пелены; k - количество свободных вихрей в потоке в момент времени τ в соответствующей вихревой пелене kk;  косинус угла между вектором скорости потока
косинус угла между вектором скорости потока 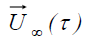 и нормалью
и нормалью 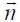 к поверхности тела в каждой контрольной точке. Для первого тела характерна схема разбиения, которая предполагает расположение у поверхности земли контрольных точек, а для второго тела – вихрей, чтобы система алгебраических уравнений (1) была замкнутой.
к поверхности тела в каждой контрольной точке. Для первого тела характерна схема разбиения, которая предполагает расположение у поверхности земли контрольных точек, а для второго тела – вихрей, чтобы система алгебраических уравнений (1) была замкнутой.
Известные значения циркуляций присоединенных дискретных вихрей Гμ в местах излома поверхности определяют циркуляции свободных вихрей Γδ1, Γδ2, Γδ3, Γδ4,сходящих с поверхности тел в момент времени τ.
Для расчета поля скорости используются основные зависимости [3; 10]:
где Γμ - циркуляция μ-ого присоединенного вихря, Γδr – циркуляция свободного вихря r-ой вихревой пелены; U∞(τ) – скорость набегающего потока; Vx i, Vy i – компоненты скорости в рассматриваемой точке плоскости (хi,уi), которые можно рассчитать как сумму соответствующих компонент скорости от всей вихревой системы: присоединенных вихрей μr (компоненты Vxμr, Vyμr) которыми моделируются поверхности зданий, и свободных вихрей δr (компоненты Vxδr, Vyδr), сошедших с острых кромок, на данный момент времени τ основной и зеркально отображенной вихревой системы.
После вычисления поля скорости ветрового потока на улице, решается задача по моделированию рассеивания газовых выбросов на улице при движении автотранспорта. Атомобили выбрасывают различные загрязняющие вещества. В настоящей работе рассматривается процесс химических превращений окиси азота и двуокиси азота. Эти химические превращения могут быть записаны в виде формул [13]:
Чтобы выполнить прогноз уровня загрязнения воздушной среды этими видами загрязнителями нужно решить уравнения переноса (5) – (7):
где QNO – интенсивность выброса NO от автотранспорта, QNO2 – интенсивность выброса NO2от автотранспорта; u, v – компоненты вектора скорости ветра; μ = (μх, μy) – коэффициенты турбулентной диффузии; x0, y0– координаты источника выброса загрязняющего вещества; δ(x - x0), δ(y - y0) – дельта-функция Дирака, с помощью которой моделируется выброс загрязнителя.
Как известно выброс NO2 составляет величину порядка 5% от выброса NOx, а остальная часть выброса, порядка 95% – это выброс NO. Для расчета процесса химической трансформации, необходмо знать скорость химических превращений. Основываясь на анализе зарубежных публикаций [13; 14; 16; 18] в работе принято, что скорость химических превращений составляет: J = 0,0045s-1; k1 = 0,00039ppb-1s-1. Поскольку значение коэффициента k1 приведено не в системных единицах концентрации, то в разработанной подпрограмме расчета химической трансформации осуществляется переход от значений концентрации в [г/м3] к значению в [ppb-1s-1] и обратно. Процесс химической трансформации расчитывается на основе зависимостей (8) – (10) [16; 18].

Метод расчета. Постановка краевых условий для решения уравнения переноса рассмотрена в работах [6; 11]. Для численного интегрирования уравнений (5) – (7) используется попеременно-треугольная неявная разностная схема [1; 5; 7; 15]. Для этого осуществляется расщепление исходных уравнений таким образом, чтобы на разностном уровне неизвестное значение концентрации каждого загрязняющего вещества определялась по методу «бегущего счета».
Практическая реализация модели. Разработанная численная модель была применена для расчета концентрации NO2 на улице при наличии источников эмиссии загрязнителей для схемы «уличный каньон».
Рассматривалось два сценария. Первый сценарий: первое здание ниже по высоте, чем второе (высота первого – 6 м, длина – 16 м; высота второго – 10 м, длина – 12 м). Второй сценарий: первое здание выше второго (высота первого – 12 м, длина – 16 м; высота второго – 6 м, длина – 12 м). На улице располагалось два источника выброса NOx интенсивностью Q = 10 г/(м⋅с), первый располагался непосредственно возле первого здания, а второй – между двумя зданиями. Расчет выполнялся при следующх исходных данных: скорость ветра – 6 м/с; коэффициенты атмосферной диффузии μх=μy=3,5м2/с; размеры расчетной области: длина – 125 м, высота – 42 м. В качестве начального условия задавалось, что фоновая концентрация NO и NO2 в расчетной области равна нулю, а концентрация O3 принята равной 0,16 мг/м3. Результаты расчета представлены на рис. 3 – 4.
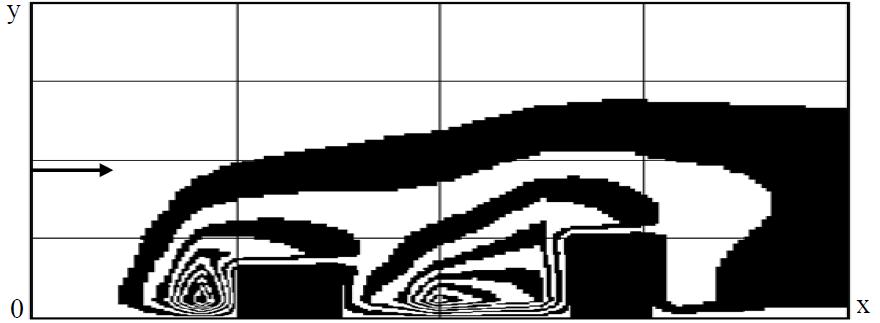
Рис.3. Распределение концентрации NO2 на улице в момент времени t=12,5 c (первый сценарий)

Рис.4. Распределение концентрации NO2 на улице в момент времени t=12,5 c (второй сценарий)
Как видно из представленных рисунков на улице четко выделяются две подзоны с большим градиентом концентрации – места расположения источников эмиссии, а формирующаяся зона загрязнения охватывает оба здания. Это означает, что NO2 будет поступать вовнутрь помещений каждого здания через неплотности и за счет работы вентиляции. Для обоих сценариев наблюдается наиболее интенсивное загрязнение на наветренной стороне первого здания, особенно до уровня 6 м от земли. Концентрация NO2 возле второго здания достаточно сильно повышена на высоте порядка 4м от уровня земли. Время расчета одного варианта задачи составляет 8 с.
Таким образом, на основе разработанной модели имеется возможность оперативно прогнозировать уровень загрязнения атмосферы на улицах с учетом химических превращений загрязнителей.
Выводы. В работе построена эффективная численная модель для прогноза качества воздушной среды на улицах при выбросах от автотранспорта. Достоинством разработанной модели является возможность оперативно рассчитывать рассеивание выбросов на улице с учетом химических превращений загрязняющих веществ. Модель может быть использована на практике при планировании магистралей улиц, в новых районах городов или при реконструкции старых. Дальнейшее развитие модели следует проводить в направлении ее адаптации к 3D моделированию.
Библиографические ссылки
1. Антошкина Л. И. Моделирование аварийных ситуаций на промышленных объектах и безопасность жизнедеятельности / Л. И. Антошкина, Н. Н. Беляев, Л. Ф. Долина, Е. Д. Коренюк – Днепропетровск, 2011. – 123 с.
2. Белоцерковский С. М. Моделирование отрывного обтекания цилиндра вблизи экрана / С. М. Белоцерковский, В. Н. Котовский, М. И. Ништ // ИФЖ. – 1986. – Т.50, № 2. – C. 78 – 84.
3. Белоцерковский С. М. Математическое моделирование плоскопараллельного отрывного обтекания тел / С. М. Белоцерковский, В. Н. Котовский, М. И. Ништ – М., 1988. – 232 с.
4. Бруяцкий Е. В. Теория атмосферной диффузии радиоактивных выбросов / Е. В. Бруяцкий – Киев: Институт гидромеханики НАН Украины, 2000. – 443 с.
5. Згуровский М. З. Численное моделирование распространения загрязнения в окружающей среде / М. З. Згуровский, В. В. Скопецкий, В. К. Хрущ, Н. Н. Беляев – Киев, 1997. – 368 с.
6. Марчук Г. И. Математическое моделирование в проблеме окружающей среды / Г.И. Марчук – М., 1982. – 316 c.
7. Пшинько А. Н. Моделирование загрязнения атмосферы при техногенных авариях / А. Н. Пшинько, Н. Н. Беляев, П. Б. Машихина. – Дніпропетровськ, 2011. – 168 с.
8. Русакова Т. И. Численное исследование структуры вихрового потока около высотных сооружений / Т. И. Русакова, В. И. Карплюк // Вісник Дніпропетр. ун - ту. Серія «Механіка». – 2006. – Вип.10, т. 1. – С. 154 - 160.
9. Русакова Т. И. Задача численного расчета обтекания зданий воздушным потоком / Т. И. Русакова, В. И. Карплюк // Вісник Дніпропетр. ун - ту. Серія «Механіка». – 2007. – Вип.11, т. 1. – С. 53 – 58.
10. Русакова Т. И. Исследование поля скоростей при обтекании зданий воздушным потоком / Т. И. Русакова, В. И. Карплюк // Вісник Дніпропетр. ун - ту. Серія «Механіка». – 2008. – Вип.12, т. 1. – С. 41 – 49.
11. Самарский А. А. Теория разностных схем / А. А. Самарский – М., 1983. – 616 с.
12. Шаталов А. А. Методика расчета распространения аварийных выбросов, основанная на модели рассеивания тяжелого газа / А. А. Шаталов, М. В. Лисанов // Безопасность труда в промышленности. – 2004. – № 9. – С. 46 – 52с.
13. Berkowicz R. A Simple Model for Urban Background Pollutio / R. Berkowicz // Environmental Monitoring and Assessment. – 2000. – Vol. 65. – P. 259 – 267.
14. Berkowicz R. Street Scale Models / R. Berkowicz, J. Fenger, O. Hertel, F. Palmgren // Urban Air Pollution – European Aspects, Kluwer Academic Publishers. – 1998. – P. 223 – 251.
15. Biliaiev M. M. Numerical simulation of indoor air pollution and atmosphere pollution for regions having complex topography / M. M. Biliaiev, M. M. Kharytonov // Conference Abstracts of 31st NATO / SPS International Technical Meeting on Air Pollution Modelling and it’s Application, 27 September – 01 October, Torino, Italy, 2010. № P 1.7.
16. Denby Br. Modelling of Nitrogen Dioxide (NO2) for air quality assessment and planning relevant to the European Air Quality Directive / Br. Denby, I. Douros // Fragkou, 2010. – P. 167 – 174.
17. Hanna S. Air Quality Modeling Over Short Distances / S. Hanna // College on Atmospheric Boundary Layer and Air Pollution Modeling: 16 May-3 June 1994. №SMR/760-2. – P. 712 – 743.
18. Hertel O. Modelling NO2 concentrations in a street canyon / O. Hertel, R. Berkowicz // DMU Luft A-131, 31 p. NERI, P.O. Box358, DK 4000 Roskilde, Denmark.
19. Murakami S. Comparison of “k-?” model, ASM and LES with wind tunnel test for flow field around cubic model / S. Murakami, A. Mochida, H. Yoshihiko // 8th Intern. Conf. on Wind Engineering, Western Ontario, July 8-11, 1991. – № 12 – 3.
Надійшла до редколегії 01.11.2013.
*Днепропетровский национальный университет им. Олеся Гончара
**Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна
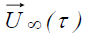 вдоль положительной оси Ох. Параметры h1, h2, l1, l2, Δl могут варьироваться в зависимости от высоты и способа расположения зданий. Для моделирования отрывного обтекания рассматриваемых тел у поверхности земли используется основная и зеркально отображенная вихревые системы [3]. Каждая из них состоит из присоединенных дискретных вихрей, циркуляции которых Γμ равны по величине и противоположны по знаку, и свободных
вдоль положительной оси Ох. Параметры h1, h2, l1, l2, Δl могут варьироваться в зависимости от высоты и способа расположения зданий. Для моделирования отрывного обтекания рассматриваемых тел у поверхности земли используется основная и зеркально отображенная вихревые системы [3]. Каждая из них состоит из присоединенных дискретных вихрей, циркуляции которых Γμ равны по величине и противоположны по знаку, и свободных 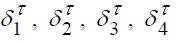 пелен, сходящих с изломов поверхностей в момент времени τ. Движение последних в обеих вихревых системах происходит симметрично. При таком разбиении на линии симметрии 0х автоматически в любой момент времени выполняется условие непротекания, что равносильно присутствию здесь поверхности земли.
пелен, сходящих с изломов поверхностей в момент времени τ. Движение последних в обеих вихревых системах происходит симметрично. При таком разбиении на линии симметрии 0х автоматически в любой момент времени выполняется условие непротекания, что равносильно присутствию здесь поверхности земли.


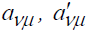 нормальная составляющая скорости в ν-ой контрольной точке от μ-ого присоединенного вихря основной и зеркально отображенной вихревых систем;
нормальная составляющая скорости в ν-ой контрольной точке от μ-ого присоединенного вихря основной и зеркально отображенной вихревых систем; 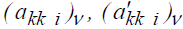 нормальные составляющие скорости в ν-ой контрольной точке от i-ого свободного вихря основной и зеркально отображенной вихревых систем; kk – порядковый номер вихревой пелены; k - количество свободных вихрей в потоке в момент времени τ в соответствующей вихревой пелене kk;
нормальные составляющие скорости в ν-ой контрольной точке от i-ого свободного вихря основной и зеркально отображенной вихревых систем; kk – порядковый номер вихревой пелены; k - количество свободных вихрей в потоке в момент времени τ в соответствующей вихревой пелене kk;  косинус угла между вектором скорости потока
косинус угла между вектором скорости потока 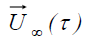 и нормалью
и нормалью 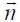 к поверхности тела в каждой контрольной точке. Для первого тела характерна схема разбиения, которая предполагает расположение у поверхности земли контрольных точек, а для второго тела – вихрей, чтобы система алгебраических уравнений (1) была замкнутой.
к поверхности тела в каждой контрольной точке. Для первого тела характерна схема разбиения, которая предполагает расположение у поверхности земли контрольных точек, а для второго тела – вихрей, чтобы система алгебраических уравнений (1) была замкнутой.