Оптимизация эффективности Марковских моделей в моделировании компьютерных сетей.

Перевод: А.В. Стретович

Источник оригинала статьи : http://www.iaeng.org/publication/WCECS2009/WCECS2009_pp367-371.pdf

Авторы оригинала: Nisrine Sinno, Hussein Youssef, Ghaddar Ahmad

 

 

Аннотация – Эта статья посвящена применению дискретной Марковской модели [1], [2] для моделирования компьютерных сетей при постоянном количестве клиентов. При работе применяются два численных метода, метод степенного моделирования и p-метод. Были использованы две сетевые модели: модель Гордана – Ньюэлла и модель Кокса-Кокса. В ходе исследования этих двух моделей в качестве критерия приближения к стационарному состоянию использовалась их асимптотическая погрешность

 

Ключевые слова – Компьютерные сети, Дискретные Марковские Цепи, оценка эффективности, P-моделирование, Степенное моделирование

Введение

Компьютерные сети относятся к классу физических систем которые могут быть эффективно изучены с помощью "дискретно-событийного" моделирования. В качестве объекта моделирования компьютерных сетей были выбраны закрытая сеть Гордана- Ньюэлла (“Gordan-Newell network”) и сеть Кокса-Кокса (“Cox-Cox network”) с постоянным числом клиентов.

Учитывая тот факт, что сеть описана с помощью численных значений поведения, компьютерная сеть подпадает под категорию поведения без запоминания, потому что знание настоящего отделяет прошлое от будущего. При этом изучение поведения компьютерных сетей с помощью Марковских цепей вполне обосновано, ввиду того, что Марковская цепь – это особенный стохастический процесс, в котором будущее вероятное поведение процесса уникально определенно его текущим состоянием.

Составляющие сети, такие как поведение при доступе к сети, могут быть описаны как дискретные связанные события. В ходе моделирования будут применены два типа моделей Марковских цепей, Степенной Марковский процесс (Power Markov process) и Марковский процесс P-моделирования в пространстве дискретных событий.

Для того, чтобы узнать, какой из методов надежнее для создания сетевых моделей Гордана Ньюэлла и Кокса-Кокса, будут сравниваться приближения к стационарному состоянию обоих методов.

Имитационное моделирование

 

А) Марковская модель для дискретного времени

Марковская модель для дискретного времени определяется набором вероятностей перехода между дискретными состояниями модели. Переходы связаны с вероятностями переходов между состояниями.

 

Вероятностные переходы NxN между N состояниями называются матрицей переходов P (the Transition Probability Matrix P).

Если P0 – первоначальный вероятностный вектор, тогда после k шагов вероятность состояния определяется вектором:  π_k =P0* P ^k

Матрица Pk - это k –ая переходная матрица после умножения P на саму себя k раз.

В установившемся режиме при умножении Р на текущий вероятностный вектор Р не ожидается каких-либо других изменений в вероятностях состояний, ввиду того, что Марковская цепь эргодична [3]. Вектор вероятностей в установившемся режиме для всех состояний Марковской модели определяется как:

Π x P= Π                                       (2)

Это уравнение будет использоваться вместе с условием:          

∑ π_i  = 1                                    (3)

для того, чтобы определить все вероятности установившегося режима для выбранных сетевых моделей. 

B)  Gordan-Newell Network [4]

Это сеть, разработанная для постоянного числа клиентов. Количество возможных состояний ограничено. Сеть состоит из нескольких узлов. Пусть m – число узлов, а  n – постоянное число пакетов, циркулирующих по сети, посылаемых  n разными клиентами, тогда N возможных состояний определяется как:

               (4)

 

Набор возможных состояний для сети из трех узлов определяется как:

E={(i,j,k)∈ N 3 , i+j+k = n}          (5)

При m=3 для n пакетов  число состояний будет равно:

Сетевая модель Гордана- Ньюэлла приведена ниже на рисунке 1.

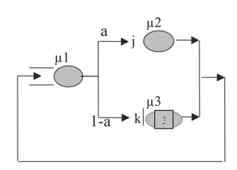
Рисунок 1. модель Гордана- Ньюэлла с n=i+j+k

 

Количество состояний резко растет с увеличением n. Если число пакетов, обращающихся к узлам сети, равно 2, то число состояний будет равно 6. Эти состояний будут распределены между тремя узлами:

(2,0,0),(1,1,0),(0,2,0) ,(1,0,1),(0,0,2),(0,1,1).

 

Для стохастический переменной a в пределах (0<a<1), в промежуток времени [t, t+1] переменная Бернулли с параметром a - это число пакетов, пытающихся получить доступ к сети.

Определяя A(t)=1 как число пакетов, получающих доступ к узлу в промежуток времени [t,t+1], и A(t)=0 как число пакетов, не получающих доступ в этом промежутке, вероятность доступа A(t) пакетов к одному узлу будет равна:

P[A(t) =1] = a       (7)

 

А вероятность отсутствия A(t) пакетов, получающих доступ к узлу, будет

P[A(t)=0] = 1-a.    (8)

На Рис.1 в сети из трех узлов i будет числом пакетов, приходящих на узел 1 с вероятностью µ1, j будет числом пакетов, приходящих на узел 2 с вероятностью µ2, а k будет числом пакетов, приходящих на узел 3 с вероятностью µ3.

Общее число пакетов в сети постоянно и равно n=i+ j+ k. Пакет на узле 1 может уйти на узел 2 с a или перейти на узел 3 с вероятностью 1- a, пакеты на узле 2 могут перейти на узел 1 с вероятностью 1, пакеты с узла 3 могут переместиться на узел 1 с вероятностью 1.

 

Диаграмма состояний для сети Гордана-Ньюэлла с двумя пакетами(клиентами) представлена на рисунке 2. 

Рисунок 2. Диаграмма состояний для сети Гордана-Ньюэлла с двумя пакетами(клиентами)

 

Для того, чтобы создать алгоритм для запоминания состояний узла I в заданный момент времени t, мы принимаем Xti как число клиентов в заданный момент в узле I, а вектор Xt = (Xt 1, Xt 2, Xt 3) представляет собой набор клиентов, находящихся в сети в узлах 1,2,3 в момент времени t.

 

Первая теорема: Xt – конечен, гомогенен, минимален[1].

 

Вторая теорема: вектор вероятностей для установившегося режима для любого состояния I (i,j,k)  расчитывается как:

               (9)

При условии, что

                        (10)

Если Di определяет среднее число клиентов, обращающихся к узлу i, то

D1 = D2 + D3, D2 = a.D1, D3 = (1-a).D1                (11)

 

Эта система линейна, гомогенна и минимальна, у нее есть по крайней мере одно решение. Одно из решений такой системы: ( x, ax, (1-a)x ).

 

Вероятность установившегося режима для среднего числа клиентов  x на узле 1, a*x на узле  2, (1-a)*x на узле 3 соответственно :

                       (12)

 

Пусть матрица вероятностей установившегося режима Q[N, N], с N=6 состояниями для Гордана- Ньюэлла с двумя пакетами (см Рис.2) будет иметь размерность [6,5] . В каждой строке матрицы один элемент столбца будет нулевым.

Если каждое состояние I определяется i и j, то k вычитается из i , j , n

k = n-(i+j)                  (13)

 

Для имитационной модели сети по методам Степенного и

P-моделирования был составлен алгоритм преобразования состояния I в форму (i,j) и из формы (i,j) в состояние I (выделение линии, затем столбца, затем линии с ограничением, затем столбца с ограничением).  Будем увеличивать I от 0 до N-1 путем увеличения i от 0 до N и увеличения j от 0 до N-i.)

В этой модели сеть имеет постоянное число клиентов, но матрица вероятностей перехода P изменяется в зависимости от заданного коэффициента.

Модель представлена на рисунке 3, это сервер “Coaxian” представляющий две компьютерные сети A, B с заданным коэффициентом λ и числом узлов m для A, а также коэффициентом µ числом узлов n для сети B. Имитационное моделирование в таком случае показывает эффективность конвергенции в предельных случаях организованной вероятностной матрицы переходов и распределенной путем изменения значений коэффициентов.  

 

Тестирование и Результаты

Моделирование сети Гордана-Ньюэлла

Были проведены тесты, используя свыше 10000 наборов стохастических данных. Рисунки [4] [5] [6] [7] показывают, что метод P-моделирования более эффективен, чем метод Степенного моделирования, т.к. P-моделирование обеспечивает более быструю сходимость к стационарному режиму.

Рисунок 3. Диаграмма состояний для сервера Coaxian (с двумя сетями A,B)

 

Теоремы:

Вероятностная матрица установившегося режима для А:

         (14)

    (15)

    (16)

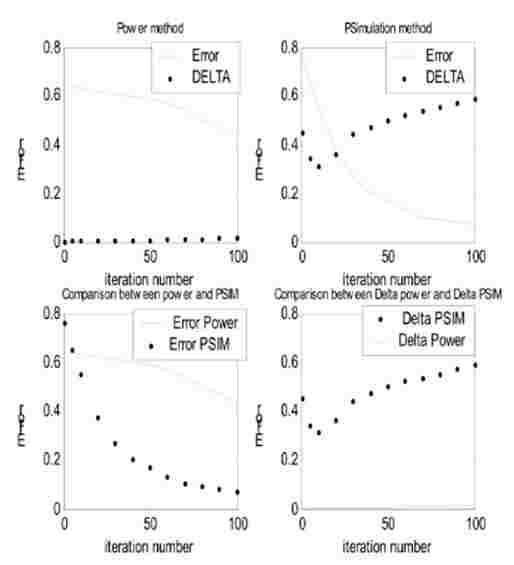
Рисунки  [4][5][6][7] Сравнение между Степенным и P-моделированием сети Гордана-Ньюэлла с двумя клиентами.  

Имитационная модель Кокса-Кокса

Путем изменения коэффициентов было составлено несколько моделей сетей Кокса-Кокса. Три имитационные модели

Показаны на рисунках  8,9,10: Нормальная модель сети на рисунке 9, организованная модель на рисунке 10 и распределенная на 8 соответственно.  Матрицы вероятностей стационарного режима πA и π B рассчитаны с помощью Марковских цепей Степенным и P-моделированием [6, 7].

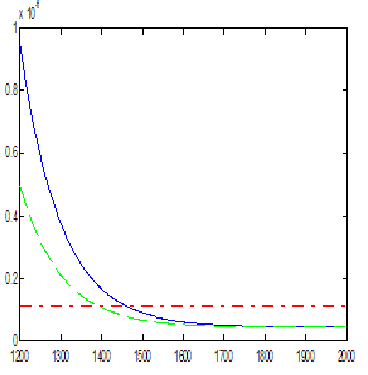
Рисунок 8. Погрешность в распределенной модели

 

 

Рисунок 9. Погрешность в нормализированной модели

 

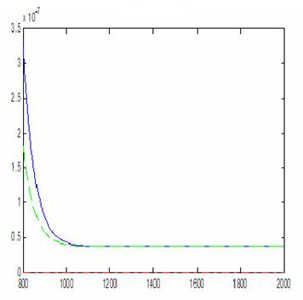
Рисунок 10. Погрешность в организованной модели

 

Первый вывод, который можно сделать, состоит в том, что коэффициенты играют значительную роль:  

Случай распределенной модели Кокса-Кокса (рис. 8): Степенной метод быстро сходится на ранних итерациях, но метод Р-моделирования обеспечивает более точные результаты, ошибка по окончанию итераций меньше чем в случае метода Степенного моделирования.  

Случай организованной модели Кокса-Кокса (рис. 10): В этой модели Степенной метод сходится к установившемуся режиму быстрее чем метод Р-моделирования. Но по сравнению с результатами распределенной модели (рис. 8) сходимость происходит намного медленнее.

Случай нормальной модели Кокса-Кокса (рис. 9): По этой модели можно сделать вывод, аналогичный случаю распределенной модели, но с нормализованным методом степенного моделирования сходимость получается точнее, чем в методе Р-моделирования.

Эти результаты позволяют сделать вывод о том, что:

Организованная имитационная модель менее конвергентна, чем распределенная и нормальная.

Нормализованный метод степенного моделирования дает более точные результаты, чем тот же метод без нормализации.

Из-за того, что нормализация не применима в случае методов Р-моделирования, избежать погрешности, как в случае с методом степенного моделирования, невозможно. Поэтому нормализованный метод степенного моделирования предпочтительнее в модели Кокса-Кокса.

Для того, чтобы подтвердить эти выводы, результаты моделирования были получены с использованием Matlab и C++ на 100 итерациях в случае нормальной модели Кокса-Кокса. Были получены такие результаты:  Errpsim (matlab) < Errpower (Matlab) without normalization

•  Errpsim (C++)   < Errpower (C++) без нормализации

Errpower (C++) с нормализацией < Errpower(Matlab) с нормализацией

Таким образом, для некоторых моделей погрешность в нормализованном методе степенного моделирования меньше, чем в случае использования метода Р-моделирования, но это утверждение нельзя применить ко всем моделям.

 

 Заключение

Эта статья описывает сравнение асимптотической эффективности методов Степенного и Р-моделирования для нескольких классов сетей, сети Гордана-Ньюэлла и разных видов моделей Кокса-Кокса. Анализ результатов дает возможность сделать следующие заключения:

Скорость схождения Р-моделирования зависит от состояния, взятого из заданного набора состояний. 

Р-моделирование дает лучшую сходимость к точному решению по сравнению со Степенным методом.

Нормализация метода Степенного моделирования в случае распределенной модели Кокса-Кокса эффективнее метода Р-моделирования.

Увеличение асимптотической эффективности в Марковских цепях остается открытой проблемой. Методы имитационного моделирования, предложенные в данной работе, помогают лучше понять их поведение по результатам моделирования компьютерных сетей на Марковских цепях. Однако, необходимо провести больше тестов на других типах сетей для оценки использованные методы моделирования.

 

 

Перечень ссылок

 

Bloch, Grenier, Hermann and Trivedi, « Queuing Network and Markov Chain », J. Wiley ed. 1998.

A.Bouillard.  « Optimisation  et  analyse  probabiliste  de  systèmes  à

événements  discrets ». PhD thesis, ENS Lyon, France, 2005.

P.Fernandes.« Méthodes numériques pour la solution de systèmes Markoviens à grand espace d'états ». PhD thesis, INPG, Grenoble, France, 1998.

Kishor, Shridharbhai and Trivedi, « Probability & statistics with reliability queuing and computer science applications », PRENTICE-HALL, INC., Englewood Cliffs, New Jersey 07632.

William J. Stewart. « Introduction to the numerical solution of Markov Chains». Princeton University Press, new Jersey 1994.

Pellaumail, Boyer, Leguesdron « Réseaux ATM et P-simulation ».

A.Bouillard. « Optimisation et analyse probabiliste de systèmes à événements discrets ». PhD thesis, ENS Lyon, France, 2005.