Статья опубликована в №3 (ноябрь) 2013

Источник статьи http://sci-article.ru/stat.php?i=modelirovanie_rabotY_vYchislitelnogo_klastera_na_primere_LANL_CM5

Разделы: Информационные технологии, Математика
Размещена 30.11.2013. Последняя правка: 03.12.2013.

МОДЕЛИРОВАНИЕ РАБОТЫ ВЫЧИСЛИТЕЛЬНОГО КЛАСТЕРА НА ПРИМЕРЕ LANL CM5

Гаевой Сергей Владимирович

ВолгГТУ

аспирант

Аль-Хадша Фарес Али Хуссейн, ВолгГТУ, кафедра

 

Ключевые слова:

Вычислительный кластер, rigid jobs, имитационное моделирование.

Keywords:

Computing cluster, rigid jobs, simulation modeling, simulation.

Аннотация:

В связи с массовым распространением распределенных вычислительных систем стала актуальной проблема их эффективного использования. Поэтому необходим анализ обслуживания заданий конкретным кластером. Наша кафедра имеет кластер, работу которого мы собираемся промоделировать в дальнейшем.

 

Abstract:

Due to wide spread of the distributed computing systems a problem of its effective usage became actual. Therefore the analysis of computing incoming jobs by some cluster system is necessary. Our chair has a cluster which functioning we are going to simulate in the future.

 

УДК 004.94

ВВЕДЕНИЕ

Проблема параллельных и высокопроизводительных вычислений довольно актуальна в современное время [1]. В частности она затрагивает такие системы, как кластера и Гриды (Grids). В данной работе мы затронем вопрос моделирования работы кластера. Каждый кластер построен из вычислительных машин. С практической точки зрения [1] крайне удобно создавать кластеры так, чтобы машины внутри обладали одинаковыми характеристиками производительности, поэтому реальные кластера построены по такому (или в большинстве своем по такому) принципу [1]. Рассматривать иные ситуации в данном контексте не имеет смысла.

В ИСП РАН в рамках работ по параллельным вычислениям и Grid-технологиям разрабатывается среда моделирования распределенных вычислительных систем [2].

АППРОКСИМАЦИЯ И МОДЕЛИРОВАНИЕ

1 Постановка задачи

Во многих работах, к том числе и тех, которые будут рассмотрены ниже делались попытки аппроксимации потоков входных заданий различных кластеров или групп кластеров с различной степенью точности. В данной работы ставится целью — рассмотреть функционирование вычислительной системы как системы массового обслуживания (СМО) при использовании различных аппроксимаций.

Каждое задание может исполняться параллельно на нескольких машинах. Количество вычислительных машин, на которых исполняется заданий называется шириной [2]. Длиной задания назовем время его выполнения. Площадью задания назовем произведение длины на ширину. Очевидно, что площадь — это сложность задания. Она же — суммарное машинное время обслуживания. Различные авторы придерживаются различной терминологии.

Изначально процессоры были одноядерными, поэтому в качестве элемента вычислительной системы принимали именно отдельный процессор (несколько процессоров могут располагаться на одной плате). Однако сейчас каждое ядро можно рассматривать как вычислительную машину. То есть в кластере на разных ядрах одного процессора могут выполняться разные задачи.

В данной работе кластер будет представлен в виде обслуживающего блока с единой неприоритетной, не ограниченной по размеру очередью. Это обеспечит нам обслуживание всех входящих заданий. При завершении исполнения очередь просматривается вся от начала до конца, так как извлекаемых заданий быть несколько (ведь ушедшее задание может освободить несколько каналов). Задание, для которого достаточно свободных машин, ставится на исполнение, и просмотр очереди продолжается со следующего за ним задания.

Длиной очереди назовем количество, находящихся в ней заданий. Шириной (сложностью, площадью) очереди — сумму ширин (сложностей, площадей) входящих в нее заданий.

Будут определены следующие параметры СМО:

• использование кластерной системы;
• среднее число используемых узлов (занятых каналов);
• среднее число заданий под обслуживанием;
• средняя длина очереди;
• среднее число заданий в системе;
• среднее время пребывания задания в системе;
• среднее время ожидания в очереди;
• среднее время обслуживания.

Часть параметров дублирует друг друга (например, среднее число заданий в системе равно сумме средней длины очереди и среднее число заданий под обслуживанием). Это сделано с целью контроля моделей.

2 Используемые законы распределения

Для описания моделей СМО будет использована собственной модификацией нотации Кендалла [3]. В качестве законов распределения случайных величин будут взяты величины, распределенные по гипергамма-закону [4].

Классическая модель СМО без изменений не подойдет, так как она подразумевает, что задания выполняются одним каналом обслуживания. В нашем случае задания могут занимать несколько каналов обслуживания.

Существуют два подхода к этому вопросу. [5] вводит два вида входящих заданий: «rigid» и «moldable». Первый тип имеет фиксированную ширину на момент прихода, второй же позволяет системе самой выбрать ширину при заданной сложности (площади). Здесь будет рассматриваться исключительно первый вариант.

Также необходимо учесть, что ширину и длину задания (или ширину и площадь) в общем случая нельзя рассматривать как независимые величины. Так как ширина может принимать конечное число значений, вероятность того, что задание обладает некоторой шириной, можно определить в виде массива значений. Для КАЖДОЙ ширины нам потребуется использовать свое распределение длины задания. Законы этих распределений могут быть различными, но мы для удобства будем полагать их одинаковыми, но различающимися по параметрам.

Чтобы показать, что заданий выполняется параллельно, мы будем ставить после обозначения закона распределения знак «^». Чтобы показать, что величина имеет свои параметры закона распределения для заданий различной ширины, буде предварять обозначение этого закона распределения знаком «$».

Таким образом, простейшая модель СМО будет обозначаться как HΓ/$HΓ^/n/m.

3 Подход к моделированию

[5] предоставляет логи работы реальных вычислительных систем. В логах указывается в том числе время приходя задания, его длина и ширина. Задания, для которых не указан хотя бы один из этих параметров, необходимо вывести из рассмотрения. Приход первого заданий происходит в момент времени, принятый за ноль. Время моделирования положим равным времени прихода последнего задания (это выводит из рассмотрения последнее задание, но при большом их числе это не должно сказаться на результате).

Моделирование будем вести методом имитационного моделирования, методом дискретных событий. Таким образом, можно промоделировать лог, используя время прихода, длину и ширину заданий. Это даст нам искомые параметры. Такие модели известны как детерминированные имитационные модели [6][7].

После осуществления аппроксимации необходимо провести моделирование стохастической модели со случайными моментами прихода заданий со случайными параметрами. Очевидно, что результат моделирования тоже станет случайным. Поэтому много раз промоделируем случайные исходы работы системы, а затем соберем статистику и по ней оценим требуемые параметры с достаточной степенью точности. В соответствии с Центральной предельной теоремой (ЦПТ) рассчитаем погрешность. В качестве доверительной вероятности возьмем 99,73%, т. е. используем правило трех сигм [6][7].

Во всех имитационных экспериментах число испытаний было выбрано так, чтобы относительная максимальная погрешность не превышала 5%. Поскольку имеется набор измеряемых данных, для многих из низ получалось погрешность порядка процента.

Фактически лог является одним из бесконечного числа вариантов функционирования стохастической. В силу стационарности и эргодичности этого процесса его характеристики должны быть близки к характеристикам стохастической модели [6]. Это дает нам возможность проверить работоспособность модели.

В качестве примера мы будем анализировать работу кластера LANL CM5 на основе лога LANL-CM5-1994-4.1-cln.swf. Очищенные от спорных данных логи (cln) рекомендуются сайтом для научных изысканий, поэтому в дальнейшем мы использовали именно такой. Все задания этого кластера имеют ширины 32, 64, 128, 256, 512 или (очень редко) 1024. Из 122,060 заданий, указанных в логе, были отброшены только три по причине отсутствия необходимой информации.

4 Предложенные модели

Принцип синтеза модели СМО подробно рассмотрен, например, в [8] и [9], поэтому остановимся лишь на особенностях:

1. В системе имеется несколько каналов обслуживания и заявка может занимать сразу несколько каналов.
2. Очередь просматривается по особо схеме, изложенной ранее. В частности, в отличие от модели [9] у нас нет отказов в обслуживании из-за неограниченности очереди.

Все ниже предложенные модели различаются лишь способом представления потока входящих заявок, поэтому акцент будет сделан именно на нем.

4.1 Почти классическая модель

В первую очередь необходимо рассмотреть самую простую модель — модель, отличающуюся от классической лишь параллельностью исполнения. То есть модель HΓ/$HΓ^/1024, в которой имеется единый стационарный поток входных заданий.

В качестве приближенных значений вероятностей появления заданий конкретной ширины использовались доли заданий соответствующей ширины из лога работы кластера. Будет также полагать, что ширины приходящих заданий являются независимыми.

4.2 СМО с разделением потока заявок по ширине

В [10][11][12] использовался подход с использованием гиперэрланговского распределения (частный случай гипергамма-распределния). Возможные значения ширины заданий разделялись на интервала (например, с 64 по 126, со 127 по 161 и т. д.). Для каждого интервала определялись свои параметры распределения длины заданий. Для каждого интервала существовал свой входной поток заданий. Все эти потоки принимались независимыми и гиперэрланговскими.

Чтобы показать, что модель использует разделенные потоки входных заданий, будем ставить $ перед законом распределения времени между входящими заданиями, то есть $HΓ/$HΓ^/1024.

4.3 СМО с нестационарным потоком входных заявок

Альтернативный подход заключается в рассмотрении потока входных заявок как нестационарного пуассоновского. В [13][14] рассматривалось изменение потока заявок в течение дня. В данной работе будет рассмотрено изменение интенсивности потока заявок в течение недели. На рисунке 1 видна явная зависимость интенсивности входных заявок от времени в течение недели.

Рисунок 1 — Изменение интенсивности потока заявок в течение недели

 

Как мы видим на рисунке 1, наблюдается сильное изменение интенсивности. Оно обусловлено режимом трудовой недели.

Из [6] нам известно: вероятность того, что на некотором отрезке не будет событий пуассоновского потока, определяется законом Пуассона и равняется:

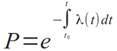, (1)

где t₀ - левый конец отрезка, t - правый конец отрезка, λ(t) - интенсивность событий, P - вероятность отсутствия событий на отрезке.

В соответствии с [6], случайное время до следующего события можно получить путем решения уравнения:

, (2)

где t₀ - точка отсчета (обычно предыдущее событие), t - искомое время, λ(t) - интенсивность событий, R - случайная величина, равномерно распределенная по полуинтервалу (0;1].

Теория вероятности говорит, что вероятность попадания случайного абсолютно непрерывного значения в конкретную точку равна нулю. Однако при компьютерном моделировании такое возможно. Экспонента ни при каких значениях конечных показателях степени (в том числе и комплексных) не обращается в нуль. Значит, это сделает уравнение неразрешимым.

Вышеуказанное уравнение эквивалентно следующему:

. (3)

В правой стороне этого уравнения находится случайная величина, распределенная по экспоненте, с единичным математическим ожиданием. В [15][16] вместо экспоненциально распределенной величины предлагается использовать другие. То есть уравнение преобразуется в

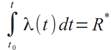, (4)

где R^* - неотрицательная случайная величина с единичным матожиданием.

Очевидно, что при λ(t) = λуравнение преобразуется к виду

, (5)

а решение имеет вид

, (6)

что соответствует рекуррентному потоку событий Пальма, причем R^*/λ является временем между событиями (со средним значением 1/λ).

Назовем величину R^* приведенным временем между приходами заданий.

Чтобы показать, что модель использует нестационарные потоки входных заданий, будем ставить ~ перед закона распределения времени между входящими заданиями. Обозначим эту модель как ~HΓ/$HΓ^/1024.

4.4 СМО с разделением нестационарных потоков входящих заявок по ширине

Логичным продолжением является объединение идеи разделения потоков входных заданий и идеи нестационарности. Стоит отметить, что у каждого потока заданий будет своя интенсивность (рис. 2). Очевидно, что доминирует ширина 32. Разное соотношение интенсивностей в некоторые моменты времени означает разную вероятности прихода заданий разной ширины в эти моменты. То есть в данной модели вероятности прихода заданий некоторой ширины также является функцией времени в течение недели.

Будем обозначать эти модели префиксом $~. Положение знака $ перед ~ означает, что у каждого потока будет своя функциональная зависимость интенсивности от времени. То есть $~HΓ/$HΓ^/1024.

4.5 Упрощение СМО с разделением нестационарных потоков входящих заявок по ширине

По рисунку 2 видно, что интенсивность появления заданий шириной 64 примерно пропорциональна интенсивности появления заданий шириной 32, поэтому логично отбросить зависимость вероятность появления задания определенной ширины от времени суток. В этом случае можно сделать допущение

, (7)

где λ_i(t) - интенсивность появления заданий i - й ширины, λ(t) - интенсивность появления заданий, γ_i - вероятность появления (доля) заданий i- й ширины.

Оно позволяет нам не рассчитывать и не хранить интенсивность прихода заявок определенной ширины, а оценивать их, исходя из этого приближения.

Будем обозначать эти модели префиксом ~$. Положение знака $ после ~ означает, что на все потоки задается одна функциональная зависимость интенсивности от времени. То есть ~$HΓ/$HΓ^/1024. 

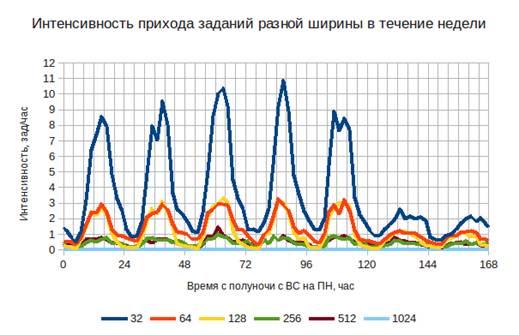
Рисунок 2 — Изменение интенсивности потоков заявок разной ширины в течение недели

 

5 Сравнение моделей

Осуществим моделирование этих моделей (табл. 1). Очевидно, что качество модели резко падает после допущения, сделанного в модели ~$HΓ/$HΓ^/1024, поэтому оно нецелесообразно.

В плане близости к результату наиболее хорошей является модель $HΓ/$HΓ^/1024. К тому же, она не требует хранения больших объемов данных (не нужно хранить информацию об изменениях интенсивности или интенсивностей в течение недели). 

Таблица 1 — Модели для LANL CM5

 

ЗАКЛЮЧЕНИЕ

Таким образом, был проведен анализ уже существующих стохастических моделей и были предложены свои модели вычислительного кластера. Стоит отметить, что полученные здесь результаты не являются панацеей, то есть для другого кластера самой хорошей может получиться совсем другая модель.

Библиографический список:

1. Интернет-портал по грид-технологиям :: GRIDCLUB.RU [Электронный ресурс]. – [2011]. – Режим доступа : http://gridclub.ru/
2. Проблемы моделирования GRID-систем и их реализация [Электронный ресурс] / О. И. Самоваров [и др.] // Портал «Информационно-коммуникационные технологии в образовании». – [2010]. – Режим доступа : http://www.ict.edu.ru/vconf/files/9451.pdf
3. Kendall's notation [Электронный ресурс] // Wikipedia. – [2013]. – Режим доступа : http://en.wikipedia.org/wiki/Kendall%27s_notation
4. Гаевой, С.В. Аппроксимация стохастических параметров вычислительного кластера на примере LANL CM5 / Гаевой С.В., Аль-Хадша Ф.А.Х. // Perspektywiczne opracowania sa nauka i technikami – 2013 : mater. IX miedzynarod. nauk.-prakt. konf., 7–15 listopada 2013 r. Vol. 33. Matematyka. – Przemysl, 2013. – S. 67–70.
5. Logs of Real Parallel Workloads from Production Systems [Электронный ресурс] // The Rachel and Selim Benin School of Computer Science and Engineering. – [2013]. – Режим доступа : http://www.cs.huji.ac.il/labs/parallel/workload/logs.html
6. Фоменков, С. А. Моделирование систем [Электронный ресурс] / С. А. Фоменков. – Волгоград, [2004]. – 1CD-ROM
7. Шеннон, Р. Имитационное моделирование систем – искусство и наука / Р. Шеннон ; пер. с англ. под ред. Е. К. Масловского. – М. : Мир, 1978. – [418 c.]
8. Логическая схема имитационной модели [Электронный ресурс] // Моделирование систем. – [2013]. – Режим доступа : http://sardismusic.com/t3r4part1.html
9. Системы массового обслуживания [Электронный ресурс] // КузГТУ / Кафедра ПИТ. – [2013]. – Режим доступа : http://vtit.kuzstu.ru/stat/template/enterprises/e8description.htm
10. Joefon Jann, Pratap Pattnaik, Hubertus Franke, Fang Wang, Joseph Skovira, and Joseph Riodan, Modeling of Workload in MPPs''. In Job Scheduling Strategies for Parallel Processing, D. G. Feitelson and L. Rudolph (Eds.), Springer-Verlag, 1997, Lect. Notes Comput. Sci. vol. 1291, pp. 95-116.
11. H. Franke, J. Jann, J. E. Moreira, P. Pattnaik, and M. A. Jette, An Evaluation of Parallel Job Scheduling for ASCI Blue-Pacific''. In Supercomputing '99, Nov 1999.
12. The Jann et al 1997 Model [Электронный ресурс] // The Rachel and Selim Benin School of Computer Science and Engineering. – [2013]. – Режим доступа : http://www.cs.huji.ac.il/labs/parallel/workload/m_jann97/
13. Maria Calzarossa and Giuseppe Serazzi, A Characterization of the Variation in Time of Workload Arrival Patterns''. IEEE Trans. Comput. C-34(2), pp. 156-162, Feb 1985.
14. The Calzarossa & Serrazi 1985 Model [Электронный ресурс] // The Rachel and Selim Benin School of Computer Science and Engineering. – [2013]. – Режим доступа : http://www.cs.huji.ac.il/labs/parallel/workload/m_calzarossa85/
15. Uri Lublin and Dror G. Feitelson, The Workload on Parallel Supercomputers: Modeling the Characteristics of Rigid Jobs. J. Parallel & Distributed Comput. 63(11), pp. 1105-1122, Nov 2003.
16. Lublin, 1999 [Электронный ресурс] // The Rachel and Selim Benin School of Computer Science and Engineering. – [2013]. – Режим доступа : http://www.cs.huji.ac.il/labs/parallel/workload/models.html#lublin99