Нахождение кратчайших путей на графе. Алгоритм Флойда. Распараллеливание алгоритма.

Автор: Стретович А.В.
Источник: Тезизы доклада, подготовленного в рамках курса «Параллельные информационные системы»

Алгоритм Флойда.

Математические модели в виде графов широко используются при моделировании разнообразных явлений, процессов и систем. Как результат, многие теоретические и реальные прикладные задачи могут быть решены при помощи тех или иных процедур анализа графовых моделей. Среди множества этих процедур может быть выделен некоторый определенный набор типовых задач на графах. Одной из таких задач является поиск минимального пути от одной вершины до другой.

Под графом G понимается упорядоченная пара (V,E), где V-множество вершин, а E-множество пар вершин (ребра). В графе каждому ребру может быть приписана некоторая характеристика, выражаемая неотрицательным числом, - вес ребра. Граф в общем случае будем считать ориентированным.

Мы используем представление графа в виде матрицы смежностей.

Алгоритм очень прост — сначала происходит инициализация матрицы кратчайших расстояний D⁰, изначально она совпадает с матрицей смежности, в цикле увеличиваем значение k и пересчитываем матрицу расстояний, из D⁰ получаем D¹, из D¹ — D² и так далее до k=n.

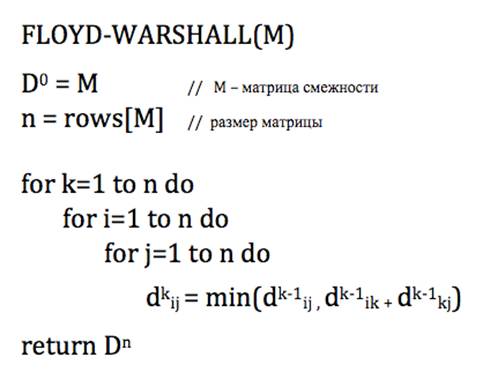
Рисунок 1 – Алгоритм Флойда

Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно[1].

Разделение вычислений на независимые части

Как следует из общей схемы алгоритма Флойда, основная вычислительная нагрузка при решении задачи поиска кратчайших путей состоит в выполнении операции выбора минимальных значений. Данная операция является достаточно простой, и ее распараллеливание не приведет к заметному ускорению вычислений.

Более эффективный способ организации параллельных вычислений может состоять в одновременном выполнении нескольких операций обновления значений матрицы A

Выполнение вычислений в подзадачах становится возможным только тогда, когда каждая подзадача (i, j) содержит необходимые для расчетов элементы A_ij, A_ik, A_kj матрицы A. Для исключения дублирования данных разместим в подзадаче (i, j) единственный элемент A_ij, тогда получение всех остальных необходимых значений может быть обеспечено только при помощи передачи данных.

Таким образом, каждый элемент A_kj строки k матрицы A должен быть передан всем подзадачам (k, j), 1<=j<=n. Такая операция может быть выполнена за log₂p шагов. С учетом количества итераций алгоритма Флойда при использовании модели Хокни общая длительность выполнения коммуникационных операций может быть определена при помощи следующего выражения

$T_p(comm)=n\lceil\log_2p\rceil(\alpha+wn/ \beta),$

где, как и ранее, α– латентность сети передачи данных, β– пропускная способность сети, а ω - есть размер элемента матрицы в байтах.

Как правило, число доступных процессоров p существенно меньше, чем число базовых задач n² (p<<n²).

Возможный способ укрупнения вычислений состоит в использовании ленточной схемы разбиения матрицы A – такой подход соответствует объединению в рамках одной базовой подзадачи вычислений, связанных с обновлением элементов одной или нескольких строк (горизонтальное разбиение) или столбцов (вертикальное разбиение) матрицы A. Эти два типа разбиения практически равноправны – учитывая дополнительный момент, что для алгоритмического языка C массивы располагаются по строкам, будем рассматривать далее только разбиение матрицы A на горизонтальные полосы.

Следует отметить, что при таком способе разбиения данных на каждой итерации алгоритма Флойда потребуется передавать между подзадачами только элементы одной из строк матрицы A. Для оптимального выполнения подобной коммуникационной операции топология сети должна обеспечивать эффективное представление структуры сети передачи данных в виде гиперкуба или полного графа[2].

Рисунок 2 – Схема разбиения по строкам [3]

Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы А. Всего в подзадачах n²/p таких элементов, число итераций алгоритма равно n.

С учетом полученных соотношений общее время выполнения параллельного алгоритма Флойда может быть определено следующим образом: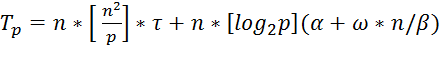

Здесь τ есть время выполнения операции выбора минимального значения.

Альтернативный подход позволяет использовать двумерное разбиение. Эта версия позволяет использовать до N²процессоров.

Рисунок 3 – Схема разбиения по строкам и столбцам [3]

На к-том шаге элементам из блока помимо собственных локальных данных понадобится информация из к-той строки и к-ого столбца.

На каждом из N шагов N/√P значений должно быть передано √P подзадачам в каждом столбце и строке. Общая стоимость в таком случае:

Рисунок 4 – Время работы альтернативного метода

Такой подход намного сложнее в реализации, но работает быстрее за счет уменьшения размера передаваемых данных.

Результаты вычислительных экспериментов

Показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид:

Следовательно, общий анализ сложности дает идеальные показатели эффективности параллельных вычислений[2].

Приведем также данные экспериментов университета г. Манитоба. Материалы взяты из презентации студента Inderjeet Singh [4]

На рисунке 5 показано, что существует значительный разрыв в показателях времени выполнения для матрицы размером 2048*2048 при увеличении количества процессоров. После 80 процессоров время выполнения почти не изменяется.

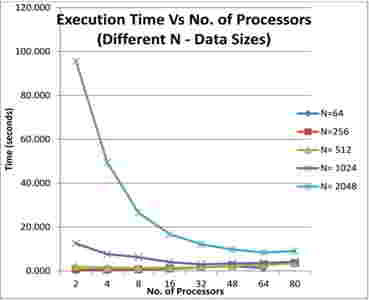
Рисунок 5 – Показатели зависимости времени от числа процессоров

Для матрицы размером 256 происходит увеличение времени выполнения при добавлении процессоров. Это можно объяснить тем, что для малых размеров матрицы время передачи сообщений перевешивает время вычислений.

Данные для обработки становятся более фрагментированными при большем числе процессоров – отсюда дополнительная передача сообщений.

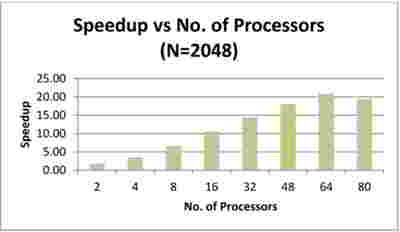
Рисунок 6 – Показатели ускорения

Из рисунка 7 видно, что при добавлении процессоров увеличивается ускорение, но постоянное ускорение не достигается.

Сравнивая показатели реализаций алгоритма на MPI и OpenMP, можно увидеть, что MPI лучше подходит для решения этой задачи.

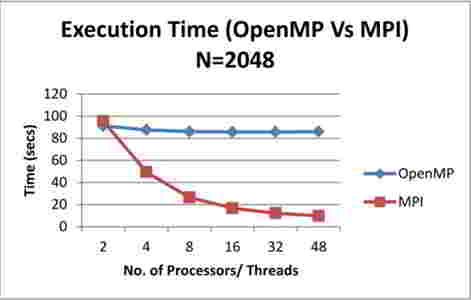
Рисунок 7 – Сравнение работы реализаций

Перечень ссылок:

1. Алгоритм Флойда - Уоршелла [Электронный ресурс] Режим доступа: http://habrahabr.ru/post/105825/

2. Теория и практика параллельных вычислений. Лекция 10: Параллельные методы на графах [Электронный ресурс] Режим доступа: http://www.intuit.ru/studies/courses/1156/190/lecture/4960%252525253Fpage%252525253D5

3. Case Study: Shortest-Path Algorithms [Электронный ресурс] Режим доступа: http://www.mcs.anl.gov/~itf/dbpp/text/node35.html#figgrfl3

4. Inderjeet Singh – All Pair Shortest Path Algorithm – Parallel Implementation and Analysis [Электронный ресурс] Режим доступа: http://www.slideshare.net/singhinderjeet/parallel-all-pair-shortest-path-algorithm