Исследование изображений Солнца представляет собой весьма актуальную задачу. Анализ таких изображений позволяет как получать новую информацию о процессах, происходящих на самом Солнце, так и исследовать солнечно‑земные связи.
Изображение Солнца представляет собой очень сложную картину с десятками появляющихся, изменяющихся и исчезающих объектов. Один из распространеных типов объектов – корональные дыры, являющиеся источником корональных выбросов массы, которые, будучи направлены в сторону Земли, при определенных условиях способны вызвать на Земле магнитные бури [4]. Задача прогнозирования геомагнитных бурь требует изучения поведения корональных дыр и других существующих на Солнце объектов.
В общей форме задача анализа изображений Солнца состоит в анализе многомерных временных рядов параметров, характеризующих поведение объектов на Солнце, с целью прогнозирования наступления определённого события (например, геомагнитной бури) в предположении, что наступлению события всякий раз предшествует явление – некая заранее неизвестная комбинация значений этих параметров. При этом важно уметь локализовать такое явление во времени с хорошей точностью. Для решения этой задачи может быть использован разрабатываемый с участием авторов настоящей работы нейросетевой алгоритм прогнозирования событий и поиска предвестников в многомерных временных рядах [3]. Однако для применения такого алгоритма необходимо существенно снизить размерность входных данных, по возможности сохраняя всю существенную для решения задачи информацию.
В настоящей работе проводится исследование возможности применения вейвлет‑анализа для предобработки изображений объектов на Солнце с целью выделения небольшого количества информативных признаков. При этом происходит понижение размерности анализируемой информации, в контексте выявления качественных изменений пространственных свойств объектов на изображении Солнца.
Анализируемые объекты извлекаются из изображений Солнца, полученных со спутника SOHO – совместного проекта Европейского Космического Агентства (ESA) и NASA (http://sohowww.nascom.nasa.gov/).
Установленные на спутнике приборы позволяют определять распределение плазмы в солнечной короне на разных высотах за счет исследования изображения Солнца в различных спектральных линиях (приборы EIT – Extreme Ultraviolet Imaging Telescope), измерять магнитные поля (на основе эффекта Зеемана), поля скоростей на поверхности (прибор MDI/SOI – Michelson‑Doppler Imager/Solar Oscillations Investigation) и др.
Объекты, которые необходимо описать с помощью небольшого набора признаков, имеют сложную произвольную форму. Кроме того, они постоянно эволюционируют. Помимо этого, вращение Солнца также вносит деформации в изображение объекта. Для решения поставленной задачи необходимо выделить такие признаки, которые будут устойчивы по отношению к постоянно происходящим деформациям объекта, но при этом смогут хорошо выявлять качественные изменения его пространственных свойств. Для решения этой задачи предлагается использовать вейвлет‑преобразование [1, 5]. Суть предлагаемой методики заключается в следующем. Мы предполагаем, что при непрерывно происходящей эволюции объекта энергия вейвлет‑коэффициентов, соответствующих определенному масштабу, сохраняется. Но когда происходит явление, способное вызвать событие, происходит качественное изменение пространственных свойств объекта, и энергия вейвлет‑коэффициентов начинает перераспределяться между различными уровнями детализации.
Пусть wij – j‑ый вейвлет‑коэффициент, соответствующий i‑му уровню детализации. Энергия, заключенная в нем, равна. Мы используем ортонормированный базис Coiflet6, поэтому суммарная энергия коэффициентов разложения равна суммарной энергии исходного изображения. Энергия на определенном уровне детализации – это сумма энергий вейвлет‑коэффициентов, соответствующих этому уровню:
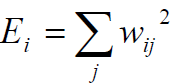 , ,
|
(1) |
В качестве признаков мы используем доли энергии, сосредоточенной в вейвлет‑коэффициентах определенного масштаба, т. е.:
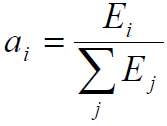 , ,
|
(2) |
Анализируются изображения 128×128 точек, декомпозиция производится до 6‑го уровня, поэтому количество масштабов равно 6. Сглаживающие коэффициенты, соответствующие усреднению изображения, в данной работе не используются, т. к. они имеют другую нормировку (имеют масштаб яркости объекта, а не масштаб её изменений, и потому не могут использоваться в нормировке коэффициентов на сумму). Соответственно, из каждого изображения выделяются 6 признаков, которые описывают его пространственные свойства. Подчеркнём, что, наряду с энергиями вейвлет‑коэффициентов, в качестве формируемых признаков могут использоваться и другие признаки самой разной природы, однако сравнительный анализ результатов использования различных способов формирования признаков лежит за рамками настоящей работы.
Для проверки выдвинутого предположения об устойчивости нашего метода к различным преобразованиям объекта были проведены эксперименты с модельными объектами. Для экспериментов была выбрана двумерная кривая Гаусса (далее – "двумерный гауссиан") как наиболее простая модель локализованного объекта. Двумерный гауссиан подвергался преобразованиям масштабирования по одной и обеим координатам; полученный “гауссиан” с разными характерными размерами в перпендикулярных направлениях подвергался также преобразованиям вращения. Для моделирования “расходящейся волны” использовался тороподобный объект, полученный вращением вокруг оси гауссиана с центром, находящимся на фиксированном расстоянии от оси вращения (превышающем характерный размер самого гауссиана). Проведенные эксперименты показали устойчивость набора признаков по отношению к вышеприведенным преобразованиям [2].
Также были проведены эксперименты с реальными изображениями солнечных объектов. Объекты на Солнце имеют сложную 3‑мерную пространственную структуру. В то же время, изображения, получаемые с помощью телескопа, представляют собой проекции 3‑мерных объектов на плоскость, и не дают представления об объемном распределении плазмы. Для исследования плазмы на различных высотах можно регистрировать изображения Солнца в разных спектральных линиях, то есть выделять излучение, характерное для определенной температуры, и, следовательно, высоты соответствующего слоя. Ультрафиолетовый телескоп EIT спутника SOHO позволяет получать изображения Солнца в четырех спектральных линиях:
1) 171 A (Fe IX‑X), температура плазмы 1.3 MK.
2) 195 A (Fe XII), температура плазмы 1.6 MK.
3) 284 A (Fe XV), температура плазмы 2 MK.
4) 304 A (He II), температура плазмы 5‑8 KK.
На рис. 1 и рис. 3 приведены изображения в линии 195 A и распределение магнитного поля на поверхности Солнца. На рис. 1 показан объект, с которым происходят качественные изменения, на рис. 3 представлен стационарный объект. Соответствующие изменения вейвлет‑признаков показаны на рис. 2 и рис. 4.

Рисунок 1 – Возникновение и эволюция объекта. Вверху – изображение активной области в линии 195 A, внизу – её изображение, полученное из магнитограммы.
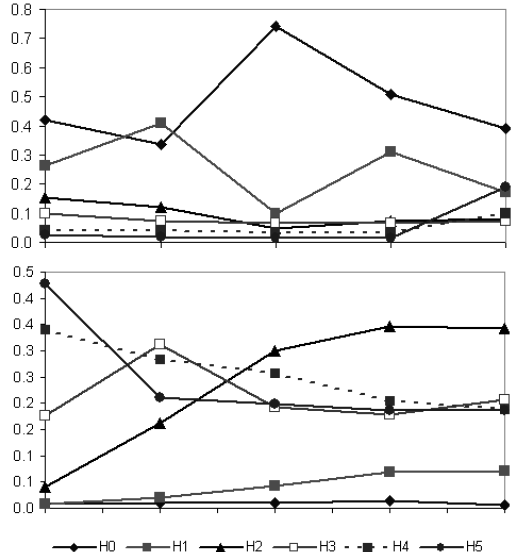
Рисунок 2 – Графики значений вейвлет‑признаков, соответствующих изображениям объекта на рис. 1. Вверху – признаки, соответствующие изображению объекта в линии 195 A, внизу – признаки, соответствующие изображению объекта, полученному из магнитограммы.

Рисунок 3 – Изображения объекта, полученные через равные промежутки времени. Вверху – изображение акивной области в линии 195 A, внизу – ее изображение, полученное из магнитограммы.
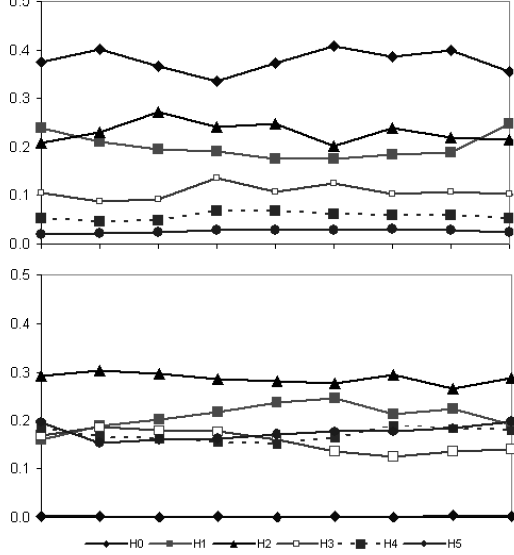
Рисунок 4 – Динамика вейвлет‑признаков, сформированных из последовательности изображений объекта, приведенной на рис. 3. Вверху – признаки, соответствующие изображению объекта в линии 195 A, внизу – признаки, соответствующие изображению объекта, полученному из магнитограммы.
Анализ динамики вейвлет‑признаков для этих и других исследованных объектов позволяет утверждать, что:
1) Вейвлет‑признаки стационарных объектов изменяются сравнительно слабо по сравнению с признаками качественно изменяющихся объектов.
2) Характер изменения вейвлет‑признаков нестационарных объектов отражает динамику изменения их пространственных свойств.
Полученные результаты дают все основания предполагать, что вышеописанный алгоритм выделения признаков на основе вейвлет‑преобразования может быть успешно применен для выделения информативных признаков изображений объектов на Солнце. Критерием того, насколько в действительности информативными окажутся выделяемые таким способом признаки, могут служить только результаты применения предложенных признаков для решения практической задачи, например, задачи прогнозирования геомагнитных бурь. В дальнейшем планируется использовать описанные в настоящей работе вейвлет‑признаки для предобработки входных данных при решении задачи прогнозирования геомагнитных бурь с помощью нейросетевого алгоритма [3].
Работа выполнялась при частичной финансовой поддержке Министерства промышленности, науки и технологий РФ, Госконтракт № 37.011.1.0016 от 01.02.2002, доп. соглашение № 4 от 18.03.2004.
- И. М. Дремин, О. В. Иванов, В. А. Нечитайло. Вейвлеты и их использование. Успехи физических наук, Май 2001 г., Том 171, № 5, стр. 465.
- С. А. Шаров. Применение вейвлет‑преобразования для компрессии и анализа изображений в физическом эксперименте. Дипл. раб., физический ф‑т МГУ им. М. В. Ломоносова, М., 2004.
- S. A. Dolenko, Yu. V. Orlov, I. G. Persiantsev, Ju. S. Shugai. A search for correlations in time series by using neural networks. Pattern Recognition and Image Analysis, 2003, v.13, No. 3, pp.441–446.
- Journal of the Communications Research Laboratory, 2002, v.49, No. 3,4 (Special Issue on Space Weather Forecast 1,2).
- G. Strang, T. Nguyen. Wavelets and Filter Banks. Wellesley‑Cambridge Press, 1996.