Многокритериальная оптимизация времени, стоимости, качества с использованием мультиколониального муравьиного алгоритма
Авторы: A. Afshar, A. Kaveh and O.R. Shoghli
Автор перевода: К.Б. Зуй
Источник: Asian Journal of Civil Engineering (Building and Housing) Vol. 8, No. 2 (2007) pages 113-124
Аннотация
A. Afshar, A. Kaveh and O.R. Shoghli Многокритериальная оптимизация времени, стоимости, качества с использованием мультиколониального муравьиного алгоритма. Строительные планировщики часто сталкиваются с проблемой оптимального использования ресурсов, чтобы найти компромисс между различными и обычно конфликтующими аспектами проектов. Время, стоимость и качество реализации проекта являются одними из важнейших аспектов каждого проекта. Появление новых видов договоров, которые требуют максимизации качества проектов и одновременно минимизации его временных и финансовых затрат, требует разработки обширных моделей, которые учитывают качество в сумме с временем и затратами. В этой статье разрабатывается новый метаэвристический мультиколониальный муравьиный алгоритм для оптимизации трех параметров (времени, стоимости, качества), использую компромиссный подход. Рассмотрен пример, чтобы проиллюстрировать возможности существующего метода в нахождении оптимальных (около оптимальных) решений. Также модель применяется для проблемы поиска компромисса между временем и стоимостью, результаты сравниваются с результатами, полученными с помощью существующих методов.
Введение
Традиционная проблема компромисса между временем и стоимостью была предметом интенсивных исследований с времен появления Метода критического пути (CPM) в конце 1950-х. Строительные планировщики часто сталкиваются с проблемой оптимального использования ресурсов, чтобы найти компромисс между различными и обычно конфликтующими аспектами проектов, особенно времени и затрат. Недавно появившиеся виды контрактов учитывают качество исполнения проектов в сумме с временем их выполнения и затратами на проекты. Эти контракты оказали давление на лиц, принимающих решения в строительной отрасли для поиска оптимального / почти оптимального плана использования ресурсов, чтобы минимизировать стоимость и время строительства при максимальном качестве. Это создает новую и настоятельную необходимость в современных моделях использования ресурсов, которые способны оптимизировать многочисленные и противоречивые параметры строительства: время, стоимость и качество. El-Rayes и др. [1].
Если длительность деятельности (работы, операции) уменьшается, то стоимость будет увеличиваться за счет дополнительных ресурсов, выделяемых для ускоренного выполнения. С другой стороны, использование меньшего количества ресурсов приведет к увеличению продолжительности деятельностей. Каждый вариант использования ресурсов (время и стоимость в совокупности) даст определенное качество работы. Нахождение компромисса между этими конфликтующими аспектами проекта – сложная задача. Планировщики сталкиваются с многочисленными возможными комбинациями для реализации проекта. Например, число возможных комбинаций выполнения проекта с 18 деятельностями и 4 возможными вариантами использования ресурсов для каждого вида деятельности будет более 6 млрд. Разрабатываемый алгоритм может быть стоящим комплексным эффективным инструментом поиска компромисса между временем, затратами и качеством.
Для решение проблемы компромисса между временем и стоимостью было использовано множество методов. Существующие модели можно разделить на эвристические и методы математического программирования. (Feng и др. [2]). Учитывая количество параметров модели, эти методы могут быть разделены на категории, как показано в таблице 1. Недостатки этих методов подробно описаны в следующей литературе (например, Zheng и др. [3]), но главным их недостатков является невозможность учитывать больше одного параметра. К тому же, эти методы обычно используют алгоритмы поднятия на вершину, которые предполагают случайную генерацию только одного решение, которое подвергается изменению, чтобы получить решение лучше данного.
| Минимизация времени проекта и/или оптимизация использования ресурсов | Компромисс между временем и стоимостью для однократного строительства | Минимизация времени и/или стоимости для многократного строительства | Минимизация времени и/или стоимости и максимизация качества |
|---|---|---|---|
| Burns et al. 1996 | |||
| Feng et al. 1997 | El-Rayes and Moselhi 2001 | Bubu and Suresh 1996 | |
| Easa 1989 | Li and Love 1997 | Khang an Myint 1999 | |
| Chan et al. 1996 | Maxwell et al. 1998 | Hegazy and Ersahin 2001 | El-Rayes and Kandil 2005 |
| Hegazy 1999 | Li et al. 1999 | Hegazy and Wassef 2001 | |
| Gomar et al. 2002 | Feng et al. 2000 | Leu and Hwang 2001 | |
| Zheng 2004 | |||
| Zheng et al 2005 |
Проблема нахождения компромисса между временем, стоимостью и качество до 2005 года была поднята только в работах Bubu et al. [4] и затем Khang et al. [5]. В 2005 El-Rayes и др. [1] доложили о своих исследованиях в этой области. Был использован многокритериальный генетический алгоритм. В этой статье для решения поставленной задачи применяется новый метаэвристический подход, основанный на мультиколониальном муравьином алгоритме.
Муравьиный алгоритм для мультикритериальной оптимизации
В этом разделе представлен муравьиный алгоритм для мультикритериальной оптимизации.
Муравьиный алгоритм
В последние годы эволюционные и метаэвристические алгоритмы активно использовались как инструмент оптимизации в различных сферах, таких как наука, коммерция, инженерия. Простота использования, широкое распространение и большие перспективы предопределили их успех. Муравьиный алгоритм (МА) вдохновляет тем фактом, что муравьи могут находить кратчайший путь от своего гнезда до источника пищи, не смотря на то, что они почти слепы (Dorigo и др. [6]). В ходе исследований было установлено, что муравьиный алгоритм обладает прочностью
и мощностью для нахождения оптимальных/почти оптимальных решений в особенности дискретных задач.
В общем виде, МА применяет конечное множество искусственных муравьев с определенными характеристиками, которые коллективно находят качественное решение рассматриваемой задачи. Начиная с шага инициализации, выбранный по определенному критерию, каждый муравей строит решение похожее на хромосому в генетическом алгоритме. Строя свое решение, каждый муравей собирает информацию сам и использует ее, чтобы представление проблемы, которое представили другие муравьи (Dorigo и др.[6]).
Внутренние состояния муравья хранят информации о прошлом поведении муравья, которое может быть использован для вычисления фитнесфункции генерируемого решения. Искусственному муравью разрешается изменить уровень феромонов при разработке решения или построение полного решения, или оба этих варианта. Количество феромонов выполнен пропорционально оптимальности найденного решения, которое искусственный муравей разработал (или разрабатывает).
Быстрое дрейф всех муравьев по одному и тому же участку можно избежать, используя определенный способ выбора перехода муравьев и механизма испарения феромонов. Для того чтобы имитировать испарение феромонов, вводиться коэффициент интенсивности испарения феромонов (p), что позволяет более глубоко изучить пространство поиска и сводит к минимуму вероятность преждевременной сходимости к субоптимальным решений. Также используется вероятностный подход выбору перехода для муравьев, чтобы изменить направление их поиска в наиболее интересные регионов пространства поиска. Уровень стохастичности в политике выбора перехода и интенсивность обновления феромона определяет баланс между разведыванием новых точек пространства и эксплуатацией накопленных знаний (Dorigo и др. [6]).
Пусть τij(t) – общий уровень феромонов, отложенный на пути ij в момент времени t, а ηij(t) – эвристическая стоимость пути ij в момент времени t в соответствии с целевой функции. Вероятность перехода от узла i к узлу j в момент времени Т может быть определен как (Dorigo и др. [7].):
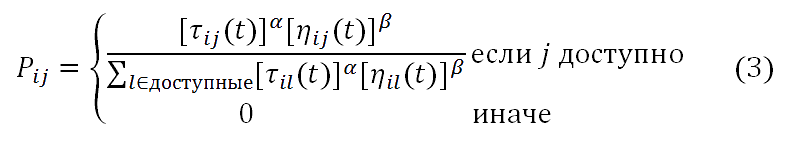
где α и β являются параметрами, которые контролируют относительную важность феромона след по сравнению с эвристическим расстоянием. Пусть q случайная величина, равномерно распределены по [0, 1], и q0 ∈ [0, 1] настраиваемый параметр. На следующий узел j, который муравей выбирает для перехода (Dorigo и др.[6]):.
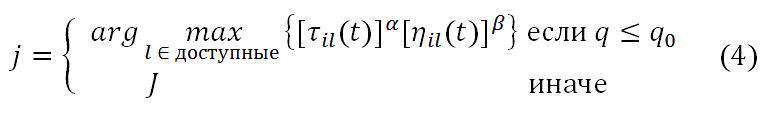
Где J - случайная величина выбранная в соответствии с распределением вероятностей pij(t). Уровень феромонов изменяется глобально. По окончанию прохождения всех муравьев в колонии, происходит обновление феромонов следующим образом:
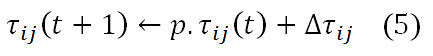
Где 0≤p≤1; p - коэффициент испарения, символ ← используется, чтобы показать следующую итерацию и Δt обозначает значение обновления
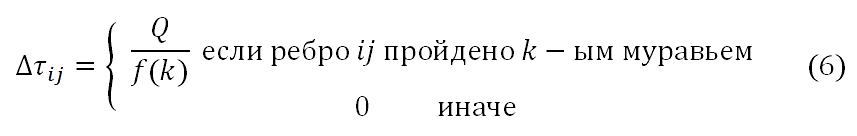
где Q является константой, представляющей количество феромонов, отложенной муравьем и f(k) является значением целевой функции на каждой итерации.
Многоцелевая оптимизация
Многие проблемы реальной жизни являются оптимизацией функции более, чем с одним критерием. Фактически оптимизации по нескольким критериям привела к проблеме решения более сложной многоцелевой оптимизации. Существование множества многокритериальных проблем в реальном мире, их внутренней сложности и преимущества метаэвристических процедуры, спровоцировали исследование этой области в последние несколько лет (Gandiblex и др. [8];. Голдберг [9]).
Некоторые исследователи использовали генетические алгоритмы для решение задачи компромисса между временем и стоимостью, но не было представлено метода, использующего МА для решение данной задачи.
Фронт Парето
Как уже упоминалось целью многокритериальной оптимизации является нахождение лучшего компромисса между конфликтующими критериями. Учитывая все критерии задач, находятся более чем одно решение, но не одно из них не является явно оптимальней других. Обычно существует более, чем одно решение, которое лучше остальных и учитывает все критерии.
Поэтому мы сталкиваемся с множеством решений, которые лучше, чем остальные и называются фронтом Парето. Среди возможных решений решения, относящиеся к фронту Парето, известны как недоминирующие решения в то время, как остальные решения – доминирующие. Поскольку не одно решения из фронта Парето не может быть абсолютно лучше других, все они одинако предпочтительны для удовлетворения всех критериев.
Описание проблемы и разработки
В рассматриваемой задаче каждая деятельность имеет варианты для оптимизации распределения ресурсов и наша цель состоит в нахождении оптимальных/почти оптимальных решений проекта в поле всех возможных решений. Для применения МА к решению проблемы она должна быть представлена в виде графа и схожей по структуре модели для прохождения по ней муравьев, что и показано на рисунке 1. На нем представлен проект из N деятельностей и K критерием оптимальности. Горизонтальная ось представляет собой деятельности, а вертикальная – критерии. Стрелками обозначен путь, который является типичным решением, которое может быть выбрано муравьем. Для большей наглядности и возможности ссылаться задан вектор для каждго возможного решения, которое демонстрирует вариант распределения ресурсов для каждой деятельности. Например, для пути, показанном на рисунке 1 вектор будет иметь следующий вид: V = [2, 3, 1, k, k, ..., 3].
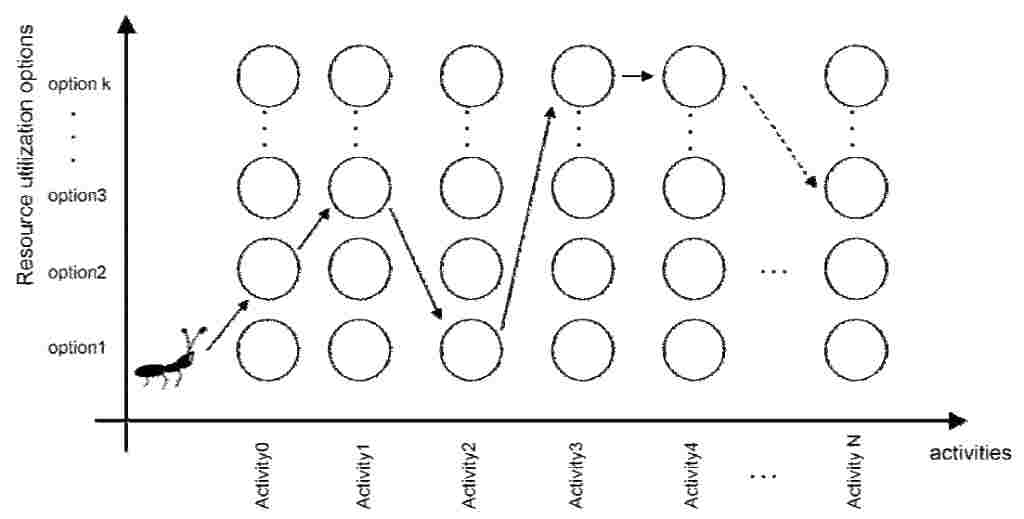
Рисунок 1 – График представление задачи для проекта с деятельностями N и K ресурсами
Проблема в основном состоит в выборе соответствующего варианта для каждой деятельности для получения времени, стоимости и качества проекта. Критерий времени может быть выражен как
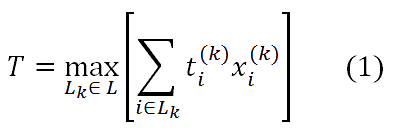
где ti(k) – длительность деятельности i, которая выполняется по варианту k xi(k) – индекс переменной деятельности, который равен 1, если деятельность выполняется по варианту k и 0, если не выполняется. Сумма индексов переменных для каждого варианта должна равняться 1. Lk означает последовательность деятельностей на k-ом пути и Lk={i1k, i2k, …, ink} где ijk представляет собой последовательность номером деятельности j на пути k. L служит для множества путей графа и L={Lk|k=1,2,…,m}, где m означает количество путей в графе. Другими словами, для каждой комбинации с помощью выще упомянутой формулы будет рассчитываться сумма длительностей на критическом пути графа проекта.
Общая стоимость проекта состоит из двух частей: прямых расходов и косвенных затрат. Прямые затраты определяется как сумма стоимостей на все виды деятельности в рамках проекта. С другой стороны, косвенные расходы состоит из расходов по управлению проектом, которые в значительной степени зависят от продолжительности проекта, то есть, чем дольше длится проект, тем выше косвенные расходы.
В реальном строительном проекте, целесообразно оценить косвенные затраты за единицу времени, чтобы рассчитать общую стоимости. Впоследствии уравнение (2) может быть применено для вычисления общей стоимости проекта:
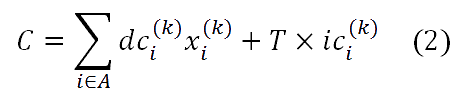
где dci(k) – прямая стоимость деятельности i в варианте k, которая равна качеству работы умноженной на цен; ici(k) – косвенная стоимость деятельности за единицу времени в варианте k, которая может быть установлена оценками экспертов или производной от деления косвенной стоимости на бюджет; A – множество деятельностей.
Представление качества строительства в виде функции от разных ресурсов – это сложная задача из-за трудностей измерения влияния этих стратегий на проведения работ на их качество. Кроме того, это сложная работа оценить долю отдельного качества исполнения деятельности на общий уровень качества проекта. Некоторые показатели были изучены и определены в последних исследованиях, которые были направлены на развитие качества на основе подрядных предквалификационных системы (Anderson и Russell [10]; Минчин и Смит [11]). Идентифицированные качественные показатели были получены из моделей, основанных на производительности, которые коррелируют долгосрочную производительность конечного продукта каждый вид деятельности на его качественные показатели. Критерием качества может служить следующая функция:
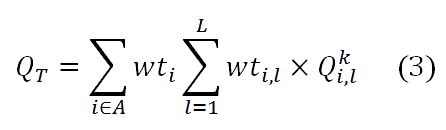
где Qi,lk – представление индикатора качества (l) в деятельности (i) с помощью использования ресурсов (k); wti,l - вес показателя качества (l) по сравнению с другими видами деятельности в проекте (Эль-Rayes [1]). Общее качество на уровне проекта вычисляется по формуле (3).
Предложенный мультиrолониальный муравьиный алгоритм для нахождения компромисса между временем, стоимостью и качеством
В предложенном не доминирующем архивном МА алгоритме, для каждого параметра назначается колония агентов. Все колонии имеют одинаковое количество муравьев. Все муравьи одной колонии пытаются найти решение соответствии с назначенным критерием.
Решения, найденные для одного критерия за один цикл, не оцениваются соответствующей колонией. Полученные решения переносятся на следующую колонию и должны быть оценены в соответствии с назначенным критерием, тогда глобальной след этой колонии обновляется. Новые решения, найденные на основе нового следа феромонов во втором колонии, передаются третьей колоний. Этот процесс (нахождения множества решений и использование этих решений для обновления) продолжается до заранее определенной итерации называемой итерацией цикла. На этом этапе, значения критериев рассчитываются в соответствии с сгенерированными решениями третьей колонии и недоминирующие решения перемещаются во внешнее множество называемое архивом. После завершения цикла, глобальный следы феромона всех колоний установливается в начальное значение τ0. На следующем этапе, второй цикл начинается и в конце цикла, полученные недоминирующие решения перемещаются в том же архив. Доминирующие решения архива отбрасываются и происходит обновление уровня феромонов согласно существующим решениям в архиве. Весь процесс повторяется, пока все недоминирующие решения (множество Парето) архива удовлетворяют всем ограничениям или заранее определенное число итераций выполняется. Решения архива – окончательное решение Парето для проблемы многокритериальной оптимизации. Для достижения лучшего распределения решений Парето, на каждом шаге все произведенные решения оцениваются в соответствии с тремя критериями и недоминирующие решения перемещаются в архив. Если есть решение, которое доминирует, они будут удалены.
Пример
Для того чтобы проиллюстрировать концепцию и производительность предложенного алгоритма, используется тестовый проект с подробной информацией, что показано в таблице 2. Пример был первоначально введена Feng и др. [12], а затем то же использоваться Zheng и др. [13] для анализа компромисса времени и стоимости в строительстве. Таблица 2 включает в себя данные о распределении ресурсов и их время, стоимость и качество. Косвенные расходы равны 500$/день. Первоначально пример не содержат информацию об уровне качества вариантов использования ресурсов. При этом они представлены на основе качественных индикаторов и упомянутых процедур. Результаты, сообщенные Zheng [13] для многокритериального подход с адаптацией весов (MAWA), используются для проверки результатов, предусмотренных действующим подходом.
Предлагаемый мультиколониальный муравьиный алгоритм был применен к данным проекта, которые показаны в таблице 2.Количество муравьев в каждой колонии, количество циклов итераций и общее число итераций равны 50, 20 и 60, соответственно. Другие параметры алгоритма равны p= 0,97, α = 2, β = 0, а параметр Q для колоний времени, стоимости и качества равен 10, 10000, 0.0005.
| Деятельность | Предшествующая деятельность | Вариант ресурсов | Длительность (дни) | Стоимость ($) | Вес деятельности (%) | Качество (%) |
|---|---|---|---|---|---|---|
| 1 | 1 2 3 |
14 20 24 |
23,000 18,000 12,000 |
8 | 98 89 84 |
|
| 2 | 1 | 1 2 3 4 5 |
15 18 20 30 60 |
3,000 2,400 1,800 1,200 600 |
6 | 99 95 85 70 59 |
| 3 | 1 | 1 2 3 |
15 22 33 |
4,500 4,000 3,200 |
14 | 98 81 63 |
| 4 | 1 | 1 2 3 |
12 16 20 |
45,000 35,000 30,000 |
19 | 94 76 64 |
| 5 | 2, 3 | 1 2 3 4 |
22 24 28 30 |
20,000 17,000 15,000 10,000 |
17 | 99 89 72 61 |
| 6 | 4 | 1 2 3 |
14 18 24 |
40,000 32,000 18,000 |
19 | 100 79 68 |
| 7 | 5, 6 | 1 2 3 |
9 15 18 |
30,000 24,000 22,000 |
17 | 93 71 67 |
Запуск модели с помощью упомянутых данных привел к выбору 103 недоминирующих решений (Парето оптимальных). Каждое решение содержит определенный оптимальный способ выполнения проекта. Множество решений обеспечивает оптимальное компромисс между времени, стоимости и качества. Образец выбранных решений показан в таблице 3.
| Решение | Время (дни) | Стоимость ($) | Качество (%) | Вариант ресурсов для деятельности | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| 1 | 60 | 155,500 | 92 | 1 | 1 | 1 | 2 | 1 | 1 | 1 |
| 2 | 61 | 142,500 | 86 | 1 | 1 | 1 | 3 | 1 | 2 | 1 |
| 3 | 62 | 163,000 | 95 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
| 4 | 63 | 131,500 | 84 | 1 | 1 | 1 | 2 | 2 | 3 | 1 |
| 5 | 65 | 162,400 | 95 | 1 | 2 | 1 | 1 | 2 | 1 | 1 |
| 6 | 66 | 128,500 | 82 | 1 | 1 | 1 | 2 | 3 | 3 | 1 |
| 7 | 67 | 127,300 | 83 | 1 | 3 | 1 | 3 | 1 | 3 | 1 |
| 8 | 68 | 118,500 | 77 | 1 | 1 | 1 | 3 | 4 | 3 | 1 |
| 9 | 71 | 117,900 | 77 | 1 | 2 | 1 | 3 | 4 | 3 | 1 |
| 10 | 74 | 112,500 | 73 | 1 | 1 | 1 | 3 | 4 | 3 | 2 |
| 11 | 78 | 107,500 | 76 | 3 | 1 | 1 | 3 | 4 | 3 | 1 |
| 12 | 87 | 150,200 | 93 | 3 | 4 | 1 | 1 | 2 | 1 | 1 |
| 13 | 92 | 98,300 | 70 | 3 | 3 | 1 | 3 | 4 | 3 | 3 |
| 14 | 126 | 104,600 | 73 | 3 | 5 | 1 | 3 | 2 | 3 | 3 |
| 15 | 132 | 95,800 | 63 | 3 | 5 | 3 | 3 | 4 | 3 | 3 |
Результаты данного подхода к решению компромисса между временем и стоимостью сравниваются с результатами Zheng и др. [13]. Количество муравьев в каждой колонии, количество циклов итераций и общее число итераций равны 20, 10 и 30, соответственно. Другие параметры алгоритма равны p= 0,97, α = 2, β = 0, а параметр Q для колоний времени, стоимости и качества равен 10, 10000, 0.0005. Результаты тестирования представлены в таблице 4.
| Решение | 50-MAWA | 100-MAWA | 30-MOACA | |||
|---|---|---|---|---|---|---|
| Время (дни) | Стоимость ($) | Время (дни) | Стоимость ($) | Время (дни) | Стоимость ($) | |
| 1 | 61 | 173,000 | 61 | 173,000 | 61 | 173,000 |
| 2 | 63 | 164,000 | 62 | 172,000 | 62 | 171,000 |
| 3 | 67 | 157,000 | 63 | 162,000 | 63 | 162,500 |
| 4 | 68 | 152,500 | 66 | 161,500 | 66 | 161,500 |
| 5 | 74 | 150,500 | 67 | 157,500 | 67 | 157,500 |
| 6 | 77 | 150,400 | 68 | 152,500 | 68 | 152,500 |
| 7 | 78 | 146,500 | 74 | 149,500 | 74 | 149,000 |
| 8 | 90 | 143,900 | 77 | 149,000 | 77 | 149,000 |
| 9 | 78 | 146,500 | 78 | 146,500 | ||
| 10 | 84 | 143,500 | 84 | 143,500 | ||
| 11 | 87 | 143,000 | 87 | 143,000 | ||
| 12 | 60 | 173,000 | ||||
Это сранение не только подтверждает возможность построенной модели генерировать множество недоминирующих решений, но и перечисляет еще одно недоминирующее решение из 100-MAWA решений всего лишь через 30 итераций.
Выводы
Мульти критериальная оптимизация с помощью МА разработана для анализа сложных проблем нахождения компромисса между временем, стоимостью и качеством. Модель способна находить компромисс между конфликтующими аспектами строительного проекта, минимизируя время и стоимость и максимизируя качество. Эффективность данного алгоритм подтверждена приведенным примером. Данный алгоритм был сопоставлен на примере с подходом Zheng [13] и доказал свою возможность решать подобные задачи.
Список использованной литературы
- Kaheled El-Rayes, Amr Kandil, Time-cost-quality trade-off analysis for highway construction, Journal of Construction. Engineering Management, No. 4, 131(2005) 477-485.
- Feng, C.W., Liu, L., and Burns, S.A., Stochastic construction time-cost trade-off analysis, J. Comput. Civ. Eng., No. 11, 3(2000)184–189.
- Zheng, D.X.M., Ng, T. S. T., and Kumaraswamy, M. M., Applying genetic algorithms techniques for time-cost optimization, Proc., 18th Annual Conf. ARCOM, D. Greenwood, ed., University of Northumbria, Middleborough, U.K., September 2-4, 2002, pp. 801-810.
- Babu, A.J.G., Suresh, N., Project management with time, cost and quality considerations, European J. Operations Research, (1996), 88, 320-327.
- Khang D.B. and Myint Y.M., Time, cost and quality trade-off in project management: a case study, International Journal of Project Management, 1999.
- Dorigo, M., Gambardella, L.M., Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Transctions on Evolutionary Computation, No. 1, 1(1997)53-66.
- Dorigo M., Optimization, learning and natural algorithms, Ph.D. thesis, Politecnics di Milano, Italy, 1992.
- Gandibleux, X., Sevaux, M., Sorensen, K. and T’ Kindt, V. (Eds), Metaheuristics for Multiobjective Optimization, Lecture Notes in Economics and Mathematical System 535, Springer Verlag, 2004.
- Goldberg, D.E., Richardson, J., Genetic algorithms with sharing for multimodel function optimization, Proc. Second International Conference on Genetic Algorithms (ICGA’87), Hillslade, USA, 1987, pp. 218-229.
- Anderson A., and Russell, J., Guidelines for warranty, multiparameter and best value contracting, NCHRP Rep. No. 451, National Cooperative Highway Research Program, Washington, USA, 2001.
- Minchin, R.E., and Smith G.R., Quality based performance rating of contractors for prequalification and bidding purposes. PTI 2001-25, The Pennsylvania Transportation Institute, Pennsylvania State University, 2007.
- Feng, C.W., Liu, L., and Burns, S.A., Using genetic algorithms to solve construction time-cost trade-off problems, J. Comput. Civ. Eng., No. 11, 3(1997) 184-189.
- Zheng Daisy X.M., S. Ng. Thomas, Stochastic time-cost optimization model