Из ранее изложенного следует, что в системах ЧМ с большой девиацией частоты при уменьшении отношения сигнал/шум наступает явление порога. Это явление наблюдалось экспериментально еще на заре развития частотной модуляции (например, Кросби [13] в 1937 г.) и впоследствии было предметом многочисленных исследований (например [14 – 20]). Райс [21] разработал полезную модель для дискриминатора, работающего вблизи своего порога. Его результаты по исследованию поведения системы ЧМ в пороговой области согласуются с экспериментальными данными. Подробное изложение этого анализа утомительно, поэтому мы просто укажем основную идею и приведем полученные им результаты.
Для облегчения понимания процесса предположим, что несущая немодулирована. Ее можно представить как вращающийся вектор – фазор (рис. 5.30, а). Частота сигнала есть просто скорость вращения, как показано на рис. 5.30, б. Вектор шума складывается с сигнальным вектором, как показано на рис. 5.30, в. Поскольку сигнальный вектор вращается с постоянной скоростью, можно просто отображать лишь относительное вращение результирующего вектора относительно сигнального вектора. Это показано на рис. 5.30, а. Когда вектор шума мал (т. е. выполняются условия (150) и (151), как показано на рис. 5.30, д), он вызывает незначительные флуктуации мгновенной частоты, как показано на рис. 5.30, е. Если вектор шума велик, то результирующий вектор принимаемой смеси сигнала и шума описывает своим концом траекторию вокруг начала координат, как показано на рис. 5.30, ж. Это вызывает фазовую ошибку величиной 2π (перескок на один период или цикл). Если такое движение совершается быстро, то его можно приближенно считать скачком фазы, который ведет к появлению кратковременного импульса мгновенной частоты, как показано на рис. 5.30, з. Колебание этого вида подается на вход фильтра нижних частот. Интуитивно ясно, что его можно рассматривать как сумму двух компонент – импульсной последовательности, обусловленной тем, что конец результирующего вектора описывает траектории вокруг начала координат, и флуктуационного шума, который можно исследовать методами линейного анализа. Компонента перескоков фазы обладает равномерным спектром с плотностью (2π)2fs, где fs – математическое ожидание числа перескоков в секунду (средняя интенсивность перескоков).
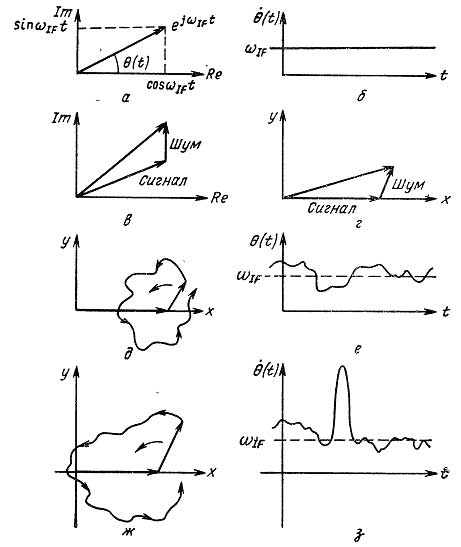
Рисунок 5.30 Векторные диаграммы
а – вектор сигнала; б – мгновенная частота, в – векторы сигнала и шума, г – вращающаяся координатная система (несущая исключена); д – малый уровень шума (не наблюдается траекторий конца результирующего вектора, охватывающих начало координат); е – мгновенная частота; ж – большой уровень шума (наблюдаются траектории конца результирующего вектора, охватывающие начало координат); з – мгновенная частота.
Райс вывел аналитическое выражение для этой величины, имеющее вид:
В этом выражении: p – отношение сигнал/шум на выходе фильтра ПЧ, R – радиус гирации фильтра ПЧ:
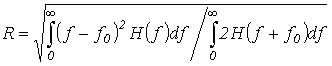 (161)
(161)