Аннотация
Предложен инвариантный к полосе частот принимаемого сигнала метод оценки отношения сигнал/шум, основанный на определении отношения частоты появления аномальных ошибок к среднему числу максимумов сигнала на выходе частотного детектора.
I. Введение
В радиотехнических системах различного назначения (радиолокационные, радионавигационные, системы связи, информационно–измерительные системы) актуальной является задача оценки отношения сигнал/шум в принятом радиосигнале. Существующие методы оценки требуют предварительного знания полосы частот, занимаемой принимаемым сигналом или введения в передаваемый сигнал специальных дополнительных сигналов. В данной магистерской работе рассмотрен метод оценки отношения сигнал/шум для сигналов с непрерывной несущей, свободный от указанных недостатков.
II. Постановка задачи
Прием полезных сигналов с непрерывной несущей сопровождается шумами. При этом если рассмотреть мгновенную частоту такой суммы полезного сигнала и шума, то можно отметить, что имеются две составляющие: небольшие флуктуации и короткие выбросы большой амплитуды [1].
Для облегчения понимания данного процесса предположим, что несущая сигнала немодулирована. Её можно представить как вращающийся вектор с фазой Θ(t) и длиной Um(t), равной амплитуде. Частота сигнала есть просто угловая скорость вращения этого вектора.
Вектор шума складывается с сигнальным вектором, как показано на рис. 1, а. Поскольку сигнальный вектор вращается с постоянной скоростью, для удобства представления можно просто отображать лишь относительное вращение результирующего вектора относительно сигнального вектора (рис. 1, б).

Рисунок 1. а) – векторное представление суммы сигнала и шума; б) – относительное векторное представление суммы сигнала и шума с учетом частоты несущей
Когда вектор шума мал, как показано на рис. 2, а, он вызывает незначительные флуктуации мгновенной частоты, как показано на рис. 2, б.

Рисунок 2. а) – годограф вектора суммы гармонического сигнала и шума, когда вектор шума мал по сравнению с сигнальным вектором; б) – частота суммы гармонического сигнала и шума
Если вектор шума велик, то результирующий вектор принимаемой смеси сигнала и шума описывает своим концом траекторию вокруг начала координат (рис. 3, а). Это вызывает фазовую ошибку величиной 2π (перескок на один период или цикл). Если такое движение совершается быстро, то его можно приближенно считать скачком фазы, который ведет к появлению кратковременного импульса мгновенной частоты большой амплитуды, как показано на рис. 3, б.

Рисунок 3. а) – годограф вектора суммы гармонического сигнала и шума, когда вектор шума велик по сравнению с сигнальным вектором; б) – частота суммы гармонического сигнала и шума
Это явление называется аномальной ошибкой [1]. При этом мгновенная частота такой суммы представляется импульсной последовательностью, обусловленной тем, что конец результирующего вектора описывает траектории вокруг начала координат, и флуктуационного шума, который можно исследовать методами линейного анализа. Компонента перескоков фазы обладает равномерным спектром с плотностью (2π)2fs, где fs – математическое ожидание числа перескоков в секунду (средняя интенсивность перескоков), определяется по формуле:
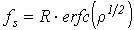 (1)
(1)
В этом выражении: p – отношение сигнал/шум на выходе фильтра ПЧ, erfc() – дополнительная функция ошибки, которая определяется выражением:
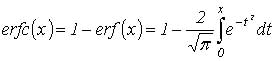 (2)
(2)
R – радиус гирации фильтра ПЧ:
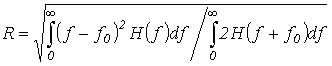 (3)
(3)
В выражении (3) f0 – несущая частота, H – передаточная характеристика фильтра [1].
Принимая передаточную характеристику фильтра ПЧ равномерной в пределах [ f0 – Δ f/2; f0 + Δf/2], из (3) получим следующий результат для радиуса гирации:
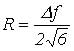
Из последнего выражения видно, что число аномальных ошибок зависит от полосы частот занимаемой сигналом, поэтому представляет интерес разработка метода оценки относительной частоты появления аномальных ошибок, инвариантного к полосе частот.
Определим среднее число максимумов N1max случайной частоты суммы сигнала и шума (рис. 2. б), считая спектральную плотность шума равномерной в полосе частот Δf с равномерным распределением фазы в пределах от –π до π. Нетрудно заметить, что спектральная плотность флуктуаций фазы суммы гармонического сигнала и шума будет также прямоугольна, но ее полоса будет составлять Δf/2.
В [2] определено соотношение для среднего числа максимумов для флуктуаций фазы квазигармонического процесса как:
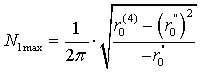 (5)
(5)
где r0 – корреляционная функция процесса r(τ) при τ = 0; r0″ и r0(4) – производные r(τ) при τ = 0 второго и четвертого порядка соответственно.
Учитывая причинно–следственную связь, очевидно, что среднее число экстремумов для флуктуаций фазы и частоты будет совпадать, поскольку частота является производной фазы.
Приняв, что функция изменения частоты (рис. 2, б) имеет равномерный спектр в полосе частот от 0 до 2π, ее корреляционную функцию можно представить в виде:
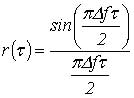
Вычислив производные и подставив в (5) получим:
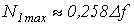
Разделив (4) на полученное соотношение, получим выражение инвариантное по отношению к полосе частот, занимаемой анализируемым сигналом:
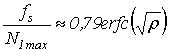
Таким образом, отношение сигнал/шум будет определятся по формуле:
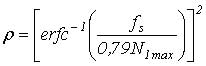 , (6)
, (6)
где erfc–1() – обратная дополнительная функция ошибки
График этой зависимости представлен на рис. 4.
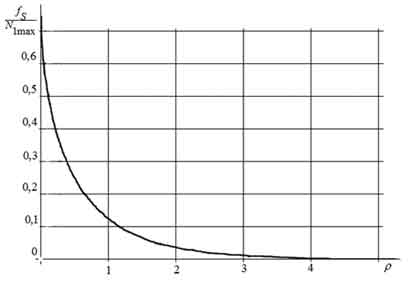
Рисунок 4. График зависимости отношения числа аномальных ошибок к среднему числу максимумов флуктуации частоты от отношения сигнал/шум
III. Результаты
Предложенный метод оценки отношения сигнал/шум, основанный на нахождении отношения частоты появления аномальных ошибок (кратковременных импульсов мгновенной частоты большой амплитуды) к общему числу экстремумов (выбросов) частоты сигнала, является инвариантным к полосе частот, занимаемой принимаемым сигналом. Он не требует предварительной оценки полосы частот, занимаемой принимаемым сигналом, что в конечном итоге приводит к уменьшению времени, необходимого для оценки отношения сигнал/шум.
Литература
- Ван Трис, Г. Теория обнаружения, оценок и модуляции. В 3 т., т. 2. Теория нелинейной модуляции / Г. Ван Трис; пер. с англ. В. Т. Горяинов. – М.: Советское радио, 1975. – 344 с.: ил.
- Тихонов, В. И. Выбросы траекторий случайных процессов / В. И. Тихонов, В. И. Хименко. – М.: Наука, 1987. – 304 с.: ил.