Аннотация
Предложен инвариантный к полосе частот принимаемого сигнала метод измерения отношения сигнал/шум, основанный на определении отношения частоты появления аномальных ошибок к среднему числу максимумов сигнала на выходе частотного детектора.
1. Введение
Существующие методы оценки требуют предварительного знания полосы частот, занимаемой принимаемым сигналом или введения в передаваемый сигнал специальных дополнительных сигналов. В данной магистерской работе рассмотрен метод оценки отношения сигнал/шум для сигналов с непрерывной несущей, свободный от указанных недостатков.
2. Основная часть
Сигнал на выходе частотного детектора можно рассматривать как сумму двух компонент – выбросов, обусловленных наличием разрывов фазы и флуктуационного шума [1]. Компонента разрывов фазы обладает равномерным спектром с плотностью (2π)2fs, где fs – математическое ожидание числа перескоков в секунду (средняя интенсивность перескоков), определяется по формуле:
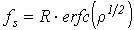 (1)
(1)
В этом выражении: p – отношение сигнал/шум на выходе фильтра ПЧ, erfc() – дополнительная функция ошибки, которая определяется выражением:
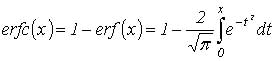 (2)
(2)
R – радиус гирации фильтра ПЧ:
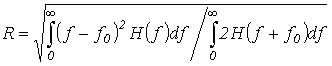 (3)
(3)
В выражении (3) f0 – несущая частота, H – передаточная характеристика фильтра [1].
Принимая передаточную характеристику фильтра ПЧ равномерной в пределах [ f0–Δf/2; f0 + Δf/2], и, подставив (3) в (1), получим:
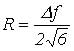
Подставив это в выражение (1), получим:
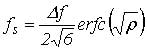 (4)
(4)
В [2] определено соотношение для среднего числа максимумов в единицу времени для флуктуаций фазы квазигармонического процесса как:
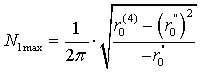 (5)
(5)
где r0 – корреляционная функция процесса r(τ) при τ = 0; r0″ и r0(4) – производные r(τ) при τ = 0 второго и четвертого порядка соответственно.
Корреляционную функцию изменения частоты можно представить в виде:
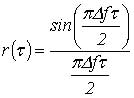
Вычислив производные и подставив последнее выражение в (5) получим:
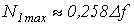
Разделив (4) на полученное соотношение, получим выражение инвариантное по отношению к полосе частот, занимаемой анализируемым сигналом:
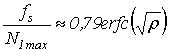
Таким образом, отношение сигнал/шум будет определятся по формуле:
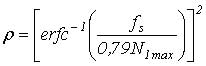 , (6)
, (6)
где erfc–1() – обратная дополнительная функция ошибки
На рис. 1 показана зависимость отношения числа аномальных ошибок в единицу времени к среднему числу максимумов флуктуации частоты в единицу времени от отношения сигнал/шум
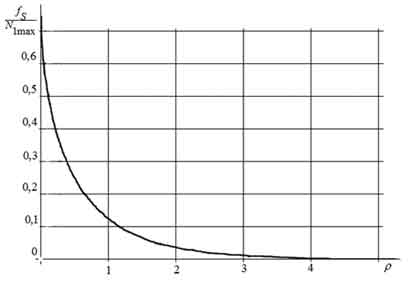
Рисунок 4. График зависимости отношения числа аномальных ошибок к среднему числу максимумов флуктуации частоты от отношения сигнал/шум
3. Заключение
Предложенный метод измерения отношения сигнал/шум, основанный на нахождении относительной частоты появления аномальных, является инвариантным к полосе частот, занимаемой принимаемым сигналом. Он не требует предварительной оценки полосы частот, занимаемой принимаемым сигналом, введения в исходный сигнал дополнительных опорных сигналов.
Литература
- Ван Трис, Г. Теория обнаружения, оценок и модуляции. В 3 т., Т. 2. Теория нелинейной модуляции / Г. Ван Трис; пер. с англ. В. Т. Горяинов. – М.: Советское радио, 1975. – 344 с.: ил.
- Тихонов, В. И. Выбросы траекторий случайных процессов / В. И. Тихонов, В. И. Хименко. – М.: Наука, 1987. – 304 с.: ил.