Аннотация
В работе рассматриваются вопросы анализа и синтеза устройств оценки отношения сигнал/шум, основанные на анализе фазовых флуктуаций аддитивной смеси, применительно к различным радиотехническим и контрольно–измерительным системам. Использованные методы, базируются на анализе вероятностных характеристик флуктуаций фазы и периода исследуемых сигналов.
Ключевые слова:
фазовые флуктуации, устройства оценки отношения сигнал/шум, погрешности измерений.
Abstract
The work deals with the analysis and synthesis of devices evaluation of the signal/noise ratio, based on the analysis of the phase fluctuations of the additive mixture, applied to various radio and instrumentation systems. The methods used are based on the analysis of the probability characteristics of phase fluctuations and the period investigated signals.
Key words:
phase fluctuations, device evaluation of the signal/noise ratio, the measurement error.
I. Введение
Одной из простейших распространенных аналитических моделей исследуемых процессов, используемых в различных радиосистемах, является аддитивная смесь гармонического сигнала и узкополосного случайного процесса, центральная частота энергетического спектра которого в частном, но широко распространённом на практике, случае совпадает с частотой гармонического сигнала и имеет вид [1]:
где Um, ω0, φ0 – амплитуда, угловая частота и начальная фаза сигнала, которые в общем случае могут быть модулированы полезным сообщением, а Α(t) и θ(t) – огибающая и фаза случайного процесса ξ(t).
Рассматриваемую модель аддитивной смеси можно наблюдать, например, на выходе блока усилителя промежуточной частоты и аналитически представить в виде:
где U(t), φ(t) и Φ(t) – случайные огибающая, фаза и полная фаза аддитивной смеси. Случайный характер процесса φ(t) обусловлен в основном аддитивным шумом, а статистические характеристики зависят от отношения сигнал/шум и определяются интенсивностью фазовых флуктуаций. Поэтому, выполняя оценку мощности фазовых флуктуаций можно определить сложившееся отношение сигнал/шум. Достаточно полное вероятностное описание характера изменения параметров сигнала может быть получено на основе известной информации о совместной многомерной плотности распределения огибающей аддитивной смеси, фазы и их производных [1]:
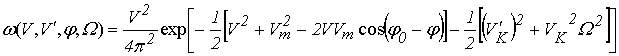
где V=U/σξ – нормированная амплитуда огибающей аддитивной смеси; Vm=Um/σξ – нормированная амплитуда сигнала; Vk=U/σKξ и Vk′=U′/σKξ – нормированные значения амплитуд огибающей и квадратурных составляющих производных, Ω – случайная частота, характеризующая скорость изменения фазы, а σξ и σKξ – среднеквадратические значения случайного процесса ξ(t) и его квадратурной составляющей.
Как следует из формулы, фаза исследуемой смеси влияет на характер и общую оценку совместного распределения амплитуды, фазы и их производных и определяет флуктуации измеряемых частотно-временных параметров. Из этой формулы можно найти плотности распределения, позволяющие характеризовать фазу и случайную частоту статистически, определяя наиболее вероятные значения и интенсивность их разброса, а также исследуя характерные зависимости от различных параметров и использовать их для оценки помехоустойчивости радиотехнических систем.
Для получения совместной плотности распределения случайной фазы аддитивной смеси и случайной частоты следует выполнить двойное интегрирование многомерной плотности распределения ω(V, V′, φ, Ω) по всем значениям огибающей и её производной:
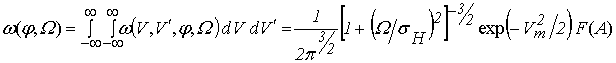
В этом выражении:
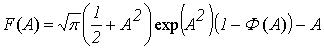
σH=σKξ/σξ – нормированное среднеквадратическое значение квадратурных составляющих, Φ(A) – интеграл вероятности. На рис. 1 приведён график поверхности, характеризующий это совместное распределение при изменении исследуемых переменных в диапазоне от –π до π. Совместная плотность распределения случайной фазы и частоты концентрируется в области нулевых значений переменных φ и Ω, определяя экстремумом наиболее вероятные значения рассматриваемых случайных процессов. Вероятность этих значений увеличивается с возрастанием Vm, а совместное распределение стремится в пределе к графику поверхности дельта–функции.
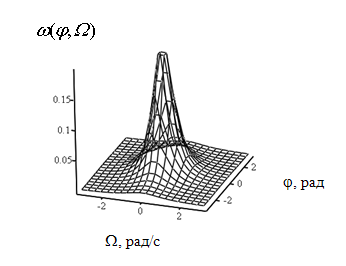
Рисунок 1. Совместная плотность распределения случайных фазы и частоты при Vm=1
При стационарных флуктуациях фазы исследуемого сигнала плотность распределения фазы может быть представлена рядом Фурье вида [1]:
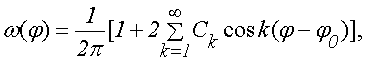
В этом выражении:
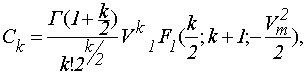
Г(·) – гамма-функция; 1Г1(·) – вырожденная гипергеометрическая функция, а нормированную амплитуду огибающей аддитивной смеси и нормированную амплитуду сигнала можно представить как V=U/σ, Vm=Um/σ, где σ2=W0·Fэ – мощность шума в рассматриваемой системе, W0 – интенсивность энергетического спектра шума действующего на входе, а Fэ – эффективная полоса пропускания анализируемой системы. Безусловная плотность распределения полностью определяется коэффициентами, Ck, значения которых зависят от нормированных амплитуд V, Vm.
Безусловное распределение определяет величину среднеквадратического значения фазовых флуктуаций (рис. 2) и в основном участками суммарного процесса с малыми значениями огибающей аддитивной смеси, вероятность появления которых ω(V) достаточно велика и имеет существенное значение, поскольку,
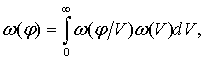
где ω(φ/V) – условная плотность распределения фазы аддитивной смеси.
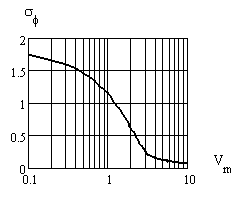
Рисунок 2. Зависимость среднеквадратического значения фазовых флуктуаций от отношения сигнал/шум.
2. Построение устройств оценки отношения сигнал/шум на основе фазовых флуктуаций сигнала
На основе анализа вероятностных характеристик фазовых флуктуаций аддитивной смеси разработано устройство измерения отношения сигнал/шум [2], упрощённая структурная схема которого приведена на рис. 3.
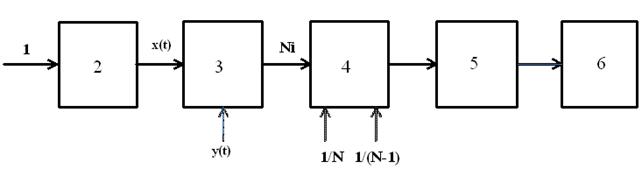
Рисунок 3. Структурная схема измерения отношения сигнал/шум.
(2 – приёмник, 3 – измеритель фазы,
4 – блок вычисления дисперсии фазы, 5 – блок вычисления отношения сигнал/шум, 6 – блок индикации и
дополнительной обработки)
В соответствии со структурной схемой аддитивная смесь полезного сигнала и узкополосного шума формируется в приёмнике 2 и поступает на измеритель фазы 3, где выполняется преобразование фазового сдвига между сигналами x(t) и y(t) во временной интервал, который заполняется счётными импульсами. Результат измерения фазы представляет собой числа Ni, которые подвергаются статистической обработке для определения дисперсии фазы по формуле, обеспечивающей несмещённую оценку:
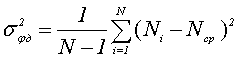
где Ni – цифровые отсчёты фазы, N – количество усредняемых отсчётов, Ni – среднее численное значение фазы смеси. Полученная формула при N>>1 преобразуется к виду, удобному для практической реализации:
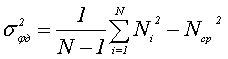 (1)
(1)
В рассматриваемом устройстве для заданного диапазона значений дисперсии фазы, соответствующих определённому значению отношения сигнал/шум (рис. 2), предварительно выполняется расчёт, результаты которого помещаются в запоминающее устройство блока вычисления отношения сигнал/шум с необходимой дискретностью и по результатам нахождения дисперсии фазовых флуктуаций (1) определяется отношение сигнал/шум.
3. Построение устройств оценки отношения сигнал/шум на основе измерения флуктуаций периода
Перспективным вариантом измерения отношения сигнал/шум является способ измерения отношения сигнал/шум [3], позволяющий
оценить помехоустойчивость различных радиосистем, при котором разбивают суммарный интервал времени измерения на отдельные внутренние
временные интервалы, содержащие целое число периодов входного сигнала и периодов сигнала эталонной частоты, укладывающихся в пределах каждого
внутреннего временного интервала, определяют квадрат среднего значения периода входного сигнала за суммарный интервал времени измерения,
вычисляют дисперсию временного интервала числа периодов входного сигнала, а значения отношения сигнал/шум (по мощности) определяют по
формулам [3]:
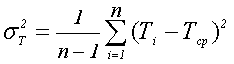 (2)
(2)
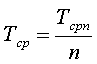 (3)
(3)
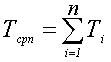 (4)
(4)
где σT2 – дисперсия временного интервала числа n периодов входного сигнала Tcp2 – квадрат среднего значения периода входного сигнала за суммарный интервал времени измерения, Tcpn – среднее значение временного интервала числа n периодов, укладывающихся в пределах каждого внутреннего временного интервала; n – число периодов, укладывающихся в пределах каждого внутреннего временного интервала, Ti – численные результаты отсчётов i-го периода.
Полученные значения поступают на индикатор или на персональный компьютер для дополнительной обработки.
Для пояснения работы такого метода измерения отношения сигнал/шум, рассмотрим вариант построения устройства, структурная схема которого приведена на рис. 4.

Рисунок 4. Структурная схема устройства измерения отношения сигнал/шум.
(1 – измеритель временных
интервалов, 2 – блок вычисления дисперсии временных интервалов, 3 – блок вычисления отношения сигнал/шум,
4 – индикатор)
На рис. 5 приведён вариант построения блока вычисления дисперсии временных интервалов.
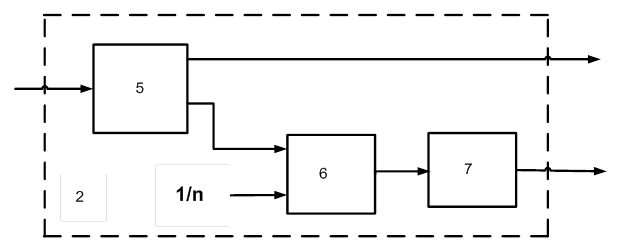
Рисунок 5. Структурная схема блока вычисления дисперсии
(5 – измеритель средних значений временных
интервалов, 6 – блок вычисления дисперсии, 7 – квадратор)
При практической реализации используется рабочая формула оценки отношения сигнал/шум по мощности, зависящая от параметров оценки временных интервалов [3]:
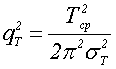
На основании реализации (5), измеритель временных интервалов 1 (рис. 4) формирует и измеряет внутренние временные интервалы с постоянным целым числом периодов, причём длительность внутреннего временного интервала должна быть больше интервала корреляции обрабатываемой аддитивной смеси, обеспечивая независимость отсчётов.
Результатом измерения являются цифровые отсчёты, которые соответствуют длительности i-го внутреннего временного интервала Ti. В каждом внутреннем временном интервале укладывается n периодов обрабатываемой аддитивной смеси. Измеритель внутреннего временного интервала 1 может быть выполнен как классический частотомер.
Цифровые отсчёты, получаемые на выходе измерителя внутреннего временного интервала 1, поступают на вход блока вычисления дисперсии временных интервалов 2, где подвергаются статистической обработке для определения дисперсии длительности временных интервалов и квадрата среднего значения длительности периода обрабатываемой смеси. Работа устройства вычисления дисперсии временных интервалов 2 основана на использовании способа обработки результата n измерений длительности временных интервалов, обеспечивающего несмещенную оценку (2).
Полученные значения с выхода блока вычисления дисперсии 2 преобразуются согласно приведенным формулам в величину qT2, определяющую отношение сигнал/шум в блоке 3, который реализуется из последовательно соединенных делителя и умножителя, а полученный результат поступает на индикатор 4 или в ПК для последующей обработки.
4. Выводы
Рассмотрены варианты построения устройств оценки отношения сигнал/шум, основанные на определении интенсивности фазовых флуктуаций обрабатываемой аддитивной смеси в различных радиотехнических системах, а также на оценках статистических характеристик периода исследуемого сигнала. Получены алгоритмы оценки отношения сигнал/шум и разработаны устройства, позволяющие повысить точность оценки и упростить реализацию устройства, что в конечном результате позволяет вести оперативный контроль над измеряемыми параметрами сигналов и повысить помехоустойчивость радиотехнических систем.
Литература
- Левин, Б. Р. Теоретические основы статистической радиотехники / Б. Р. Левин. М.: Радио и связь, 1989. – 656 с.: ил.
- Пат. 2341808 Российская Федерация, МПК G 01 R 29/26. Устройство измерения отношения сигнал/шум / Леглер В. В., Патюков В. Г., Патюков Е. В.; заявитель и патентообладатель Федеральное государственное образовательное учреждение высшего профессионального образования Сибирский федеральный университет. – № 2007117230/28 ; заявл. 08.05.2007 ; опубл. 20.12.2008, Бюл. № 35. – 6 с.: ил.
- Пат. 2399923 Российская Федерация, МПК G 01 R 29/26. Способ измерения отношения сигнал/шум / Леглер В. В., Патюков В. Г., Патюков Е. В.; заявитель и патентообладатель Федеральное государственное образовательное учреждение высшего профессионального образования Сибирский федеральный университет. – № 2007117230/28 ; заявл. 02.03.2009 ; опубл. 20.09.2010, Бюл. № 26. – 5 с.: ил.