ИССЛЕДОВАНИЕ ВЛИЯНИЯ УГЛА СТОЛКНОВЕНИЯ С ЧАСТИЦЕЙ НА ТРАЕКТОРИЮ ДВИЖЕНИЯ ВОЗДУШНОГО ПУЗЫРЬКА ПРИ ОБОГАЩЕНИИ МИНЕРАЛОВ
Авторы: Назимко Е.И., Друц В.И.
Источник:Матеріали VII науково-практичної конференції.
Донбас-2020: перспективи розвитку очима молодих вчених.
АННОТАЦИЯ
У даній роботі розглянута комп'ютерна модель для моделювання кінетики взаємодії фаз при збагаченні. В ході проведення імітаційного експерименту було поставлено завдання визначення параметрів взаємодії частинок і бульбашок при утворенні флотаційного комплексу. Проведені дослідження впливу кута зіткнення з частинкою на траєкторію руху повітряної бульбашки, отримання дані продемонстрували прийнятну поведінку комп'ютерної моделі при моделюванні окремих стадій процесу взаємодії фаз при збагаченні флотації і довело її ефективність.
ОБЩАЯ ПОСТАНОВКА ПРОБЛЕМЫ
Основные технологии процессов обогащения связаны со взаимодействием фаз. Типичным примером может быть взаимодействие воздушных пузырьков с реагентами и минералами, благодаря чему происходит их флотация [1]. Эти взаимодействия представляют значительную трудность для исследования, т.к. они динамичны, находятся под влиянием большого массива физических и химических факторов и происходят в маленьком масштабе. Одним из мощных вариантов разрешения этой проблемы является численное моделирование, которое сочетает в себе динамику, точность и рассмотрение широкого спектра деталей.
В данной работе рассматривается компьютерная модель для моделирования кинетики взаимодействия фаз при обогащении, которая базируется на дискретных элементах. Модель принимает к рассмотрению эффект упругости твердого, воды и воздушной фазы, прочность связей между ними, динамическое сопротивление или демпфирование фаз, рассеивание кинетической энергии при столкновениях, силы тяжести, магнитные и центробежные силы, перемещения, граничные и начальные условия. Настройка модели была выполнена для времени прикрепления при взаимодействии частиц и воздушных пузырьков, их деформаций, траекторий, скоростей и ускорений. Метод дискретных элементов был первоначально развит в геомеханике для моделирования поведения пород под действием горного давления [2, 3]. Этот метод был позже успешно применен для описания взаимодействия частиц породы и течения потоков [4, 5, 6]. Данная модель базируется на том же приближении, что и модели, представленные в работах [3, 4, 5].
Кроме того были учтены существенные особенности процессов обогащения. Разделяемые частицы имеют действительно комплексное поведение в процессах обогащения по сравнению с поведением массива пород. Они двигаются и подвергаются множественным актам слипания и разрушения флотационных комплексов. Эти процессы управляются физическими и химическими свойствами поверхности минералов и реагентов. Рассмотрим пару минеральных частиц, взаимодействие которых представлено на рис. 1.
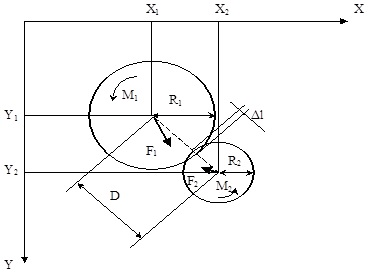
Рисунок 1 – Модель взаимодействия двух элементов
Частицы имеют шарообразную форму с радиусами R1 и R2. Любая частица движется под действием силы (F1 или F2) и вращается в соответствии с законом Ньютона в прямоугольной системе координат X-Y, если она ускоряется моментами M1 и M2. Движения разделяемых частиц рассматриваются в дискретные периоды времени. В компьютерной реализации эти периоды моделируются как циклы. Координаты центров тяжести X1, Y1 и X2, Y2, скорости V1 и V2, и силы являются постоянными и рассчитываются на каждом цикле. Более подробно работа модели описана в работе [7]. Модель позволяет рассчитывать приращение скорости частиц и параметры взаимодействия в различные моменты времени.
В течение каждого цикла смежные частицы проверяются на условия когезии и адгезии. Если частицы имеют приближение одна к другой на критическое расстояние, они слипаются между собой (две или несколько). Одновременно проверяются силы адгезии (когезии). Если они достигают определенных пределов, слипшиеся комплексы разрушаются.
Таким образом моделируется правдивое динамическое поведение минералов при их обогащении. Для возможности качественного сравнения результатов имитационного моделирования и натурного эксперимента было выполнено компьютерное моделирование закрепления частицы на пузырьке для следующих условий. Угольная частица диаметром 0.29 мм падала со скоростью 0.3 мм / с на воздушную пузырь диаметром 2 мм, истекающего со скоростью 12 мм / с. Точка встречи смещалась относительно центра пузыри на 100, 200, 300, 400, 500, 600, 700, 800 , 900 и 1000 микрон. Это смещение может быть рассмотрено как эксцентриситет относительно центра и направления силы тяжести. Начальная модель представлена на рис. 2.
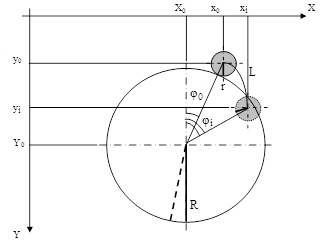
Рисунок 2 – Исходная схема для моделирования
Здесь показаны: x0 - X0 = e - эксцентриситет при встрече частицы и пузырьки, Φ0 і Φi - начальный угол касания частицы и текущий, соответственно; R и r - положение радиуса пузырька и частицы, соответственно; L - дуговой путь центра тяжести частицы; а также координаты центров тяжести пузырьки и частицы.
Процесс взаимодействия частицы, падает, и всплывающей вверх пузырек моделировался в течение 80000 циклов. Один цикл счета отвечал 10-6с натурального времени.
Координаты центров тяжести элементов и состояние комплекса накапливались в файле каждые 200 циклов. Для расчетов принято взаимодействие воздушного пузырька диаметром 2.5мм (2000 пикселей) и угольной частицы размером 0.36мм (290 мкм) сферической формы.
Исследования, проведенные ранее с применением компьютерного моделирования, позволили установить, что при столкновении воздушного пузырька и минеральной частицы тангенциальная компонента скорости частицы возрастает с увеличением эксцентриситета между центром пузырька и точкой встречи с частицей. Именно эта компонента скорости при увеличении до критического значения вызывает проскальзывание частицы относительно поверхности пузырька и в итоге ее отрыв.
Кроме того, определенный интерес представляют другие параметры перемещения частицы относительно пузырька и комплекса в целом.
На рис. 3 представлены расчетные графики траекторий перемещения центра тяжести частицы без учета всплытия пузырька.
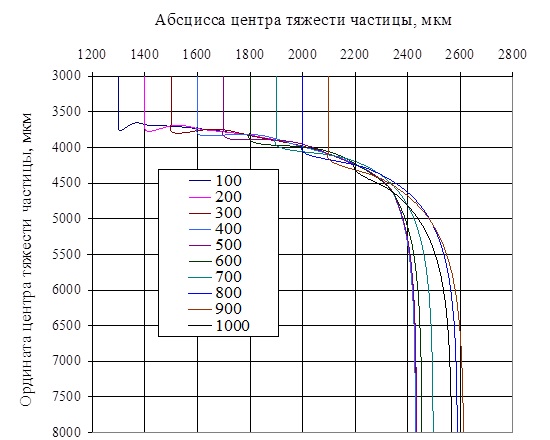
Рисунок 3 – Траектория центра тяжести частицы без учета всплывания пузырька при различных эксцентриситетах столкновения
Вертикальные линии на рис. 3 соответствуют траектории движения частицы до столкновения с пузырьком. При образовании агрегата флотации частица закрепляется на пузырьке и движется по его поверхности или вместе с ним. Затем происходит отрыв частицы при эксцентриситете встречи 100 и 1000 пикселей, то есть 125 и 1250 мкм или при угле столкновения от 5 до 65°.
ВЫВОДЫ
Таким образом, проведенные исследования кинетики взаимодействия фаз при флотационном обогащении путем компьютерного моделирования и сравнение результатов расчета и экспериментов показали приемлемую сходимость. Как следует из данных, максимальное время существования комплекса флотации и совместного движения частицы и пузырька наблюдается при минимальном значении угла столкновения.
СПИСОК ЛИТЕРАТУРЫ
1. S. S. Kim, B. I. Morsi, and
S.–H. Chiang, Statistical Analysis of the Performance of a
Selective Agglomeration Process Using n-heptane as Agglomerant, Coal
Preparation, 15, 51-70 (1994).
2. P. A. Cundall, O. D. L. Strack, A discrete numerical model for
grannular assemblies, Geotechnique, 29:1, 47–65 (1979).
3. Звягильский Е.Л. Изучение кинетики обрушения толщи над
горизонтальными выработками мелкого заложения // Проблемы горного
давления. – 1999. - № 2. – С. 17-29.
4. Bruno M. S. et al. 1996. Some influences of saturation and fluid
flow on sand production: Laboratory and Discrete Element Model
Investigations. SPE 36534, Proc. 1996 SPE Ann. Tech. Conf., Denver,
Colorado, 6–9 October, 447–461.
5. O'Connor P.M., John R. Torczynski Dale S. Preece; Justin T. Klosek;
John R. Williams Discrete Element Modeling of Sand Production Int. J.
Rock Mech. & Min. Sci. 34:3–4, Paper No. 231.
6. P. F. Whelan and D. J. Brown, Particle-Bubble Attachment in Froth
Flotation, Bull. Inst. Min. a. Met., No 591, 593 (1956).
7. Е.Е. Гарковенко, Е.И. Назимко, А.И Самойлов и др. Особенности
флотации и обезвоживания тонкодисперсных углесодержащих материалов.
– Донецк: Норд-пресс. – 2002. – 256 с.
8. С.И. Митрофанов. Селективная флотация. М.: Металлургиздат. - 1958.
– 726 с.