МОДЕЛИРОВАНИЕ ВЛИЯНИЯ СКОРОСТИ ВЗАИМОДЕЙСТВУЮЩИХ ЧАСТИЦ И ПУЗЫРЬКОВ НА ВОЗМОЖНОСТЬ ОБРАЗОВАНИЯ ФЛОТАЦИОННОГО КОМПЛЕКСА
Автор: Звягинцева Н.А.
Источник:Науково-технічний журнал «Вісті Донецького гірничого інституту».
Проблема и ее связь с научными и практическими задачами.Уголь представляет собой ценное сырье для дальнейшей химической переработки с целью получения необходимых для промышленности продуктов, а также является одним из главных источников получения тепловой энергии [1]. Современные углеобогатительные предприятия постоянно сталкиваются с проблемой обогащения шламов.
Флотация является в настоящее время единственным эффективным способом обогащения тонких классов каменного угля. Широкое промышленное развитие флотации угля обуславливается главным образом резким увеличением содержания этих классов в добываемом угле вследствие механизации его добычи.
Современный флотационный процесс, основанный на использовании физико-химических и физических явлений и регулируемый взаимодействием многих факторов, является одним из наиболее актуальных научно-технических исследований.
Анализ исследований и публикаций. Одним из важных факторов, определяющих вероятность протекания собственно флотации является образование флотационного комплекса "воздушный пузырек - угольная частица". При этом характер движения твердой фазы и воздушных пузырьков в значительной мере влияет на вероятность столкновения частиц с пузырьками, образование и успешное всплывание флотационных комплексов, что определяют в свою очередь скорость процесса сепарации при флотации.
Исследования многих авторов прошлых лет посвящены развитию теоретических основ процесса и разработке параметров процесса флотационного обогащения различного минерального сырья [2-4]. В настоящее время появился цикл работ, посвященных флотации углей [5-8]. Изучение элементарного акта флотации затрудняется высокой скоростью образования флотационного комплекса и влиянием большого числа различных параметров на этот процесс, особенно на микроуровне. Развитие компьютерных методов моделирования и исследования таких процессов позволяет лучше понимать природу многих явлений [6, 9].
Постановка задачи. Целью настоящей работы является исследование на микроуровне взаимодействия частиц угля с воздушными пузырьками при различных скоростях движения взаимодействующих элементов.
Изложение материала и результаты. Для исследования применялось численное моделирование с использованием дискретных элементов комплекс программ разработан в ДонНТУ в лаборатории Моделирования необратимых процессов. Методика моделирования и исходные условия более подробно описаны в работах [5-8].
Исходное состояние модели и текущее положение частицы на поверхности пузырька при их контакте представлено на рис. 1.
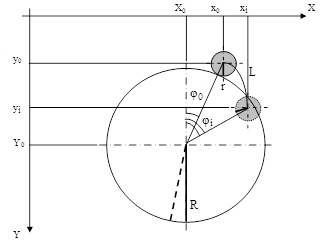
Рисунок 1 – Исходная модель и текущее положение частицы:
Х0, Y0; х0, y0 – координаты центров тяжести пузырька и частицы в начальный момент; R, r – радиусы пузырька и частицы; L – дуговой путь частицы; φ0, φi – начальный и текущий угол положения частицы; α2 – угол поворота радиуса частицы при движении по поверхности пузырька
Базовыми условиями для моделирования были приняты параметры, определенные оптимальными для образования флотационного комплекса, которые были опубликованы в работах последних лет [7-9]. Как было установлено в этих исследованиях, имеет место критическое значение угла встречи частицы и пузырька. При значениях угла встречи менее критического флотационный комплекс существует достаточно долго, что обеспечивает возможность выноса угольной частицы в пенный слой при заданных свойствах поверхности взаимодействующих элементов. Поэтому эти параметры и были приняты в качестве исходных.
В ходе изучения исследовалось взаимодействие падающей угольной частицы и всплывающего воздушного пузырька путем компьютерного моделирования в течение 80000 итераций (циклов счета). Один цикл счета соответствовал 10-6 с натурального времени. Координаты центров тяжести элементов накапливались в выходном файле через каждые 200 итераций, обработка цифровых данных позволяет определять состояние комплекса. Для расчетов принято взаимодействие воздушного пузырька и угольной частицы сферической формы с диаметрами 2,5 и 0,36 мм соответственно в выбранном масштабе в пикселях.
Численное моделирование дает возможность определять путем вычислений на базе обработки цифровых файлов изменение скорости и траектории движения участвующих во взаимодействии элементов. Таким образом можно моделировать поведение угольных частиц и воздушных пузырьков в процессе флотации.
Были рассчитаны параметры перемещения частицы относительно пузырька и комплекса в целом. Изучалось влияние ускорений частицы и пузырька на вероятность образования и сохранения флотационного комплекса.
Для расчетов приняты значения ускорений элементов в условных единицах; для воздушного пузырька: 2е8; 2,5е8; 2,9е8; 3е8; 3,1е8; для угольной частицы: 0,0001; 0,05; 0,5; 5е*; 5е2; 5е3; 5е4; 5е5; 1е6; 2е6; 2,5е6; 2,9е6; 3е6; 3,5е6; 4е6. Исследовались результаты взаимодействия элементов при различных сочетаниях скоростей и ускорений.
На основе данных моделирования построены графики изменения траектории перемещения частицы относительно пузырька в течение всего времени их взаимодействия в зависимости от ускорения обоих элементов, представленные на рис. 2-4.
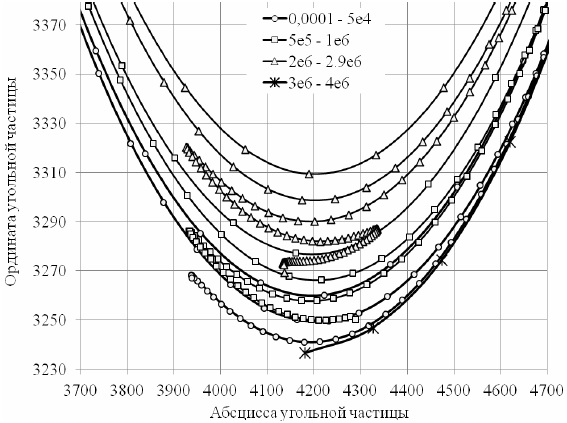
Рисунок 2 – Траектории перемещения угольной частицы относительно воздушного пузырька при его постоянном ускорении 3e8 усл. ед.
На основании проведенных исследований можно сделать вывод о том, что скорость движения пузырьков и частиц в пульпе значительно влияет на характер их перемещения и время существования флотационного комплекса. После падения на поверхность пузырька в верхней его части угольная частица скользит по его сферической поверхности и совершает колебания вправо-влево (витки) на нижней полусфере. При этом образовавшийся комплекс продолжает всплывать в пульпе вверх к пенному слою.
При постоянном ускорении пузырька равном 3е8 и небольших ускорениях частицы от 0,0001 до 5е4 угольная частица закрепляется на воздушном пузырьке, скользит по его нижней полусфере, постепенно уменьшая длину траектории, и отрывается на третьем витке. При повышении ускорений частицы до 1е6 количество витков скольжения увеличивается до четырех, при ускорениях от 2е6 до 2,9е6 – до пяти витков. При относительно больших ускорениях от 3е6 до 4е6 частица скользит по воздушному пузырьку и отрывается, не закрепляясь. Время существования флотационного комплекса соответственно составляет 0,264; 0,0288; 0,0358; 0,0092 с.

Рисунок 3 – Траектории перемещения угольной частицы относительно воздушного пузырька при постоянном ускорении частицы 0,05 усл. ед.
Анализируя данные, также следует отметить, что ускорение воздушного пузырька в большей мере влияет на время взаимодействия пузырька и частицы. При значениях ускорения угольной частицы 0,05 и 2,9е6 и ускорении пузырька 3е8 флотационный комплекс образуется, существует некоторое время. При таких же ускорениях частицы, но различных ускорениях пузырька (от 2е8 до 3,1е8) закрепления не происходит, частица только перемещается по его поверхности и соскальзывает с него на нижней полусфере.
Из приведенных данных (рис. 3 и 4) следует, что при принятых условиях (угол встречи, размер элементов и др.) и свойствах поверхностей взаимодействующих элементов имеет место определенный интервал значений скоростей элементов, при которых обеспечивается образование флотационного комплекса и его существование в течение некоторого времени.

Рисунок 4 – Траектории перемещения угольной частицы относительно воздушного пузырька при постоянном ускорении частицы 2,9е6
Выводы и направления дальнейших исследований.
На основании выполненных исследований можно заключить, что данная компьютерная модель на базе дискретных элементов дает представление о процессах, происходящих в ходе взаимодействии разных фаз при флотации, и может быть использована для их изучения на микроуровне.
При изменении динамических параметров участвующих в процессе элементов изменяется характер их перемещения и взаимодействия в среде.
При увеличении ускорений движения угольной частицы и воздушного пузырька уменьшается вероятность сохранения флотационного комплекса.
Наблюдаются определенные сочетания скоростей и ускорений элементов системы, при которых не происходит образование флотокомплекса. Существу ют критические значения скорости движения пузырьков и частиц, при которых процесс флотации становится маловероятным.
Дальнейшие исследования могут быть направлены на изучение практических последствий полученных эффектов.
СПИСОК ЛИТЕРАТУРЫ
1. Уголь в топливно-энергетическом балансе Украины и перспективы повышения его качества / Е.Е. Гарковенко, Е.И. Назимко, А.Н. Корчевский и др. // Збагачення корисних копалин: Наук.-техн. зб. – 2007. – Вип. 29(70)-30(71). – С. 14-19.
2. Теория и технология флотации руд. / Под общей ред. О.С. Богданова. – М.: Недра, 1990. – 364 с.
3. Физико-химические основы теории флотации. – М.: Наука, 1983. – 264 с.
4. Рубинштейн Ю.Б., Филиппов Ю.А. Кинетика флотации. – М.: Недра, 1980. – 376 с.
5. Назимко Е.И., Друц И.Н., Решетов В.П. Исследование процесса флотации с помощью компьютерной модели. Настройка модели. // Тр. междунар. науч.-техн. конф. "Горная энергомеханика и автоматика", посвященной 100-летию В.Г. Гейера. – Донецк, 2003. – Т.1. – С. 191-195.
6. Особенности флотации и обезвоживания тонкодисперсных углесодержащих мате-
риалов. / Е.Е. Гарковенко, Е.И. Назимко, А.И. Самойлов и др. – Донецк: Норд-Пресс, 2002. – 266 с.
7. Назимко Е.И., Друц И.Н., Серафимова Л.И. Исследование процесса флотации угольных частиц на микроуровне // Наукові праці Донецького національного технічного університету: Серія гірничо-електромеханічна. – 2008. – Вип. 15(131). – С. 115-121.
8. Назимко О.І., Серафімова Л.І. Моделювання впливу властивостей поверхні частинок на утворення флотаційного комплексу // Збагачення корисних копалин: Науч.-техн. зб. – 2009. – Вип. 38(79). – С. 104-110.
9. Nazimko L.I. Kinetics of Phases Interaction during Mineral Processing Simulation / L.I. Nazimko, E.E. Garkovenko, A.N. Corchevsky, I.N. Druts // Proceedings of XV International Congress of Coal Preparation. – China, 2006. – Р. 775-781.