Аннотация
Толочко О.И., Палис Ф., Бажутин Д.В. Гашение горизонтальных упругих колебаний конструкции мостового крана Выполнен анализ горизонтальных поперечных колебаний моста при его перемещении с неподвижной тележкой, закрепленной посередине моста, с помощью пакета Comsol Multiphysics. Разработана линейная математическая модель исследуемого объекта в виде двухмассовой механической системы. Синтезирован модальный регулятор, позволяющий гасить упругие колебания как в линейной модели, так и в модели с распределенными параметрами.
Актуальность работы
При исследовании крановых механизмов обычно уделяют внимание колебаниям груза и их гашению. Однако в процессе перемещения моста и тележки упругим деформациям подвергается мост, что приводит к сокращению срока его службы.
Целью данной работы является исследование и гашение горизонтальных колебаний моста при его перемещении.
Материал и результаты исследований
Применение сечений специальной формы позволяет создавать механические конструкции мостовых кранов, которые при относительно небольшой массе обладают достаточно высокой жесткостью. Однако с увеличением пролета податливость конструкции к воздействию упругих колебаний увеличивается.
Особенностью таких объектов является тот факт, что их масса и упругость равномерно распределены по длине конструкции, в результате чего процесс их упругой деформации описывается дифференциальными уравнениями в частных производных (ДУЧП). Для их математического моделирования удобно использовать специализированное программное обеспечение, предназначенное для решения задач механики деформируемого твердого тела, в частности, пакет Comsol Multiphysics, также известный как Femlab [1]. В среде этого пакета модель набирается в виде механической конструкции, а ДУЧП решаются методом конечных элементов.
Упрощенная модель конструкции моста в пакете Comsol Multiphysics приведена на рис.1. Параметрами этой модели являются геометрические размеры и массы моста и тележки, а также модуль упругости материала, из которого изготовлен мост.
Данная модель выполнена в виде сплошных металлических балок, что не соответствует действительности. Однако создание тонкостенных моделей усложняет модель и увеличивает требуемый объем оперативной памяти, а также время расчета переходных процессов.
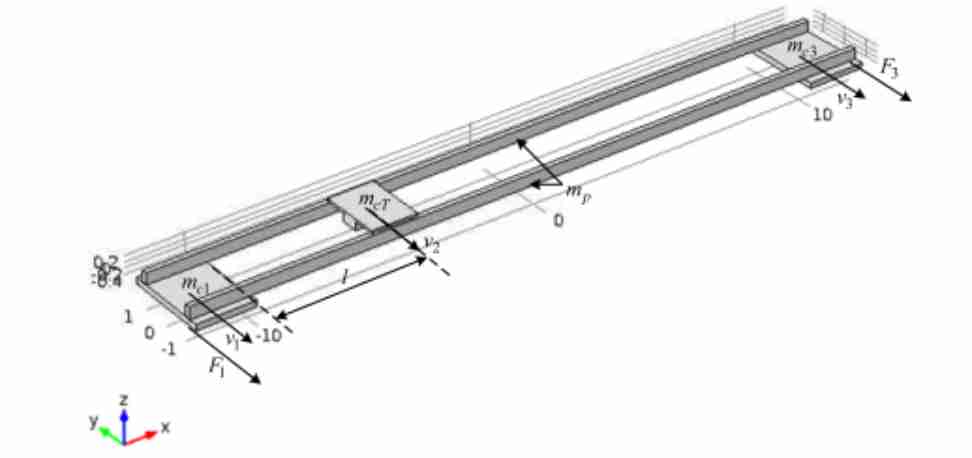
Рисунок 1 – Модель конструкции мостового крана
Поэтому с целью максимального упрощения модели мост представляем в виде двух цельнометал-лических профилей с прямоугольным сечением и заниженными значениями плотности и модуля упругости материала так, чтобы масса конструкции примерно соответствовала реальным данным. Тележка фиксируется в одном положении и моделиру-ется как составная часть конструкции моста.
Расположим тележку посредине моста и приложим к крайним граням данной конструкции усилие, соответствующее разгону моста до скорости 0.5 м/с за 1 с при отработке трапецеидального закона изменения скорости.
Графики изменения скорости крайних точек моста v1 и тележки v2, а также максимальной деформации моста в поперечном направлении Δs2,которая имеет место в его средней точке, приведены на рис.2. Из них видно, что рассматриваемые точки конструкции совершают незатухающие колебания, которые постепенно уменьшают ее прочность. На основании анализа частотного спектра сигнала скорости в пакете Comsol установлено, что наиболее ярко выраженными являются колебания конструкции с частотой f=1.18 Гц.
Для подавления этих колебаний необходимо синтезировать соответствующую систему управления скоростью моста, что требует наличия линейной математической модели объекта регулирования.
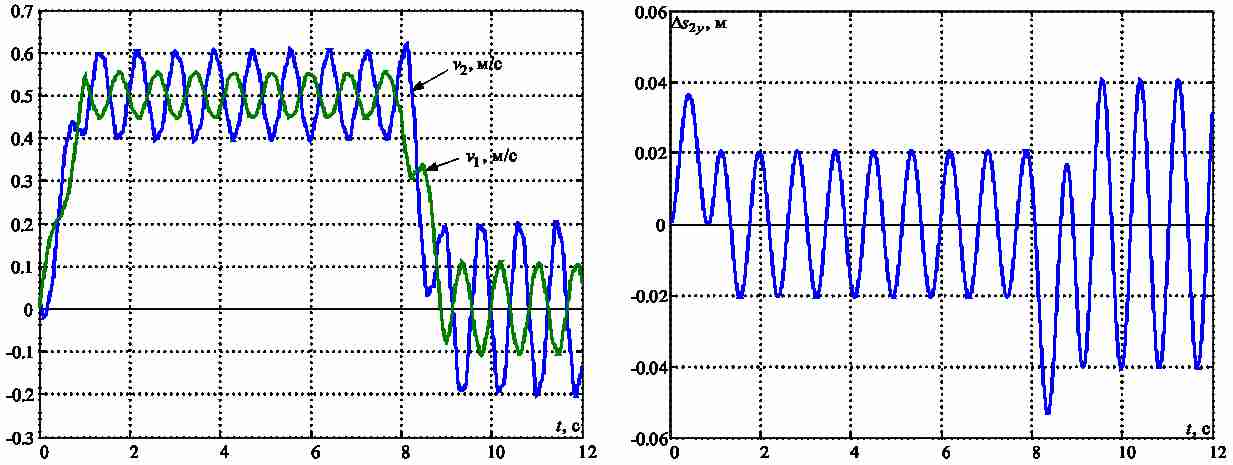
Рисунок 2 – Переходные процессы движения упругой конструкции мостового крана
В данном случае математическую модель объекта можно составить на основании кинематических схем многомассовых систем, приведенных на рис. 3.
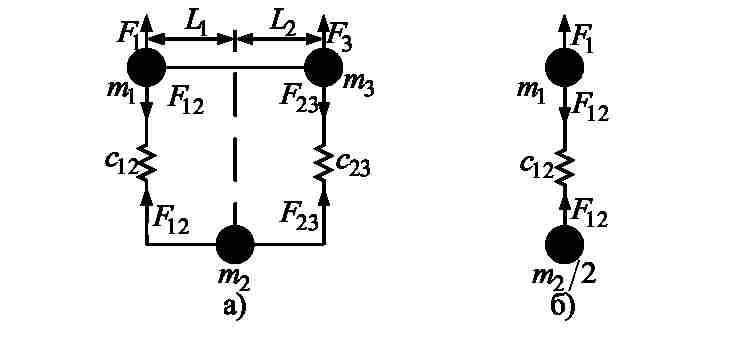
Рисунок 3 – Кинематические модели моста
На рис.3а мост условно представлен в виде трех сосредоточенных масс – крайних точек m1 и m3, связанными упругими связями с коэффициентами жесткости c12 и c23 с точкой m2, в которой находится тележка.
Если тележка расположена посередине моста (L1=L2), то и коэффициенты жесткости упругих связей также должны быть одинаковыми. Если при этом равны между собой и массы, сосредоточенные на концах моста, а также приложенные к ним силы, то одинаковом расстоянии от опор, массы которых равны, то кинематическую схему моста можно упростить до двухмассовой, оставив одну опору и центральную точку, массу которой следует уменьшить в 2 раза. Кинематическая схема для такого случая представлена на рис.3б. Ее математическое описание имеет вид:
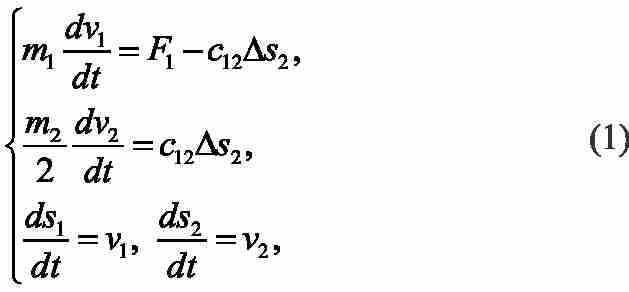
где F11 – сила, приложенная к первой массе, F12 – упругая сила, Δs2=s1-s2 – величина упругой деформации.
При известных значениях сосредоточенных масс и постоянной времени упругих колебаний двухмассовой системы T12=1/2πf можно рассчитать коэффициент жесткости:
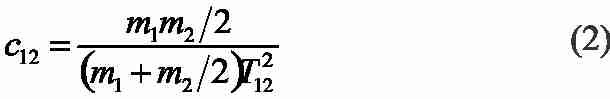
Таким образом, одним из главных вопросов при моделировании в данном случае является выбор величин сосредоточенных масс.
В результате исследований линейной модели обнаружено, что при изменении распределения массы моста между опорами и местом расположения тележки желаемая частота упругих колебаний достигается при разных амплитудах сигналов v1 и v2. Наилучшее совпадение этих амплитуд с результатами, полученными в Comsol, обеспечивается при расчете сосредоточенных масс по формулам:

где mc1,3 – сосредоточенные массы первой и второй опор соответственно, которые включают в себя массу колес, электроприводов и концевых балок, mp – распределенная масса главных балок моста, mcT – сосредоточенная масса тележки. Такое распределение масс совпадает с рекомендациями, приведенными в [2], хотя в некоторых источниках предлагается массу моста распределять равномерно между опо-рами, без средней точки [3].
Результаты моделирования линейной двухмассовой системы с рекомендуемыми параметрами приведены на рис.4, из которого видно, что полученная модель достаточно точно воспроизводит процесс перемещения конструкции, полученный в пакете Comsol Mutiphysics. На основании данной модели уже возможно синтезировать регулятор для гашения колебаний.
Одним из способов гашения упругих колебаний является применение регулятора с линейной обрат-ной связью по полному вектору состояний системы
Контур тока представляем в виде апериодического звена с постоянной времени ТT=0.01 с. Влиянием перекрестных связей для приводов переменного тока и внутренней обратной связи по ЭДС вращения двигателя пренебрегаем. Для данной системы вектор состояния имеет следующий вид:

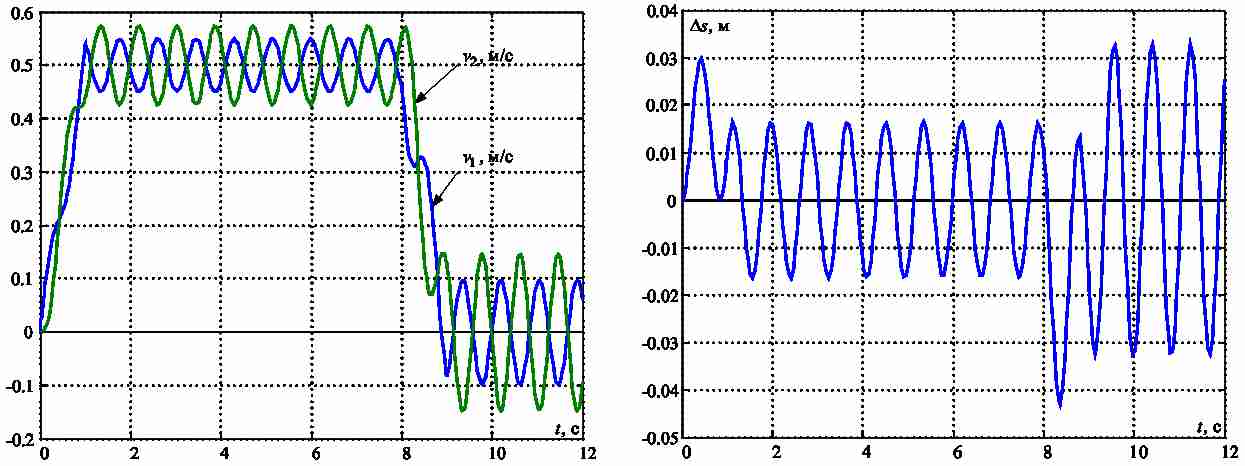
Рисунок 4 – Переходные процессы в линеаризованной системе
Коэффициенты модального регулятора рассчитываем по коэффициентам αi желаемого характеристического полинома, которые определяют динамику замкнутой системы. В результате синтеза получены следующие выражения для коэффициентов регулятора состояния:
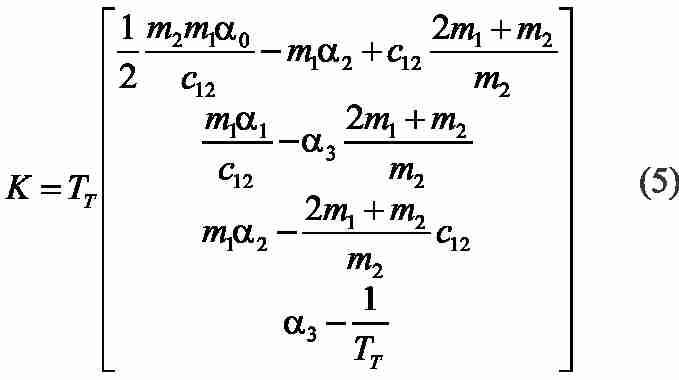
Результаты моделирования системы с таким регулятором при использовании распределения Бесселя со среднегеометрическим корнем ΩT=1/(8TT), приведены на рис.5. Видим, что колебания в системе отсутствуют, а максимальное значение отклонения средней точки моста уменьшилось по сравнению с результатами, представленными на рис.4.
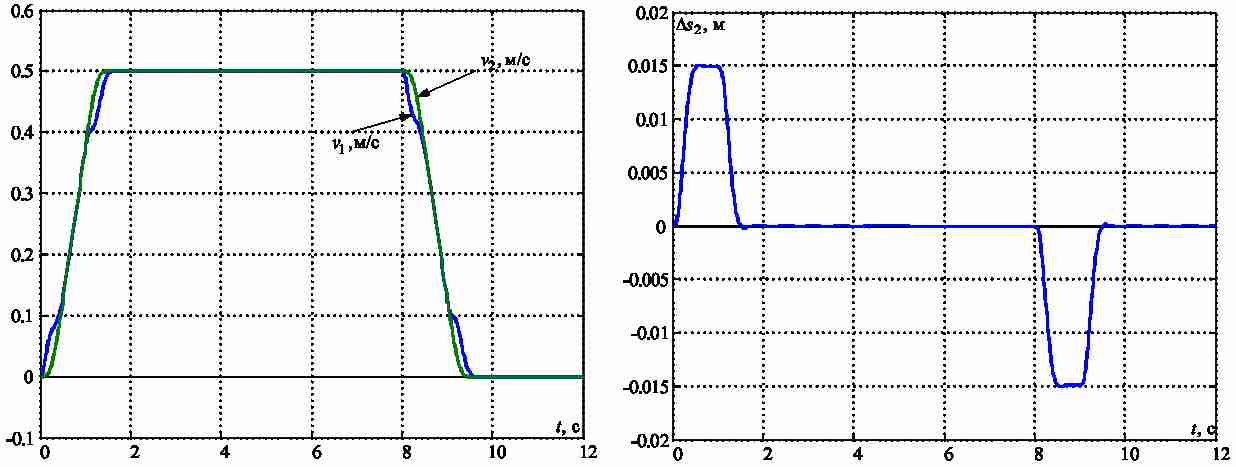
Рисунок 5 – Переходные процессы в линейной модели с регулятором состояния
Следует учитывать, что линейная модель является приближенной, а потому необходимо проверять адекватность полученных результатов на модели с распределенными параметрами.
Для этого приложим к модели моста в Comsol линейную силу, полученную в системе с модальным регулятором на выходе контура тока. Результаты моделирования представлены на рис.6.
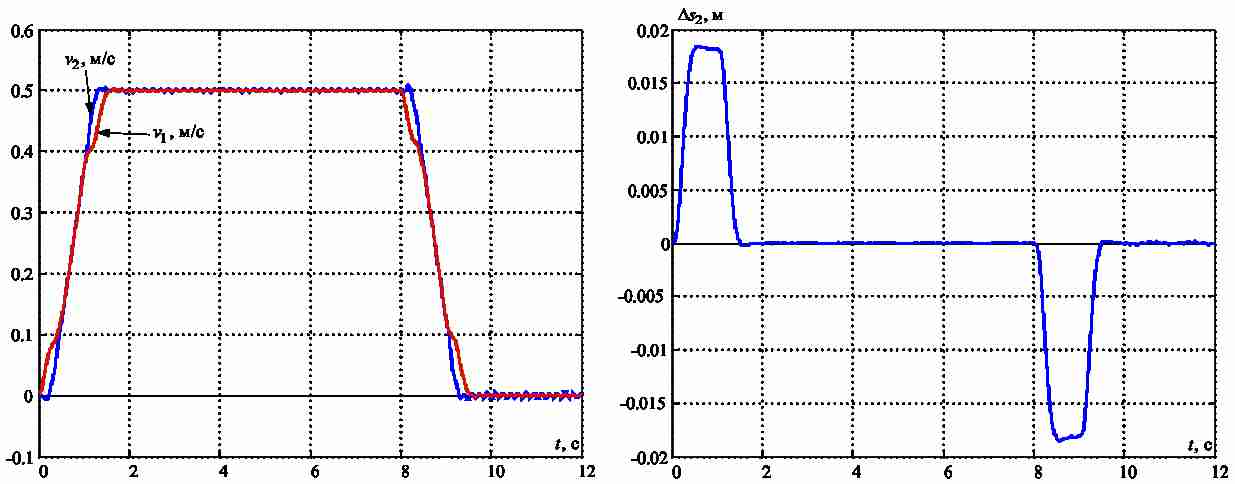
Рисунок 6 – Переходные процессы в модели с распределенными параметрами при подаче на нее выходного сигнала контура тока в системе с регулятором состояния
Видим, что низкочастотные упругие колебания полностью гасятся. При этом остаются незначи-тельные колебания более высокой частоты, не учтенные в линейной модели. Тем не менее, резуль-таты моделирования совпадают с полученными на линейной модели, что подтверждает ее адекват-ность.
Дальнейшие исследования, выполненные в Com-sol, показали, что при фиксации тележки в других точках моста характер упругих колебаний моста существенно изменяется: появляются дополнитель-ные частоты, изменяющиеся в широком диапазоне. Это делает невозможным применение синтезиро-ванного модального регулятора при большом диапазоне перемещений тележки. Для синтеза адаптивной системы управления можно использовать линейную модель моста на основании трехмассовой кинематической схемы рис.3а, в которой изменение положения тележки учитывается изменением коэффициентов упругости и распределения масс.
В этом случае перспективным представляется расчет нескольких модальных регуляторов, соответствующих различным положениям тележки, и плавный переход от одной настройки к другой при помощи нечеткого регулятора типа Сугено.
Выводы
Горизонтальное перемещение моста крана с тележкой, неподвижно закрепленной в его цен-тральной точке, можно с достаточной степенью точности описать двухмассовой системой, заменив распределенные параметры сосредоточенными в соответствии с (3). Такая модель позволяет синтезировать регулятор состояния для эффективного гашения колебаний конструкции моста в направлении его движения. Исследования следует продолжить с учетом движения тележки с подвешенным к ней грузом. Кроме того, необходимо проанализировать характер и возможность гашения вертикальных ко-лебаний, возникающих при подъеме и опускании груза.
Так же стоит отметить, что программное обеспечение имеет характеристики, которые необходимо отметить в ходе сравнения:
Список использованной литературы
1. Comsol Multiphysics User’s Guide. Version 4.2, 2011.
2. Будіков Л.Я. Багатопараметричний аналіз динаміки вантажопідйомних кранів мостового типу: Монографія. – Луганськ, вид–во СНУ ім. В.Даля, вид. 2-е, 2003. – 210 с.
3. Макурин А.В., Морозов Д.И. Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции // Електротехніч-ні та комп’ютерні системи. – 2011. – №3(79). – С. 167–169.