Аннотация
Толочко О.И., Бажутин Д.В. Анализ поперечных колебаний мостового крана при изменении положения тележки. Целью данной работы является исследование поперечных колебаний моста при разных положениях тележки как системы с распределенными параметрами с использованием пакета Comsol Multiphysics и определение параметров линейной трехмассовой механической системы с сосредоточенными параметрами, максимально точно отображающей свойства исследуемого объекта.
Мостовые краны являются дорогостоящими механическими конструкциями, для которых одной из самых актуальных задач является повышение надежности и долговечности их работы. Эти показатели в значительной мере зависят от упругих колебаний металлических конструкций.
Мостовой кран включает в себя целый ряд упругих элементов: упругий контакт колес с рельсами, упругости редукторов и передаточных механизмов, каната и непосредственно самого моста. В большинстве современных работ рассматриваются колебания конструкций моста в вертикальном направлении, которые имеют большую амплитуду. Тем не менее, упругость конструкции в горизонтальном направлении при перемещении моста даже при сравнительно небольших деформациях приводит к возникновению больших изгибающих усилий, воздействующих как на конструкцию моста, так и на его колеса, а также на элементы кинематических соединений колес с приводными двигателями. Это вызывает накопление усталости металла, возникновение механических поломок и, как следствие, приводит к снижению срока безаварийной эксплуатации механического оборудования.
Анализ колебаний моста, связанных с упругостью его конструкций, при фиксированном положении тележки может быть выполнен в пакете Comsol Multiphysics, который позволяет учитывать упругие свойства механических систем с распределенными параметрами, к которым относятся и мосты. При этом возможно получение информации о собственных частотах колебаний и деформациях в выбранных точках.
Такой анализ поперечных колебаний моста при расположении тележки в его центре выполнен в [1]. Анализ показал, что в этом случае в частотном спектре колебаний доминирует одна частота, что дало возможность приближенно представить рассматриваемый объект как двухмассовую механическую систему, в которой первая масса включает в себя массу колес моста, а вторая – массу тележки. В [1] также показано, что рассредоточенную массу моста необходимо добавить к указанным выше сосредоточенным массам колес и тележки в следующей пропорции: половина массы – к тележке и по четверти массы – к левой и правой парам колес моста, что соответствует данным, приведенным в [2]. При выбранном распределении масс легко рассчитывается коэффициент жесткости двухмассовой системы.
Иначе обстоит дело в случае, когда тележка расположена не в центре моста. При этом двигатели оказываются неравномерно загруженными, а характер деформации самого моста меняется: появляется дополнительная частота собственных колебаний, связанная со смещением тележки относительно центра моста. В этом случае целесообразным представляется использование трехмассовой механической системы в качестве приближенной модели исследуемого объекта.
Целью данной работы является исследование поперечных колебаний моста при разных положениях тележки как системы с распределенными параметрами с использованием пакета Comsol Multiphysics и определение параметров линейной трехмассовой механической системы с сосредоточенными параметрами, максимально точно отображающей свойства исследуемого объекта.
Для достижения поставленной цели исследуем механическую модель конструкции моста в программном пакете Comsol Multiphysics, представленную на рис.1.
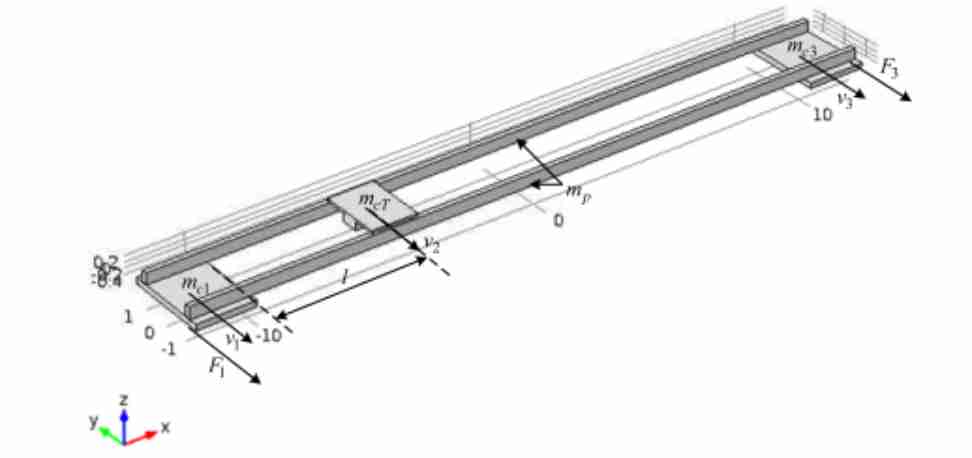
Рисунок 1 – Модель конструкции мостового крана
В ней мост представлен в виде двух балок прямоугольного сечения шириной 0.2, высотой 0.4 и длиной 20 м, масса которых m p составляет 12 т. По краям конструкции расположены две сосредоточенные массы mc1 и mc3, включающие в себя опоры, двигатели и колеса, массой 3 т каждая. Тележка имеет сосредоточенную массу mcT=2 т. Данную модель будем анализировать при разных фиксированных положениях тележки.
К крайним точкам конструкции в момент времени 0 прикладываем скачком усилие F= 5000 Н, которое снимаем также скачком через 1 с. В качестве регистрируемых сигналов используем скорости сосредоточенных масс. Результаты моделирования приведены на рис.2.
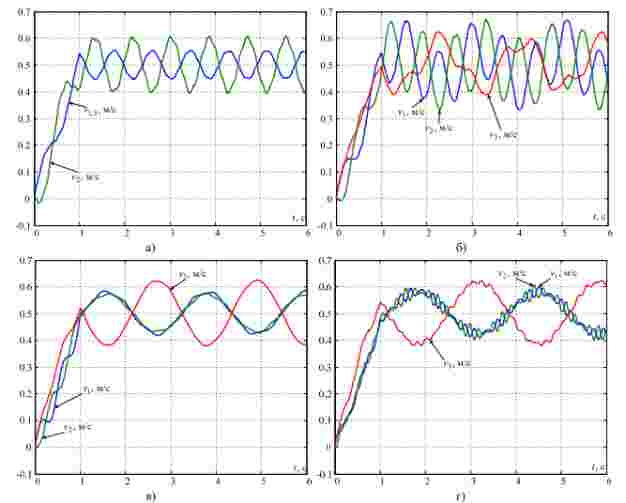
Рисунок 2 – Графики переходных процессов скоростей при различных положениях тележки l: а) 10 м; б) 8 м; в) 6 м; г) 4м
Видим, что при изменении положения тележки динамика системы существенно изменяется. Значения доминирующих частот упругих колебаний при разных положениях тележки, полученные по результатам моделирования в пакете Comsol, приведены в табл.1.
Таблица 1 – Значения частот упругих колебаний при различных положениях тележки

Следовательно, разрабатываемая трехмассовая система, используемая в качестве линейной модели иссле- дуемого объекта, должна иметь переменные параметры. Кинематическая схема такой системы приведена на рис.3. Ее математическое описание можно представить в следующем виде:
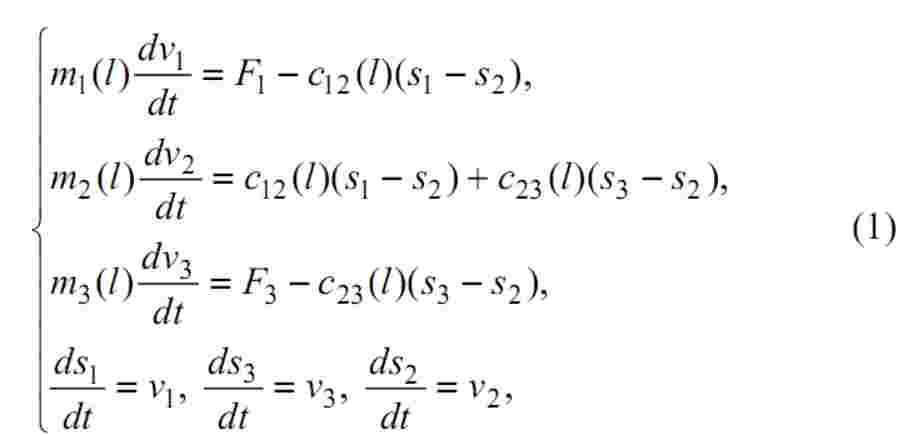
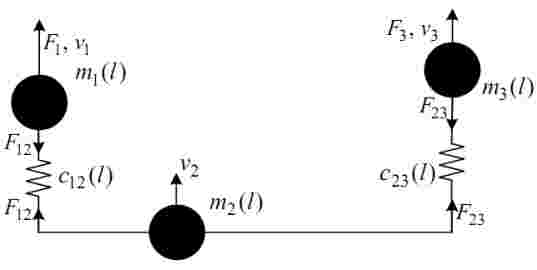
Рисунок 3 – Кинематическая схема трехмассовой системы
где сосредоточенные массы m1, m2 и m3, а также коэффициенты жесткости c12 и c23 являются некоторыми функциями положения тележки l, причем:
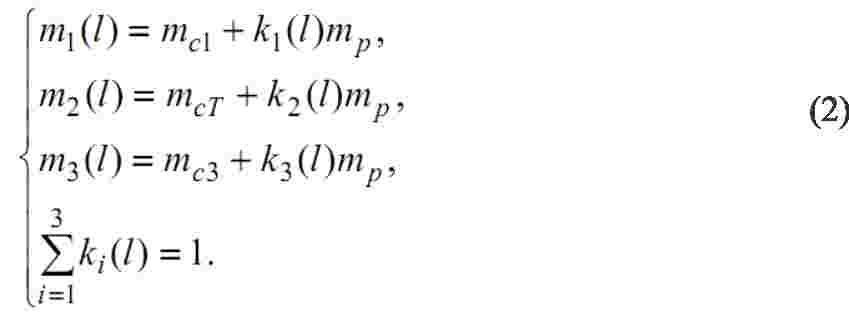
Структурная схема этой системы приведена на рис.4.
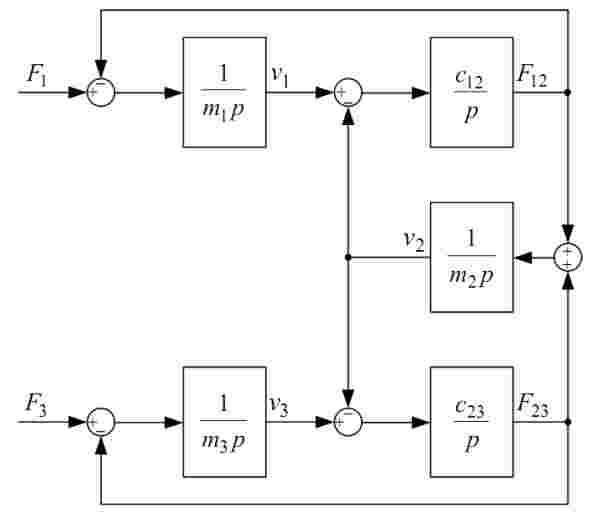
Рисунок 4 – Структурная схема трехмассовой системы
Анализируя собственные числа матрицы состояния рассматриваемой модели можно получить выражение, связывающее частоты упругих колебаний трехмассовой системы с ее параметрами:
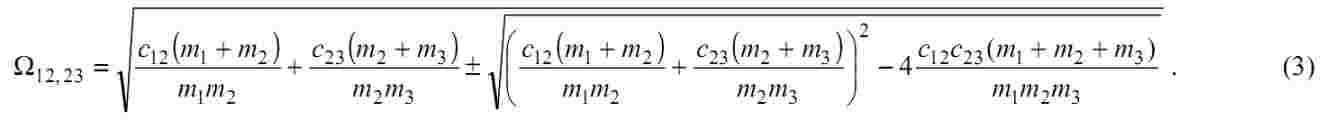
При известных значениях сосредоточенных масс коэффициенты жесткости можно определить, решая систему двух нелинейных уравнений с двумя неизвестными, полученную на основании (3).
Таким образом, имея информацию о частотах, задача идентификации линейной модели сводится к подбору значений сосредоточенных масс в соответствии с (2), так чтоб сигналы линейной модели были максимально близки к соответствующим сигналам, полученным в пакете Comsol.
На рис.5 приведены графики переходных процессов в исследуемой системе для двух положений тележки, полученные при моделировании механической модели в пакете Comsol и линейной математической модели в пакете Simulink. Из их сравнения видно, что наблюдается некоторая погрешность в амплитудах колебаний первой и второй масс, а также более выраженная вторая гармоническая составляющая в скорости третьей массы. Результаты исследований показали, что при положении тележки на расстоянии менее 4 м от края наблюдается заметное уменьшение точности линейной модели, связанное с появлением в графиках скоростей первой и второй масс дополнительных высокочастотных гармонических составляющих малой амплитуды. В этом случае возможен переход от трехмассовой к двухмассовой модели.
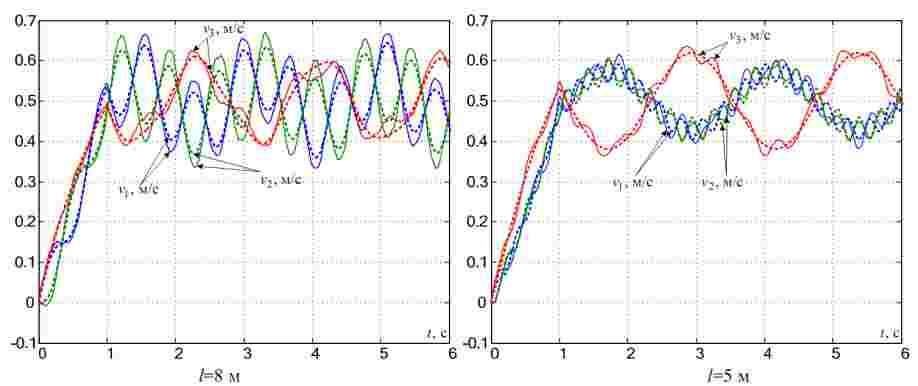
Рисунок 5 – Переходные процессы по скоростям в модели Comsol (сплошные линии) и Simulink (пунктирные линии)
На основании значений параметров, идентифицированных в дискретных точках, можно получить непрерывные графики изменения этих параметров, используя аппроксимацию полученных табличных функций степенными многочленами. Результаты аппроксимации представлены на рис.6.
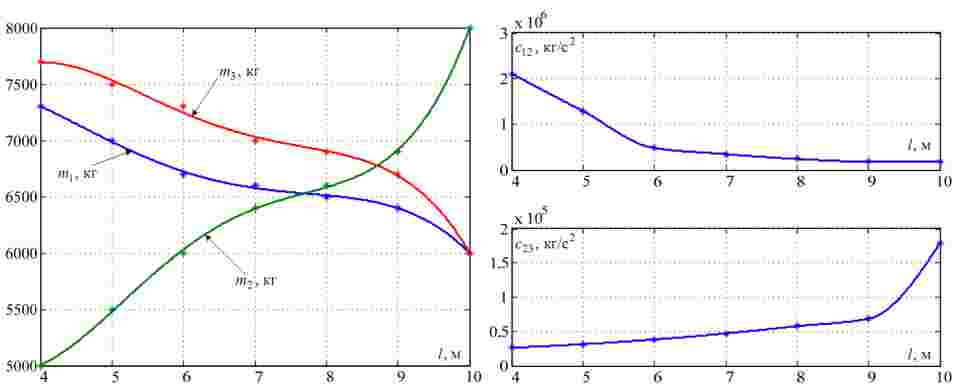
Рисунок 6 – Результаты аппроксимации зависимости параметров систем от положения тележки
На этом рисунке графики масс аппроксимированы методом наименьших квадратов полиномами 4-го порядка, а для сглаживания коэффициентов жесткости использовано интерполирование движущимися полиномами 3-го порядка. Эти графики можно использовать для адаптации системы управления.
Выводы
1. Мостовой кран с учетом упругих свойств его конструкции в поперечном направлении можно с достаточ- ной степенью точности представить в виде трехмассовой электромеханической системы, параметры которой зависят от положения тележки.
2. Разработанная линейная модель имеет удовлетворительную точность при расположении тележки на расстоянии 4 м и более от края моста и может быть использована для разработки системы управления, подавляющей упругие колебания.
Список использованной литературы
1. Толочко О.И., Бажутин Д.В., Палис Ф. Гашение горизонтальных упругих колебаний конструкции мостового крана // Електромеханічні і енергозберігаючі системи. Тематичний випуск «Проблеми автоматизованого електропривода. Теорія й практика» науково-виробничого журналу – Кременчук: КрНУ, 2012. – Вип. 3/2012 (19). – С. 336-339.
2. Будіков Л.Я. Багатопараметричний аналіз динаміки вантажопідйомних кранів мостового типу: Монографія. – Луганськ, вид-во СНУ ім. В.Даля, вид. 2-е, 2003. – 210 с.
3. Макурин А.В., Морозов Д.И. Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции // Електротехнічні та комп’ютерні системи. – 2011. – №3(79). – С. 167-169.