Анотація
Толочко О.И., Бажутин Д.В. ИОбмеження швидкості електропривода візка мостового крану при розгоні у три етапи Вісник Кременчуцького державного університету імені Михайла Остроградського – Кременчук: КДУ, 2010. – Вип. 4/2010 (63) частина 1. – С. 24-27.
Вступ
Кранові установки є невід’ємною частиною сучасного виробничого процесу, виконуючи транспортувальну функцію і пов’язуючи між собою окремі частини виробництва. Мостовий кран – установка для горизонтального переміщення вантажів, що широко використовується у металургії. Суттєвою проблемою при переміщенні вантажів за допомогою мостового крану є виникнення коливань вантажу, які погіршують енергетичні показники і надійність приводу та можуть призводити до аварійних ситуацій. Тому необхідно застосовувати додаткові засоби для гасіння цих коливань.
Аналіз попередніх досліджень.
В [1, 2] для повного гасіння коливань вантажу рекомендується застосовувати тахограми спеціальної форми (розгін та гальмування у три етапи). Однак при необхідності руху із низькою швидкістю та (або) при достатньо великих значеннях прискорення і довжини канату використання такого способу керування може привести до перевищення швидкістю на окремих ділянках розгону (гальмування) свого максимально припустимого значення. Справа у тому, що зазвичай кранові двигуни обирають з умов забезпечення бажаної усталеної швидкості руху візка, яку не слід перевищувати при гасінні коливань. Тому необхідно скоригувати запропонований закон, врахувавши обмеження на швидкість.
Мета роботи.
Вивести математичні залежності для розрахунку такого закону керування, який би забезпечив гасіння коливань вантажу без перевищення візком усталеної швидкості пересування, тобто скоригувати закон керування із врахуванням обмеження на швидкість.
Матеріал і результати досліджень.
Вивід закону керування можна здійснити на основі математичного опису, отриманого за рівнянням Лагранжа:
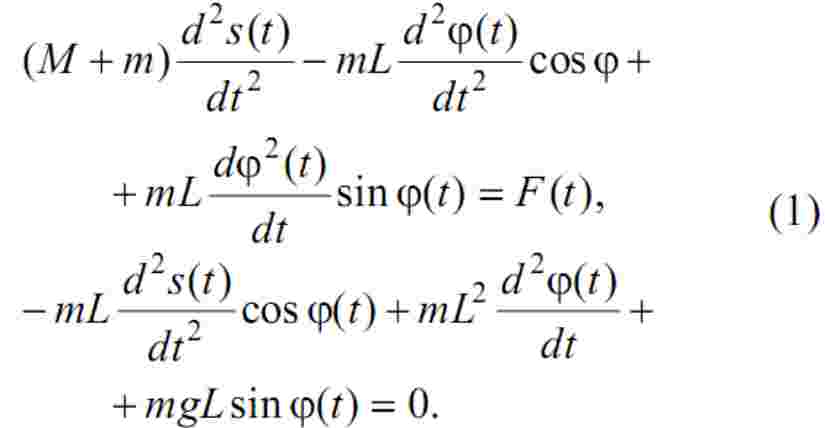
У рівняннях прийнято такі позначення: М – маса візка; F – зусилля, прикладене до візка із вантажем; m – маса вантажу; L – довжина канату; g - прискорення сил тяжіння; s – лінійне переміщення візка; φ – кут відхилення канату від вертикалі.
Враховуючи, що
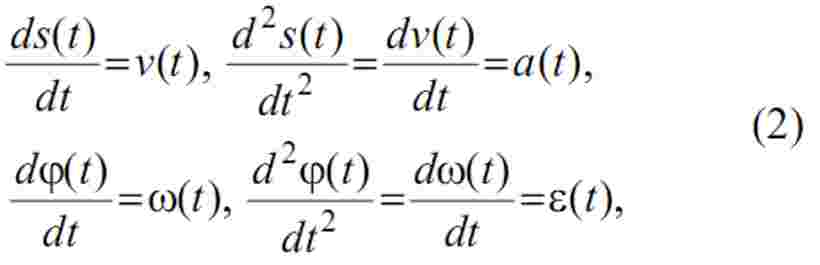
де v(t) - лінійна швидкість візка; a(t) - лінійне при- скорення візка; ω(t) - кутова швидкість коливань вантажу; ε(t) - кутове прискорення коливань вантажу; рівняння (1) можна записати у вигляді:
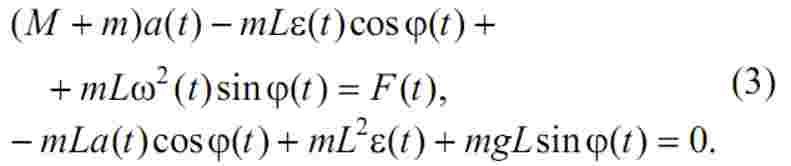
Рівняння (3) є нелінійними, що ускладнює процес оптимізації. В [1, 2] показано, що при пересуванні візка значення кута відхилення канату від вертикалі приймає досить невеликі значення, завдяки чому можна прийняти:
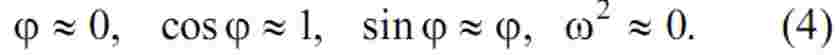
У такому випадку рівняння (3) стають лінійними:
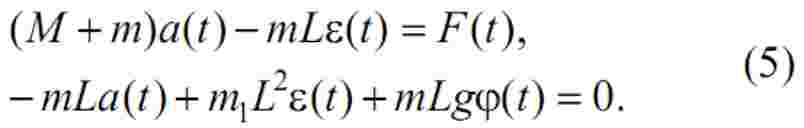
Їх можна ще більш спростити, виключивши з відповідної структурної схеми перехресні зв’язки між лінійним переміщенням візка та кутом відхилення вантажу. Таке припущення з великим ступенем точності можна робити за умови наявності системи регулювання положення візка [2]. Тоді отримаємо остаточні рівняння руху крану у такому вигляді:
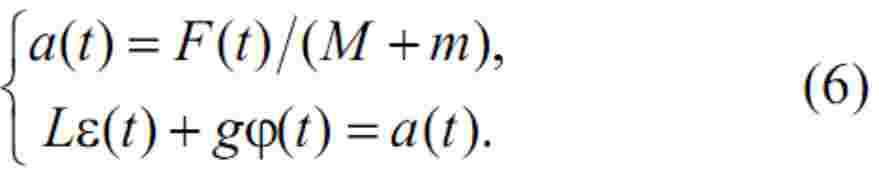
Бажаний закон керування з урахуванням обмеження швидкості у додатному напрямку складається не із 3-х, а із 4-х ділянок, як це показано на рис. 1.
Для випадку постійного значення абсолютної величини прикладеної сили на усіх ділянках розгону розв’язком рівнянь (6) будуть такі вирази для змінних стану системи:
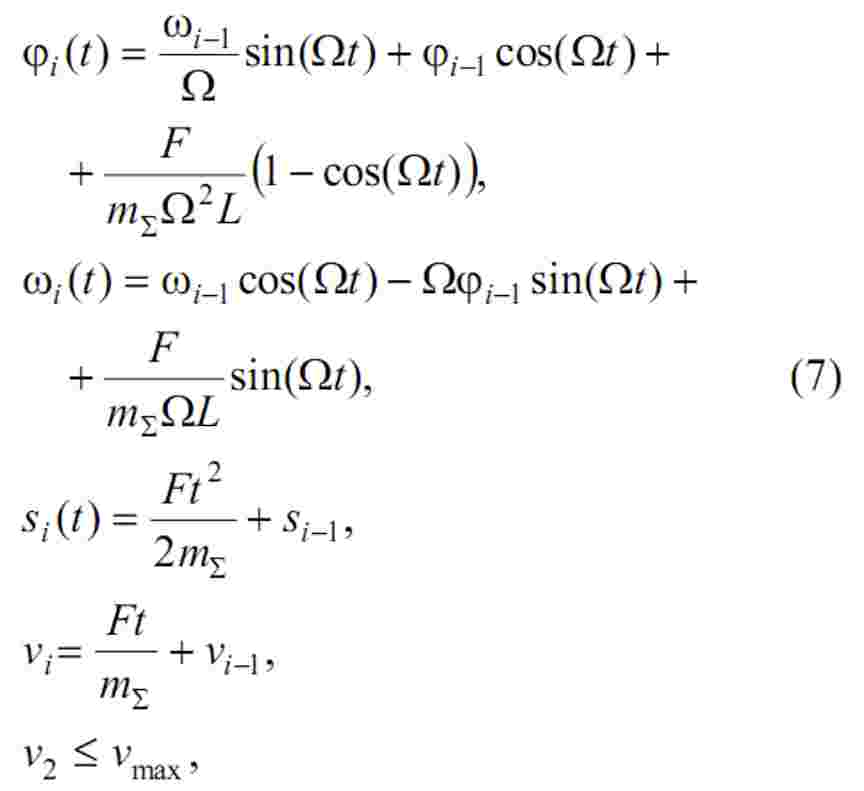
де φi, ωi,si,vi - значення змінних стану на даній ділянці розгону; φi-1, ωi-1,si-1,vi-1 – значення змінних стану в кінці попередньої ділянки розгону; Ω – кутова частота коливань вантажу.
Виведемо рівняння, що визначатимуть тривалості інтервалів розгону, гальмування та руху із усталеною швидкістю при наявності обмеження максимальної швидкості на рівні усталеної.
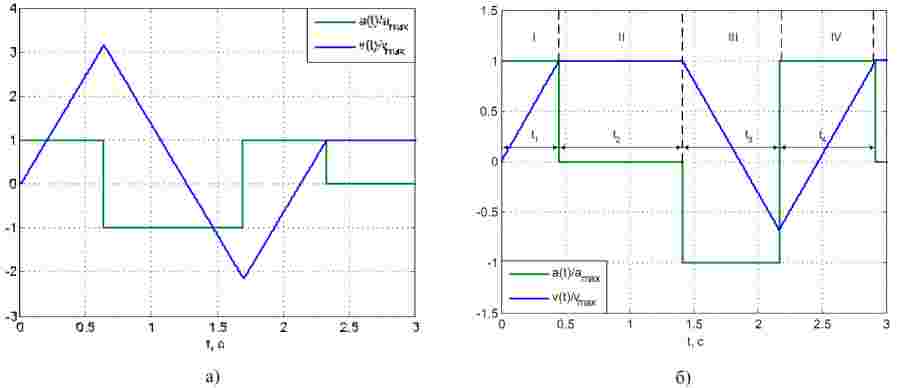
Рисунок 1 – Завдання на прискорення та швидкість візка при розгоні: а) без урахування обмеження (в 3 етапи); б) з урахуванням обмеження в додатному напрямку (в 4 етапи)
Поступово підставляючи початкові значення у рівняння (7) для кожної ділянки розгону, та після проведення усіх необхідних, перетворень отримуємо таку систему рівнянь:
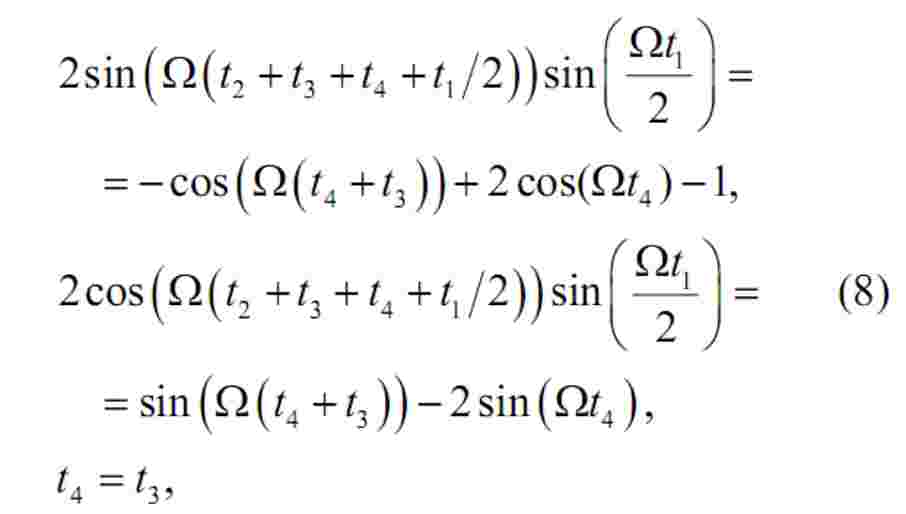
де t2, t3, t4 – невідомі тривалості інтервалів розгону, t1 – час розгону від нульової до заданої швидкості.
Така система не має аналітичного розв’язку, тому має бути розв’язана чисельними методами.
Для перевірки правильності отриманих залежностей виконаємо математичне моделювання об‘єкта регулювання, що описується рівняннями (6), без урахування інерційності системи керування при таких параметрах:
Маса візка – 500 кг; Маса вантажу – 1000 кг; Довжина канату – 15 м; Задана швидкість – 0,3 м/с; Задане прискорення – 0,66 м/с2.
Результати моделювання наведено на рис. 2. Бачимо, що коливання вантажу повністю гасяться по закінченні процесу розгону.
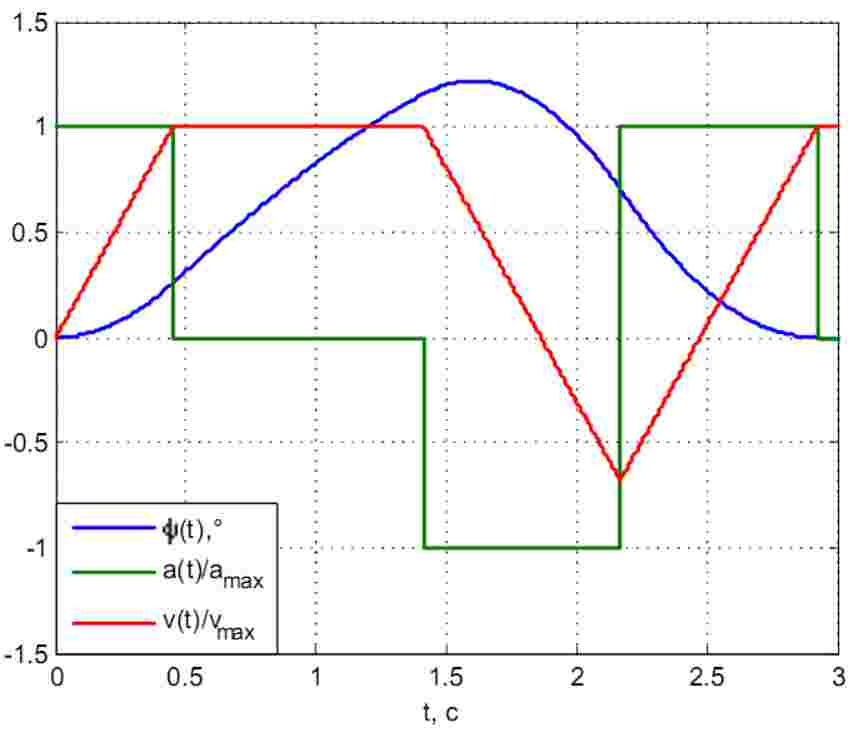
Рисунок 2 – Результати моделювання при розгоні у 4 етапи для vmax=0,3 м/с
Слід відзначити, що можливе перевищення максимального значення швидкості не тільки у додатному, але й у від‘ємному напрямку, коли швидкість змінює свій знак. Це може виникнути при ще більших значеннях довжини канату та прискорення або при дуже малому завданні на швидкість. На рис. 3 наведено результати моделювання при зменшенні максимального значення швидкості до 0,1 м/с.
Для уникнення цього необхідно ще модифікувати закон керування, ввівши обмеження на від’ємну швидкість. При цьому в законі керування з’являється додатковий інтервал руху з усталеною швидкістю, і розгін (гальмування) здійснюються в 5 етапів.
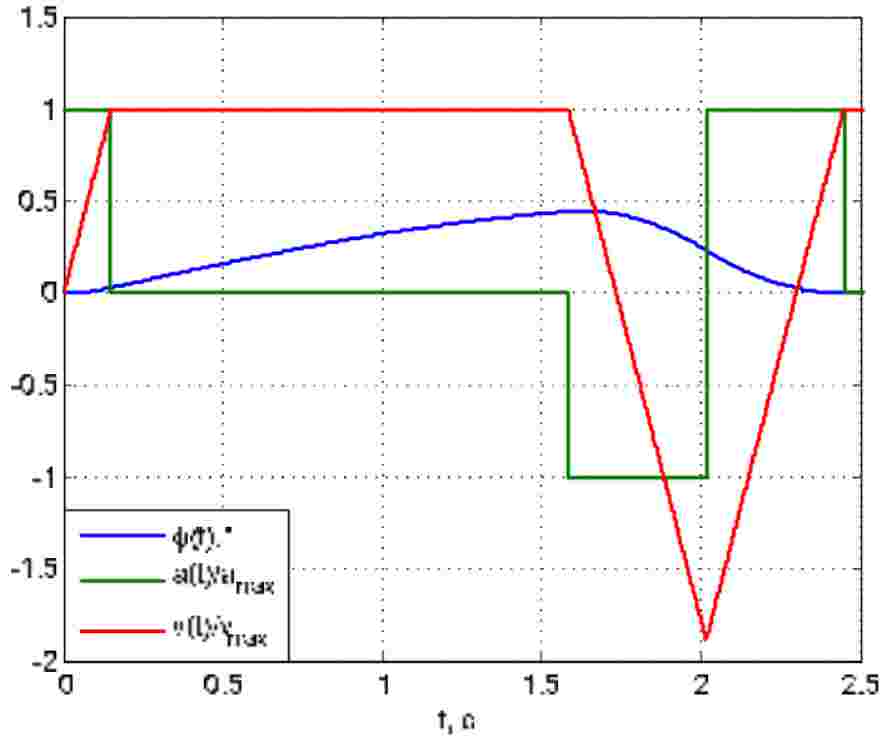
Рисунок 3 – Результати моделювання при розгоні у 4 етапи для vmax=0,1 м/с
Вивід такого закону керування виконаємо у такий же спосіб, як і для 4-етапного розгону. Після спрощень отримуємо таку систему рівнянь:

де TΣ=5t1+t2+t4- сумарний час розгону; t1 - час розгону від нульової до заданої швидкості; t2, t4 - тривалості інтервалів руху із усталеною швидкістю.
Результати такого моделювання наведено на рис.4, з якого видно, що швидкість обмежується на заданому рівні і коливання вантажу повністю гасяться по закінченні розгону.
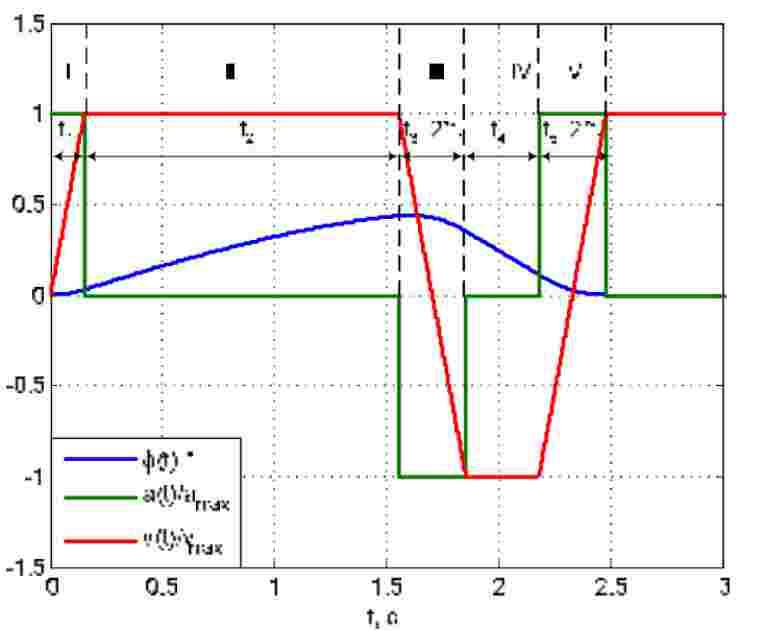
Рисунок 4 – Результати моделювання при розгоні у 5 етапів для vmax=0,1 м/с
На рис. 5 наведено графіки для прискорення, швидкості та куту відхилення вантажу при розгоні та гальмуванні у три (а) та п’ять (б) етапів. Оскільки усталене значення швидкості складає 0,1 м/с, завдання на положення було обране 1 м для покращення наочності отриманих результатів.
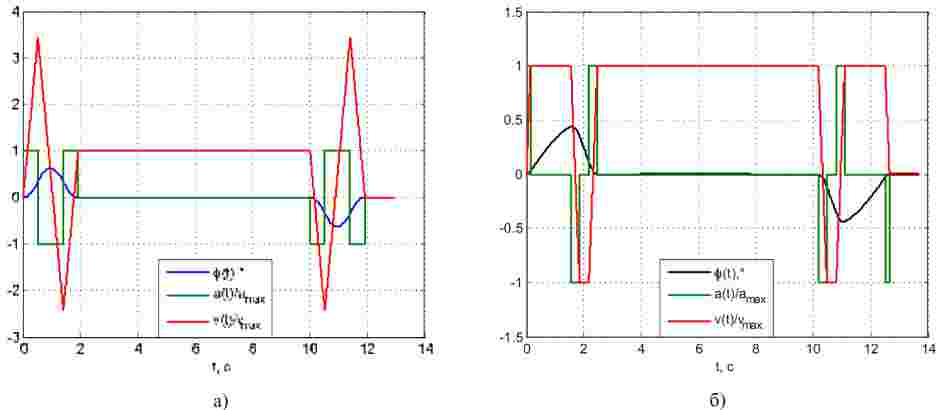
Рисунок 4 – Графіки швидкості, прискорення та кута відхилення вантажу для повного циклу позиціонування
Бачимо, що обмеження швидкості призводить до збільшення тривалості процесу позиціонування, але ця різниця складає менше 1 с, що є несуттєвим при відпрацювання досить великих переміщень.
Висновок
1. При використанні спеціальних тахограм для гасіння коливань вантажу швидкість руху може перевищувати припустимий за технологією рівень і тому має бути обмеженою. Можливе рішення – збільшення кількості інтервалів розгону та гальмування. При цьому загальна тривалість процесу позиціонування збільшується несуттєво.
2. Дослідження показали, що застосування тахограм спеціальної форми є ефективним засобом гасіння коливань лише у тих випадках, коли параметри системи (маса вантажу й візка, довжина канату) відомі із достатнім ступенем точності.
3. Неточність у визначенні мас впливає лише на значення усталеної швидкості, а тому і на точність відпрацювання положення, а неточне визначення довжини призводить до виникнення залишкових коливань вантажу, амплітуда яких змінюється приблизно у такому ж відношенні, як і довжина канату.
Причому у випадку, коли реальна довжина канату є меншою за розрахункову, амплітуда коливань, що залишаються після зупинки візка, є більшою майже у 2 рази, ніж у випадку, коли реальна довжина канату на той же процент перевищує розрахункову.
Список использованной литературы
1. Герасимяк Р. П. Анализ и синтез крановых
электромеханических систем / Герасимяк Р. П. – Одесса, СМИЛ, 2008. – 191 с.
2. A. Buch. Optimale Bewegungssteuerung von schwingungsfähigen mechatronischen Systemen mit zwei Freiheitsgraden am Beispiel eines Krans mit Pendelnder Last und elastischer Mechanik – Magdeburg,
1999. – 250 S.