Регулирование тяги с высоким использованием сил сцепления

Автор: Б. Энгель

Аннотация Б. Энгель Регулирование тяги с высоким использованием сил сцепления Статья посвящена измерению сил сцепления колеса с рельсом и колебаний для трехмассовой системы шахтного локомотива.

В 80-е годы с широким развитием тягового привода на базе асинхронных трехфазных двигателей значительно увеличилась удельная мощность локомотивов. Четырехосные электровозы серии 120 Государственных железных дорог Германии (DBAG) в настоящее время способны выполнять работу использовавшихся ранее шестиосных электровозов с коллекторными двигателями переменного тока и позволяют осуществлять рекуперативное торможение.

Эти мощные локомотивы лишь в очень редких случаях полностью используют тот максимальный крутящий момент, который обеспечивается тяговым приводом, так как слишком высокие силы тяги или торможения чреваты соответственно боксованием или юзом. Эти два нежелательных режима ведут к возникновению крутильных колебаний в тяговом тракте. Особую опасность представляют колебания силы сцепления между колесом и рельсом. Повышенное сцепление в контакте колесо - рельс в этих случаях приводит к чрезмерному износу контактирующих поверхностей. Циклический характер процесса способствует возникновению усталостных явлений в маханических элементах тягового привода. Оба фактора ведут к повышенному износу деталей и узлов тягового привода, а следовательно, к сокращению срока службы.

Последние исследования и опытные поездки показали, что вопрос использования сил сцепления все еще недостаточно изучен. Негативная роль таких явлений, как износ в тяговом тракте и особенно переменные составляющие сил на полом карданном валу, должна быть оценена в полной мере. Для активного подавления упомянутых переменных составляющих разработана новая система регулирования тягового привода.

Анализ электромеханической системы

В нижней части рис. 1 приведена кинематическая схема тягового привода с полым карданным валом электровоза серии 120. Этот тяговый тракт в проведенных ранее исследованиях моделировался как колебательная система с шестью сосредоточенными массами. На базе системного анализа она без особых потерь качества может быть преобразована в систему из трех масс.

Рис. 1. Схема замещения тягового тракта моторной оси электровоза и блок-схема системы режимного регулирования: i - вектор тока статора; u - вектор напряжения на статоре; s - сигнал управления; ASM - асинхронный трехфазный тяговый двигатель; J₁, J₂, J₃ - моменты инерции соответственно редуктора, первого и второго колес моторной оси; M_L1, M_L2 - нагрузочные моменты на первом и втором колесах (входная нагрузочная функция)

Такая система применительно к большинству современных мощных локомотивов имеет характеристические собственные формы. Первая из них с частотой 0 Гц, относящаяся к смещениям жестко закрепленных масс, здесь не рассматривается. Вторая с частотой около 20 Гц вызывает крутильные колебания колесной пары относительно ротора двигателя и скручивающие усилия на полом валу. Под действием третьей каждое из колес моторной оси колеблется относительно другого с частотой около 50 Гц. При этом крутильные колебания ротора двигателя имеют очень небольшую угловую амплитуду, в связи с чем на тяговом двигателе эту собственную форму зарегистрировать относительно трудно.

Степень гашения колебаний третьей формы в большой степени зависит от крутизны характеристики сцепления в рабочей точке для обоих колес. На рис. 2 показаны такие характеристики для разных состояний рельсов.

Рис. 2. Характеристики сцепления для разного состояния рельсов

Для сухих рельсов нестабильная область лежит справа от максимума сцепления, а стабильная слева. Дополнительное гашение колебаний колес со стороны рельсов пропорционально крутизне характеристики в рабочей точке. Это значит, что в зоне отрицательной крутизны характеристик сцепления происходит отрицательное гашение, то есть усиление колебаний и переход в нестабильную область.

Приведенные характеристики сцепления являются идеализированным приближением к реальным. Измерения показали, что реальная функция изменения сил в контакте колесо - рельс имеет стохастический характер (рис. 3).

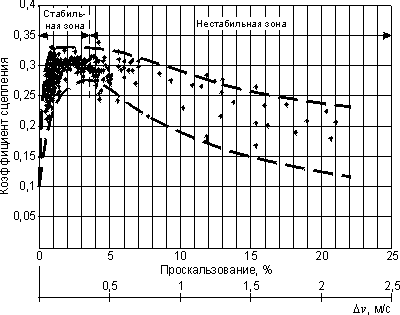
Рис. 3. Измеренные значения коэффициента сцепления

Как видно из рисунка, существует определенная полоса разброса значений, ограниченная двумя кривыми. Отчетливо видна нестабильная область. Если в ней лежит рабочая точка, то здесь возможен эффект самовозбуждения колебаний в тяговом тракте. Опыт эксплуатации показывает, насколько важно иметь достаточно большое гашение колебаний в тяговом тракте во всех рабочих областях, чтобы обеспечивался минимальный износ и исключались повреждения элементов тягового привода. Это может быть достигнуто одним из двух способов:

• использованием стабильного участка характеристик сцепления, особенно зоны II (см. рис. 2);

• активным повышением естественного гашения колебаний тягового тракта с помощью техники регулирования, например введением режимного регулирования.

Концепция регулирования

На блок-схеме рис. 1 показана возможность принципиального совмещения обоих способов снижения колебаний - их активного подавления и регулирования сил сцепления. Для этого задаваемое значение момента в магнитном зазоре M_soll формируется блоком режимного регулирования, входными величинами которого являются расчетный момент в магнитном зазоре двигателя M_r и измеренное значение угловой скорости ротора w₁. Другие параметры, вводимые в блок режимного регулирования, не измеряются, а рассчитываются в блоке оценки. Речь идет об угловых скоростях обоих колес w₂ и w₃, а также о моментах на полом валу M₁₂ и оси колесной пары M₂₃. В блок режимного регулирования вводится также задаваемое значение угловой скорости w_soll, которое в блоке логики слежения формируется на базе задаваемого значения силы тяги F_soll. С помощью воздействия на цепь регулирования частоты вращения можно активно повышать демпфирование колебаний в тяговом тракте. При этом должен охватываться весь рабочий диапазон угловых скоростей, включая самые низкие, чем обеспечивается жесткость регулирования.

Активное подавление колебаний

Поводом для исследования возможностей режимного регулирования применительно к тяговому приводу послужили результаты других исследований, проведенных Институтом электротехники при Техническом университете в Клаустале. Там была, например, разработана методика, с помощью которой для привода прокатного стана можно было определить зависимость увеличения срока службы от применяемых методов регулирования. Модель привода представляла собой колебательную систему из двух масс. Результаты исследования приведены на рис. 4, где показано относительное увеличение срока службы в зависимости от метода регулирования.

Рис. 4. Влияние метода регулирования на срок службы тягового привода

За исходный принят срок службы (L₀) системы с обычным регулированием частоты вращения. Как видно из диаграммы, наилучшие результаты получены при режимном регулировании.

В исследовании тягового привода режимное регулирование распространено на модель, представляющую собой колебательную систему из трех масс. В качестве исходных величин, определяющих состояние (или режим работы) системы, в ней использованы значения угловой скорости w₁, w₂ и w₃ трех вращающихся масс с моментами инерции J₁, J₂ и J₃, моменты на полом валу M₁₂ и оси колесной пары M₂₃, а также расчетный момент в магнитном зазоре М_r. В результате получается система 6-й степени. Векторы обратной связи формируются или заданием величины сигнала смещения, или оптимизацией квадратичной добротности колебательной системы (регулятор Риккати). Первый способ предпочтителен при самонастраивающихся режимных регуляторах. Опыт показывает, что при режимном регулировании колебательной системы из трех масс собственные формы в зависимости от используемого управляющего воздействия можно сдвигать в сторону большего гашения колебаний, чем при обычных (пропорциональных или изодромных) системах регулирования частоты вращения.

Важной проблемой при режимном регулировании является получение реальных значений всех параметров режима. На практике при использовании этого метода известными величинами являются лишь частота вращения тягового двигателя w₁ и расчетное значение магнитного момента в зазоре M_r. На рис. 5 показан расчетный блок, построенный в форме устройства слежения (система Лауэнбергера) и адаптированный к рассматриваемой колебательной системе.

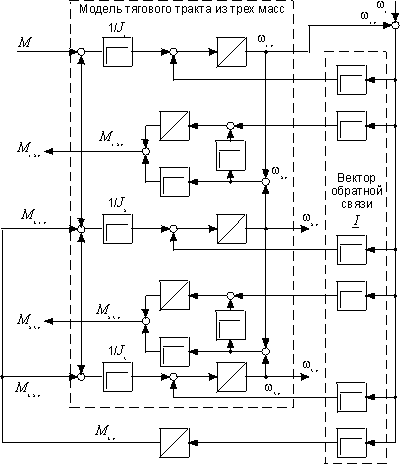
Рис. 5. Структура следящего устройства непрерывного типа для колебательной системы из трех масс: М - электромагнитный момент в зазоре; M_12r - расчетное значение момента на полом валу; M_L1r - расчетное значение нагрузочного момента на первом колесе моторной оси; M_23r - расчетное значение момента на оси колесной пары; M_L2r - расчетный нагрузочный момент на втором колесе; M_Lr - общий расчетный нагрузочный момент; w_1r - w_3r - расчетные значения угловой скорости трех масс системы

Он восстанавливает первоначальное состояние системы при возникновении отклонений параметров, сравнивая расчетное значение частоты вращения w_r с измеренным w₁ и подавая полученную разность в виде вектора обратной связи I в модель колебательной системы тягового привода.

В другом варианте схемы блок слежения Лауэнбергера заменен фильтром Кальмана, который позволяет учитывать стохастический характер процессов в контакте колесо - рельс и отстраиваться от помех при измерении параметров. Работы в этом направлении еще не завершены.

Логика системы слежения с переменным рабочим интервалом

Целью регулирования сцепления является как можно более высокое использование сил сцепления при минимальном проскальзывании колеса относительно рельса. На первый взгляд напрашивается вывод об использовании с этой целью участка с максимальным коэффициентом сцепления (зона I на рис. 2). Предположим, что такой режим задан системе логики слежения. В этом случае при стохастических изменениях состояния рельсов коэффициент сцепления может кратковременно снижаться, попадая на неустойчивый участок характеристики. За то время, пока система регулирования вновь вернется к рабочей точке с максимальным коэффициентом сцепления, в тяговом тракте может возникнуть опасный эффект самовозбуждения, который приведет к режиму движения с прерывистым сцеплением между колесом и рельсом.

Оптимальным является режим движения с рабочей точкой в зоне II (зона микропроскальзываний). Здесь при малых значениях скорости перемещения поверхности колеса относительно рельса Dv и высоком естественном гашении колебаний использование сил сцепления в контакте колесо - рельс лишь в небольшой мере хуже, чем в зоне I. Опасность неожиданного перехода в неустойчивую область здесь значительно меньше. Устанавливающийся интервал между зонами I и II зависит от дополнительного гашения колебаний, задаваемого системой режимного регулирования. В нормальных условиях естественное гашение колебаний тягового привода с помощью режимного регулирования может быть увеличено в 5 раз по сравнению с тем, которое достигается изодромным регулированием. Если сравнивать с нерегулируемой системой, то гашение будет больше в 50 раз.

Известны публикации об использовании этого метода, базирующегося на зависящей от крутизны характеристики сцепления разности между задаваемой и реальной величинами частоты вращения тягового двигателя. Ниже рассматривается аналогичный метод, но с использованием модифицированной логики системы слежения. Он наиболее приемлем для характеристик сцепления без явно выраженных максимумов, как на кривой для влажных рельсов на рис. 2.

Использовавшиеся ранее системы слежения не могли обеспечить работу тягового привода в оптимальном режиме (зона II), так как они играли вспомогательную роль. Система слежения должна обеспечивать устойчивое положение рабочей точки на характеристике сцепления. Это может быть достигнуто при режимном регулировании моторных осей. Важно, чтобы логика слежения не использовала результатов измерения скорости подвижного состава относительно пути. В поездах с концевыми моторными вагонами (например, ICE) для измерения скорости служат немоторные оси промежуточных вагонов. В мощных локомотивах этой возможности нет, так как все колесные пары используются для тяги. Здесь остается лишь возможность применения радара для измерения поступательной скорости. В то же время из рис. 2 видно, что оптимальная величина Dv для разных состояний рельсов различна.

Логика системы слежения предназначена для регулирования всего тягового тракта. Основной входной величиной является задаваемое значение силы тяги F_soll, которое вводит машинист или автоматическая система регулирования тяги и торможения (ABF). Выходная величина логики слежения - задаваемое значение ускорения a_soll, путем интегрирования которого формируется задаваемое значение угловой скорости для электрических приводов с регулированием частоты вращения. При режимном регулировании входными параметрами логики слежения являются задаваемое значение вращающего момента М_soll и его производная по времени. Вместо М_soll может также использоваться расчетный магнитный момент М_r, так как в современных приводах они различаются незначительно.

Новым в рассматриваемом методе является также применение производной по времени для формирования верхней точки переключения P_max (см. рис. 2). В соответствии с характеристикой при увеличении разности скоростей Dv темп увеличения силы тяги и соответственно момента М_soll должен непрерывно снижаться. Это значит, что в точке максимума сцепления производная момента М_soll будет равна нулю, если пренебречь ускорением вращающихся масс, т. е. принять, что боксования не будет. С помощью величины P_max может задаваться минимальный темп увеличения вращающего момента, при этом a_min < a_soll < a_max. Таким образом, назначение логики системы слежения состоит в том, чтобы обеспечивалось условие: проскальзывание колес или увеличение разности скоростей Dv может быть допущено лишь в том случае, если это оправдано необходимостью увеличения силы тяги.

Помимо этого планируется в системе режимного регулирования задавать параметры P_max и P_min через так называемый показатель использования сцепления с учетом износа (AG). С его помощью система определяет приоритетность повышения степени использования сил сцепления или предотвращения повышенного проскальзывания колес. Если задать AG = 100 %, это приведет к режиму тяги на пределе сцепления с относительно высоким проскальзыванием колес. В нормальной эксплуатации показатель AG должен быть значительно ниже. Тем самым будет обеспечено снижение износа колес, а значит, и затрат на техническое обслуживание, и капиталовложений за счет увеличения срока службы всех элементов тягового тракта.

Стенд для моделирования регулирующих систем тягового привода

Для испытаний и оптимизации новых систем регулирования тягового привода существует несколько возможностей:

• цифровое моделирование всей системы тягового привода;
• проверка аппаратного и программного обеспечения путем аналогового или цифрового моделирования испытательных участков в реальном времени;
• использование испытательных стендов и полигонов;
• испытания отдельных компонентов или единиц подвижного состава в целом на катковых или нагрузочных стендах;
• опытные поездки на линии.

В Институте электротехники разработан новый метод, основанный на использовании стенда, на котором масштабно моделируется динамика всего механического тракта в системе тягового привода электровоза серии 120. Как уже сказано, тракт тягового привода мощного электровоза может быть смоделирован как колебательная система из трех масс. Структура стенда основана на этом принципе, причем здесь могут быть реализованы собственные частоты крутильных колебаний 20 и 50 Гц. Для повышения точности моделирования и сравнимости результатов задаваемые на стенде параметры, а именно угол скручивания, частота вращения и угловые ускорения, принимаются такими же, как на локомотиве. В связи с этим одноступенчатый редуктор с цилиндрическими шестернями и таким же, как на локомотиве, передаточным числом, равным 5,067, является важнейшей составной частью стенда.

Динамика стенда должна отвечать всем требованиям, которые вытекают из закона подобия, применяемого в механике. Это достигается тем, что моменты инерции, жесткость пружин, константы гашения колебаний и внешние моменты, действующие на локомотиве, должны быть уменьшены на стенде в одном масштабе. В данном случае используемое оборудование стенда определило масштаб уменьшения параметров 1:100. Колебательная система, состоящая из электрической машины, моделирующей тяговый двигатель, и двух нагрузочных трехфазных машин, соединенных валом и моделирующих два колеса моторной оси, на стенде дополнена электромагнитными моделями двух контактов колесо - рельс. Эти модели воздействуют на поле в магнитном зазоре одной из нагрузочных электрических машин. Рассматриваемый стенд отличается от всех других тем, что здесь используется упомянутый закон механики о подобии.

В основу стенда положено исследование тяговых приводов с индивидуальным регулированием осей. На нем могут испытываться и сравниваться следующие концепции регулирования:

• комплексное регулирование силы сцепления;
• различные логические схемы слежения;
• методы регулирования частоты вращения;
• режимное регулирование с активным подавлением колебаний;
• расчет и оценка механических режимных параметров;
• определение срока службы компонентов тягового привода.

Системы регулирования тягового привода исследуются с помощью устройства ASG, являющегося оригинальной разработкой.

Преимущество стендовых испытаний перед натурными заключается в том, что стенд приспособлен для исследования экстремальных динамических нагрузок и оборудован защитными муфтами. Благодаря этому возможны испытания с рабочими точками, расположенными на неустойчивых участках характеристики сцепления, и новыми системами регулирования. При этом отсутствуют ограничения, связанные с опасностью повреждения компонентов тягового тракта.

Другое преимущество заключается в том, что при испытаниях воспроизводимы все режимы.

Концепцией стенда, основу которого составляют три электрические машины, определяется число масс в модели колебательной системы, равное трем.

Тяговый привод стенда состоит из асинхронного двигателя мощностью 18,5 кВт с короткозамкнутым ротором и преобразователя с промежуточным звеном постоянного напряжения мощностью 25 кВ·А. Постоянная времени регулирования частоты вращения равна 5 мс. Номинальные режимы стенда в соответствии с масштабом уменьшения 1:100 следующие: мощность 14 кВт, вращающий момент 75 Нм, момент при трогании 105 Нм. Параметрами стенда они обеспечиваются с большим запасом.

Обе нагрузочные машины мощностью по 30 кВт моделируют инерцию масс двух колес моторной оси. С помощью собственных преобразователей в них формируются нагрузочные моменты на базе электромагнитных моделей контакта колесо - рельс. Нагрузочные машины и их преобразователи имеют достаточную мощность для моделирования любых режимов. Так, каждый из нагрузочных приводов в состоянии противостоять вращающему моменту, передаваемому редуктором от тягового двигателя, что соответствует полной разгрузке колеса. Динамика их вращающего момента такова, что позволяет оптимально моделировать характеристику сцепления.

Модель контакта колесо - рельс упрощенно можно охарактеризовать как модель поезда в сочетании с характеристикой сцепления. В модели поезда сила тяги, которая пропорциональна нагружающему моменту, интегрируется по скорости, причем масса поезда является постоянной интегрирования.

Еще одним преимуществом стенда перед измерительными поездками локомотива является простота подключения измерительных датчиков в тракте тягового привода. Так, каждая из трех вращающихся масс стенда оснащена оптическим датчиком приращений частоты вращения. Между этими вращающимися массами находятся два вала, изготовленные с высокой точностью и предназначенные для измерения вращающего момента. С их помощью измеряются вращающие моменты полого вала М₁₂ и оси колесной пары М₂₃. Благодаря этому возможно изучение динамики колебательной системы. Однако пока в соответствии с концепцией эти измеряемые величины не используются в качестве входных величин устройства, регулирующего частоту вращения тягового двигателя, а служат лишь для проверки точности расчетных величин.

Точное моделирование тягового тракта по результатам его расчета и техническим характеристикам, гарантированным изготовителем, приводит к модели колебательной системы из 19 масс. Упрощение модели на базе имеющихся научных разработок в области сокращения до минимума числа дискретных колебательных компонентов в сложных колебательных системах позволяет получить модель с тремя или двумя массами. Если сравнить распределение собственных форм этих двух систем с моделью реального тягового тракта, состоящей из трех масс, можно обнаружить достаточно точное совпадение в отношении собственных колебательных форм. Оказывается, что вторая собственная форма соответствует частоте 20 Гц, а ее гашение имеет ту же величину, что и в реальном тяговом приводе. Третья собственная форма 50 Гц имеет в модели большее гашение, чем в оригинале. Это объясняется тем, что в системах меньшей мощности степень гашения выше.

Результаты стендовых испытаний

На рис. 6 показано поведение тягового привода при использовании нового режимного (а) и обычного (б) изодромных регуляторов при изменении условий тяги.

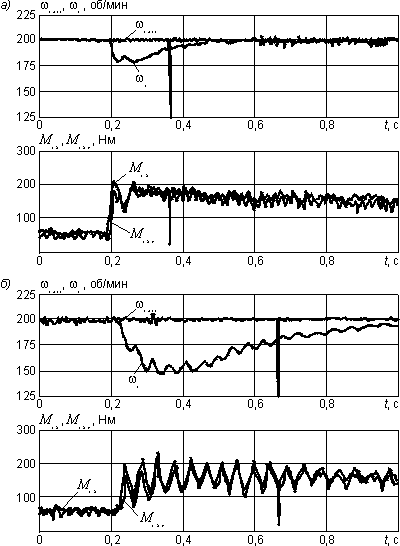
Рис. 6. Действие системы режимного регулирования (а) в сравнении с обычной изодромной системой (б) при изменении нагрузки

В обоих случаях в момент времени t = 0,2 c на второй нагрузочной машине (колесо с непрямым приводом) реализовано скачкообразное увеличение нагрузочного момента с 50 до 150 Нм. Для анализа состояния использованы значения частоты вращения тягового двигателя w₁, задаваемого значения частоты вращения w_soll, а также расчетное и измеренное значения момента полого вала соответственно М_12r и М₁₂. Полученные результаты показали, что обычный изодромный регулятор не смог погасить крутильные колебания в модели полого вала с частотой 20 Гц, а в случае использования режимного регулятора эти колебания оказались погашенными. В системе с режимным регулятором снижение частоты вращения, а также время возврата в нормальный режим значительно меньше, а диапазон регулирования в 7 раз больше, чем с обычным изодромным.

В то же время система расчета момента на полом валу в обоих случаях была достаточно точной, что было видно из сравнения моментов М_{12 r} и М₁₂.

На рис. 7 показана работа стенда с обычным изодромным регулятором без активного гашения колебаний. В тяговом режиме при скорости поезда 10 м/с и 90 % задаваемого значения вращающего момента в момент времени t = 0,2 c коэффициент сцепления скачкообразно падает со 100 до 60 %.

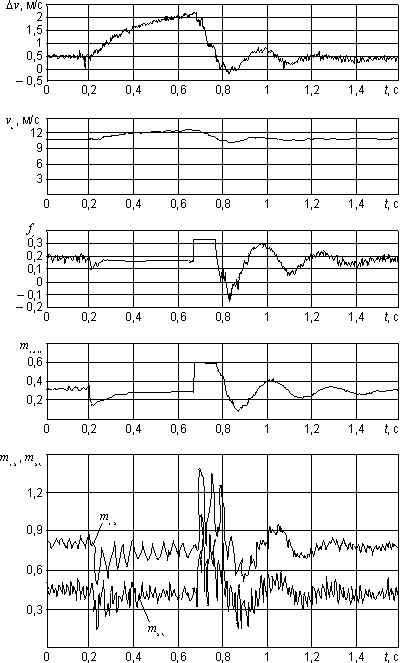
Рис. 7. Действие обычной изодромной системы регулирования при изменении условий сцепления: v_u - окружная скорость колеса; f_x - коэффициент сцепления в продольном направлении; m_soll - приведенный задаваемый момент, используемый при формировании модели силы сцепления; m₁₂, m₂₃ - приведенные моменты полого вала и оси колесной пары

Как известно из практики, возникают интенсивные колебания моментов М₁₂ и М₂₃. Действующая сила сцепления слишком мала для того, чтобы вернуть тяговый тракт на устойчивый участок характеристики сцепления. В результате возникает боксование, что видно по увеличению разности скоростей Dv. В результате последующего увеличения коэффициента сцепления вновь возникают значительные колебания моментов М₁₂ и М₂₃. Помимо собственных форм с частотами 20 и 50 Гц отчетливо видна затухающая частота 5 Гц. Она генерируется регулирующей цепью при моделировании на стенде коэффициента сцепления.

На рис. 8 приведены результаты моделирования процесса трогания с использованием современной (режимной) концепции регулирования.

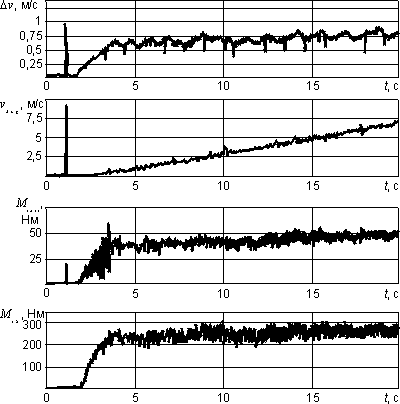
Рис. 8. Действие системы режимного регулирования при трогании поезда: v_Zug - скорость поезда

Задаваемое значение силы тяги принято максимальным, равным 300 кН. Из кривой изменения разности скоростей Dv видно, что в среднем она остается равной 0,75 м/с, то есть значительно ниже величины 1 м/с, соответствующей максимуму сцепления. Это значит, что рабочая точка находится на устойчивом участке характеристики. Частота, с которой логика слежения в процессе регулирования оказывает управляющее воздействие на параметры, составляет 0,7 Гц. Несмотря на это, увеличение скорости поезда происходит равномерно, почти линейно, что объясняется его большой массой. Величины Dv и v_Zug определяются нагрузочной компонентой моделей поезда и контакта колесо - рельс. В кривой изменения момента полого вала М₁₂, как и ожидали исследователи, влияния колебаний первой собственной формы не было обнаружено. Рассмотренные результаты показали, что новая система регулирования с активным гашением колебаний достаточно эффективна.

Перспективы

Работы по данной теме будут продолжены с целью совершенствования блока расчета в модели путем введения предварительной обработки характеристик и/или включения в него фильтра Кальмана для обработки входных нагрузочных функций, имеющих стохастический характер. По окончании стендовых исследований планируется проверка результатов моделирования на электровозе высокой мощности.