В настоящее время актуальной является разработка математической модели электрической станции, позволяющей анализировать переходные процессы, возникающие при однофазных и многофазных коротких замыканиях [КЗ] в отходящих линиях электропередач, на сборных шинах, в трансформаторах, а также при неполнофазных отключениях выключателей высокого напряжения, обрывах фаз и др.
Для создания такого класса математической модели требуются полные математические описания всех элементов главной схемы электрических соединений электрической станции на основе полных дифференциальных уравнений.
Уравнения для элементов, обладающих пофазной симметрией (ЛЭП, трансформатор, кабель), записываются в трёхфазной системе координат a, b, c или в двухфазной системе х, y, то есть в неподвижной относительно статоров генераторов. Для симметричных электрических машин (асинхронные двигатели) используются оси х, y, а для несимметричных (синхронные генераторы и двигатели) – система координат, жёстко связанная с осями d, q ротора. При этом на каждом шаге расчёта для синхронных машин осуществляется пересчёт режимных параметров от осей d, q к осям всех остальных элементов a, b, c или х, y.
В соответствии с заданной схемой соединений записываются уравнения связи между элементами, с помощью которых определяются узловые напряжения в схеме, а затем решаются дифференциальные уравнения отдельных агрегатов сети.
При использовании математических моделей многомашинных систем, описанных полными дифференциальными уравнениями, часто возникают трудности с получением устойчивости решения, а также с формированием модели всей системы. Поэтому основной алгоритм расчёта переходных процессов выполнен на основе дискретной модели, которая позволяет получать пошаговые решения из схемы для стационарного режима. Схема составляется с применением к исходным дифференциальным уравнениям одного из неявных методов численного интегрирования.
В моделях вращающихся электрических машин (двигатели и генераторы) используются схемы замещения с многоконтурным ротором , что позволяет более точно учитывать эффект вытеснения тока в роторе.
С помощью данной модели производится расчёт мгновенных значений токов короткого замыкания, оценивается поведение генераторов при КЗ различной удалённости, поведение асинхронных и синхронных двигателей на секциях собственных нужд, а также может быть выполнен анализ асинхронных режимов турбогенераторов, возникающих при потере возбуждения. Представляется возможным определять предельное время допустимой длительности КЗ из условия обеспечения динамической устойчивости синхронных генераторов и с учётом получаемых результатов осуществлять выбор уставок устройств релейной защиты и противоаварийной автоматики. Модель реализована на языке Microsoft® Visual C++ 7.NET применительно к современным ПЭВМ, работающим под управлением операционной системы Microsoft® Windows и является основой программного продукта под названием PowerNet.
На рисунке 1 показана копия экрана с участком программы (рабочее окно «Осциллограф»), на котором представлено изменение кривых тока статора АД типа 4А -20 и напряжения на секции 0,4 кВ в переходном режиме по схеме пуск – нормальная работа – КЗ - ликвидация КЗ – восстановление питания – самозапуск.
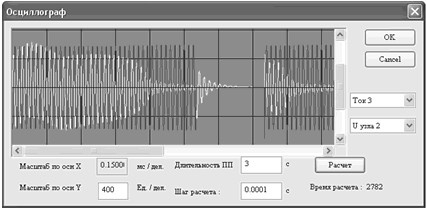
Рисунок 1 – Кривые тока статора (белый цвет) АД и напряжения на секции 0,4 кВ (чёрный) в переходном процессе