Аннотоция
Онищенко В. П., Кузавка А. В. К вопросу о расчёте витков резьбы на изгибную прочность Обычно расчет витков резьбы на прочность производится на срез основания витка и смятие его контактной поверхности. Расчёт на изгибную прочность витков резьбы представляет собою весьма сложную, статически неопределимую задачу. И поэтому отношение к этому виду расчета не однозначно. Например, Павлов Я. М. [1] считает, что наиболее опасной (по сравнению со срезом и смятием) является изгибная деформация витков, тогда как Решетов Д. Н. [2] рекомендует вообще не рассчитывать витки резьбы на изгибную прочность из-за большой условности принятых расчетных моделей.
Цель работы
Целью работы является оценка необходимости расчета витков резьбы на изгибную прочность на основе анализа результатов определения нормальных напряжений с помощью трех расчетных моделей витка:
- модель в виде консольной балки;
- модель в виде круглой пластинки;
- метод конечных элементов.
Ход работы
Исследования проводились на группе болтов разного диаметра с квадратным профилем витка. Параметры квадратной резьбы приняты на основе ГОСТ 24737-81 на однозаходную трапецеидальную резьбу.
Нагрузка на болт F определялась из условия работы стержня на растяжение при допускаемых напряжениях равных [σ] = 100 МПа
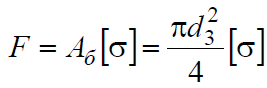
где Aб – площадь поперечного сечения стержня болта,
d3 – внутренний диаметр стержня болта.
Как показал Н. Е. Жуковский [3], нагрузка по виткам резьбы распределяется неравномерно. При десяти витках на первый виток приходится 34% полной нагрузки, тогда как на десятый виток приходится около 1% общей нагрузки. В связи с этим, расчет витка на изгибную прочность производился по силе
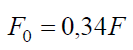
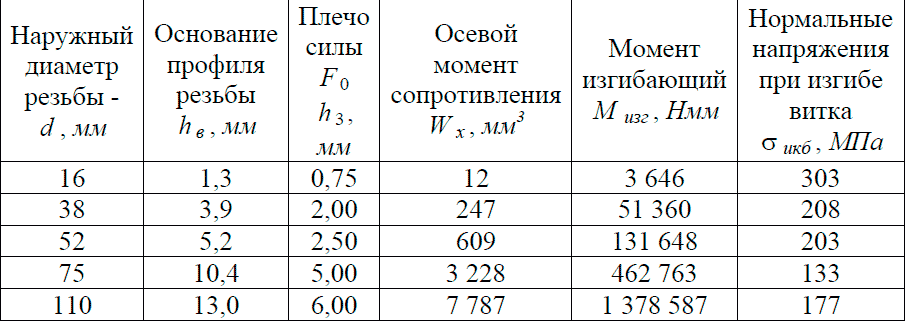
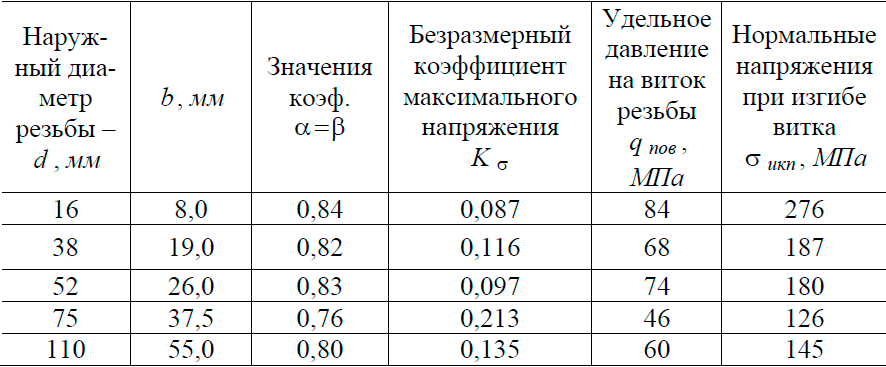
Принято допущение, что болт и гайка изготовлены из одного и того же материала. Поэтому рассчитывались на изгибную прочность витки болта. Исходные данные для проведения исследования представлены в табл. 1.
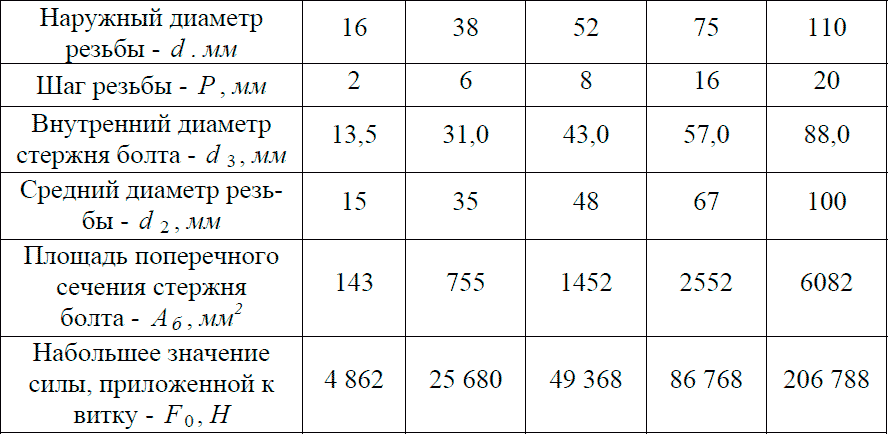
Таблица 1 – Исходные данные для расчета витков болтов на изгибную прочность
Модель витка в виде консольной балки
Модель образована разверткой основания витка резьбы болта, закрепления его на плоскости и нагружения силой Fо, распределенной по среднему диаметру с интенсивностью q = F0 / π*d3 (рис. 1).
С целью упрощения задачи трапецеидальный профиль заменен прямоугольным профилем, одна сторона которого равна ширине основания трапецеидального профиля – hв = 0,65 * P [4], а другая сторона равна высоте этого профиля – Н = (d-d3) / 2.
Нормальные напряжения при изгибе консольной балки определяются по формуле
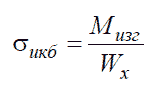
где Мизг = F0 * h3 = F0 * (d2-d3) / 2 – момент изгибающий,
Wx – осевой момент сопротивления основания балки.
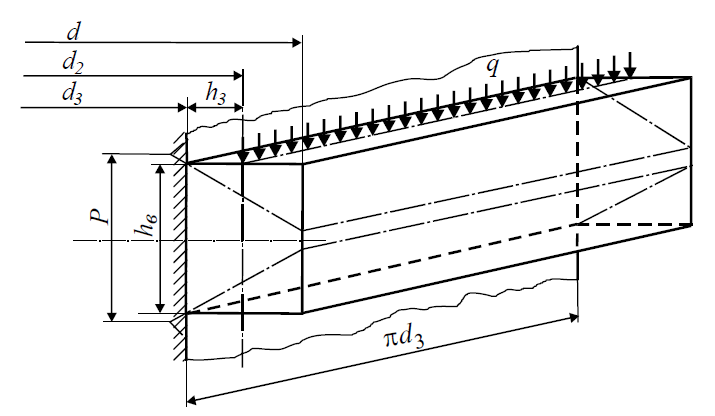
Рисунок 1 – Расчетная модель витка резьбы в форме консольной балки
Таблица 2 – Результаты определения напряжений при изгибе витка резьбы, смоделированного в виде консольной балки
Модель витка в виде консольной балки
Модель (рис. 2) представляет собой круглую пластинку жесткозакрепленную на стержне диааметром d3 и имеющую поперечное сечение, равное сечению витка резьбы смоделированного в виде консольной балки.
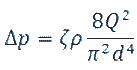
Рисунок 2 – Расчетная модель витка резьбы в виде круглой пластинки
Определение нормальных напряжений при изгибе круглой пластинки, нагруженной удельным давлением q, производится по формулам и таблицам, приведенным в работе [5].
Нормальные напряжения вычисляются в месте закрепления пластинки ( di = d3 ) приняв допущение, что dc = d3, по формуле
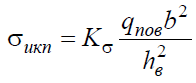
Таблица 3 – Результаты определения напряжений при изгибе витка резьбы, смоделированного в виде круглой пластинки
Моделирование витка резьбы методом конечных элементов
Метод конечных элементов (МКЭ) является наиболее перспективным численным методом, что позволяет осуществлять анализ напряженнодеформированного состояния любой конструкции [6].
Для решения задачи использовалась система APM WinMachine, одиниз модулей которой – APM Beam использовался для анализа напряженнодеформированного состояния исследуемого объекта.
APM Beam – модуль проектирования балочных элементов конструкций. Модуль предназначен для выполнения комплексного проверочного расчета балки в условиях произвольного нагружения и закрепления. Балка может состоять из нескольких участков разной длины с различными поперечными сечениями. С помощью APM Beam можно получить следующие результаты:
- реакции в опорах балки;
- распределение моментов и углов изгиба по длине балки;
- распределение моментов и углов поворота при кручении;
- расчет поперечных и продольных деформаций;
- распределение эквивалентных напряжений по длине балки;
- распределение поперечных сил;
- карты распределения напряжений в любом произвольном сечении по длине балки;
- частоты собственных колебаний.
В качестве расчетной принята модель витка резьбы в виде круглой пластинки (рис. 2). На базе этой модели была создана объемная 3D модель исследуемого объекта, которая была разбита на конечно-элементную сетку (рис. 3). После нагружения объемной модели витка резьбы уровень напряжений каждого элемента выделяется определенным цветом. Пример результата исследования напряженного витка резьбы методом МКЭ представлен на рис. 4.

Рисунок 3 – Пример разбивки витка резьбы на конечно-элементную сетку

Рисунок 4 – Пример исследования напряженного состояния витка резьбы методом МКЭ
Таблица 4 – Результаты определения напряжений при изгибе витка резьбы, найденных методом конечных элементов
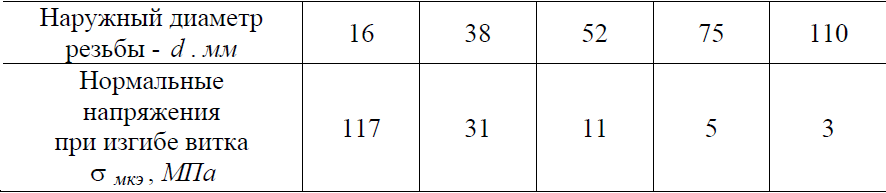
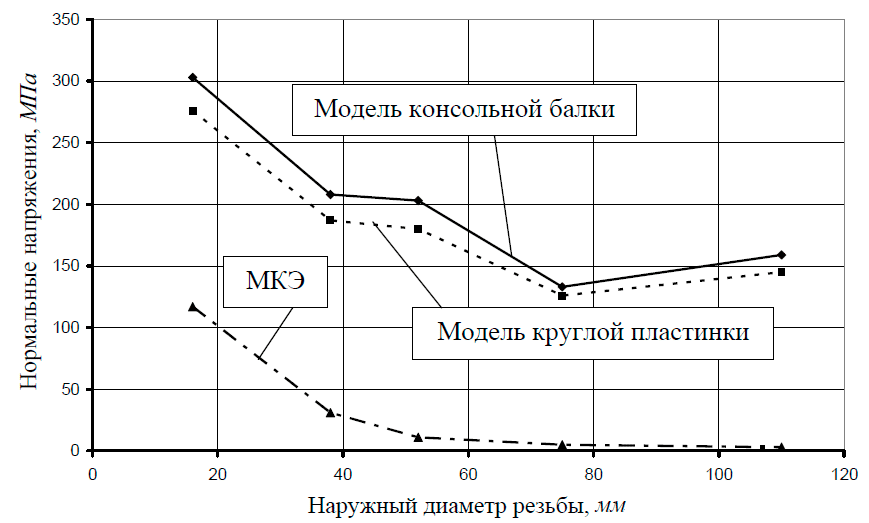
Рисунок 5 – Сравнительные результаты определения нормальных напряжений при изгибе витка резьбы
Выводы
Расчетные модели витка резьбы в виде консольной балки и в виде круглой пластинки дают практически одинаковые результаты. При этом следует отметить, что модель витка в виде круглой пластинки значительно сложнее.
Учитывая опыт прменения метода конечных элементов, можно считать, что этот метод наболее полно отражает напряженное состояние в детали. Применительно к расчету витка резьбы на изгибную прочность нормальные напряжения, найденные по методу конечных элементов очень малы, и поэтому ими можно пренебречь. Следовательно, справедливость предложения Решетова Д. Н. о нецелесообразности расчета витков резьбы на изгибную прочность можно считать доказанной.
Список использованной литературы
1. Детали машин, Павлов Я.М., изд-во «Машиностроение» 1968. – 448 с.
2. Решетов Д. Н. Детали машин. – М., «Машиностроение», 1989. – 496 с.
3. Жуковский Н. Е. Распределение давлений на нарезках винта и гайки / Н. Е. Жуковский // Полное собрание сочинений. – М.: ОНТИ, 1937. – C. 48-54.
4. Дмитриев В. А., «Судостроение», 1970. – 792 с.
5. Биргер И. А. и др. Расчеты на прочность деталей машин / – М.: Машиностроение, 1979. – 702 с.
6. Метод конечных элементов / И. М. Бузун, А. С. Гордецкий, В. Г. Пискунов, Ю. Н. Толокнов. под ред. П. М. Варвака – К. Вища Школа. 1981. – 173 с.