Компьютеризированный подход к анализу потерь давления гидравлического клапана
Оригинальное название: Computational fluid dynamics approach to
pressure loss analysis of hydraulic spool valve
Автор: Bao Min, Fu Xin, Chen Ying
Автор перевода: Надточий А. Е.
Источник: State Key Laboratory of Fluid Power Transmission & Control, 310027, Hangzhou, P. R. China.
Аннотация
Bao Min, Fu Xin, Chen Ying. Computational fluid dynamics approach to pressure loss analysis of hydraulic spool valve В данной статье исследуется текучесть внутри гидравлического клапана с помощью CFD-способа. Для сравнения анализируются вычисленные потери давления от различных потоков массы и камерных структур, отношение между потоками, геометрия клапанов. Результаты показывают, что рациональное изменение потока и геометрии клапана значительно снижают перепад давления.
Описание
При передаче больших потоков жидкости в гидравлической системе клапаны являются причиной значительных потерь давления. Обычно потеря давления в гидравлических клапанах рассчитывается теоретически или по эмпирическим формулам. Последние разработки дают возможность достичь рационального решения потери давления в комплексном канале для различных гидравлических клапанов. В этой статье текучесть внутри гидравлического клапана исследуется с помощью CFD- способа. Для сравнения анализируются вычисленные потери давления от различных потоков массы и камерных структур, отношение между потоками, геометрия клапанов. Результаты показывают, что рациональное изменение потока и геометрии клапана значительно снижают перепад давления. Модификация клапана также способствует незначительному улучшению.
1. Введение
Применение клапанов влечет за собой большие потери давления в гидравлических передачах и системах управления. При быстром изменении мощности падение давления возрастает на несколько атмосфер [6]. Повышение эффективности клапанов будет давать большие преимущества при использовании во многих областях приминения. Численное моделирование обеспечивает существенные показания в ходе предварительного эксперимента и позволяет минимизацировать время постановки и затраты на последующий экспериментальный анализ. Это возможно, если изучить и характеристики и геометрию клапана, прежде чем он будет изготовлен.
Характеристика прохождения потока в клапане играет важное значение в диссипации энергии и системной эффективности. Многие ученые и инженеры занимаются изучением состояния потока жжидкости. Wang Linxang измеряет поле скоростей в клапанах с помощью Particle Image Velocimetry (PIV) технологии [1]. Cao Bingang изучает поле потока в тарельчатом клапане численно с помощью конечно-элементоного моделирования; Kuzumi Ito рассчитывает распределение давления в тарельчатом клапане с обтекаемыми формами [3]. Matthew J. Stevenson вывел кривую, изображающую отношение между различными фрмами клапана и падением давления [5].
В данной статье используется 3D-моделирование. При сравнении результата нескольких моделей был сделан вывод, что регулирование давления на входе и выходе клапана является наиболее рауиональным способом уменьешния потерь давления в клапане. Когда поток жидкости увеличивается, перепад давления начинает быстро возрастать и достигает значительных величин. Таким образом при больших потоках жидкости должна применяться некоторая оптимизация клапанов.
2. Модель анализа
Поток в гидравлическом клапане рассматривается как полностью турбулентный. Турбулентность описывается уравнениями K-ε модели.
2.1. Геометрия CFD-моделирования
Реальная геометрия камеры клапана является очень сложной системой, состоящей из множества ступеней и гидравлических сопротивлений (отверстия, трубы и т. д.). Подробное описание данных структур не приводится в данной работе. С другой стороны, некоторые характеристики гидравлического клапана могут быть использованы для повышения эффективности применения. Упрощение геометрии клапана может уменьшить сложность создания элементной модели. Оригинальная модель клапана показана на рис. 1, такая структура обычно используется во многих клапанах. Рис. 2 показывает регулирующий клапан, имеющий идентичную структуру. Геометрия клапана для исследований в данной работе приведена на рис. 3.
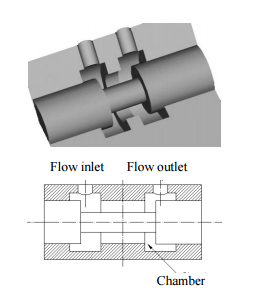
Рисунок 1 – Модель клапана
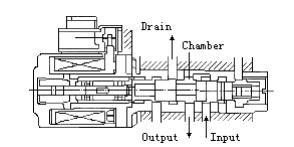
Рисунок 2 – Регулирующий клапан со структурой, подобной предыдущему
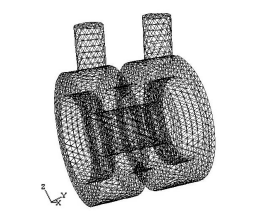
Рисунок 3 – Упрощенная геометрия зоны гидравлического клапана
2.2. Условия CFD-моделирования
Жидкость считается несжимаемой, в стационарном состоянии турбулентной в зависимости от числа Рейнольдса. Используется идельное гидравлическое масло. Плотность и вязкость зависят от температуры. Константы определены при значении идеальной температуры и низком давлении потока жидкости. Для моделирования были приняты следующие граничные условия:
- Нулевое сопротивление скорости скольжения вдоль стенок клапана.
- Постоянный поток на входе.
- Постоянное давление на выходе.
2.3. Численное решение
Основные уравнения трехмерного течения жидкости были представлены с помощью уравнения Навье-Стокса. CFD-модель является численным решением стандартной K-ε модели в области гидравлического клапана.
3.Результаты исследования
3.1. Давление при различных потоках жидкости на клапан
Для анализа влияния скорости жидкости на клапан были смоделированы несколько условий с различными потоками. Статическое давление на выходе было установлено на 5 бар.
Таблица 1 – Тестирование и результирующая матрица для геометрии клапана[кПа]
![Тестирование и результирующая матрица для геометрии клапана[кПа] Тестирование и результирующая матрица для геометрии клапана[кПа]](images/10pic4.png)

Рисунок 4 – Тенденция потери давления
В табл. 1 показана процедура испытания. Массовый расход жидкости варьируется в широком диапазоне. Рис. 4 показывает быстрое увеличение дифференциального давления потока жидкости. Эмпирическое уравнение (1) описывает перепад давления для полностью развитого турбулентного течения.
Коэффициент трения F зависит от числа Рейнольдса и шероховатости трубы. В отличие от ламинарных потоков, здесь существует нелинейная зависимость между падением давления и потоком жидкости, см рис. 4. Результаты описаны в виде эмпирического соотношения.
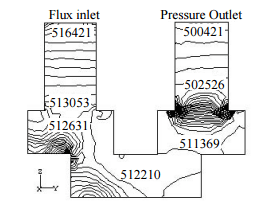
Рисунок 5 – Статическое давление контура при одном из вышеуказанных условия (Па)
На рисунке 5 статическое давление показано вдоль плоскости симметрии. Жидкость стекает с верхней стенки в отверстие через внутреннюю часть и до правого выхода. Давление увеличивается в верхней части вала перед входом из-за застоя жидкости.
На рис. 6 иллюстрируется топология потока. Разделение потока в разных уголках четко видно. Входящий поток отклоняется от стенки к краю. Одна часть площади рециркуляции находится в углу рядом с входом, с другой стороны жидкость проходит в камеру.
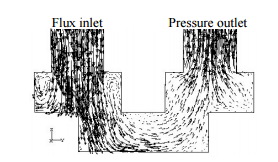
Рисунок 6 – Топология потока жидкости
Чтобы понять топологию потока важно заметить, что почти весь поток жидкости находится в верхней части камеры. Большинство нижней части остается неиспользованной. Поток переходит в верхнюю часть клапана, см рис 7. Этот переход вызывает два вихря с каждой стороны, которые соединяются в центре и проходят далее к выпускной области.

Рисунок 7 – Скоростные векторы в центральной плоскости
3.2. Влияние изменения геометрии клапана
Внезапные расширения на входе и выходе или сокрщения в поперечном сечении потока являются наиболее проблематичными в связи возникновением угловых вихрей жидкости, застоя и разделения потока, как было показано в предыдущем пункте. Это вызывает нежелательные перепады давления. Для решения этой проблемы желательно применять геометрические модификации клапана. Модифицированные клапаны должны направлять жидкость без резких изменений и возникновения так называемых мертвых зон. На рис. 8 изображены три различных вида геометрии гидравлического клапана и их подробное строение. № 1 является основным видом гидравлического клапана. В двух других модифицирована одна часть структуры.
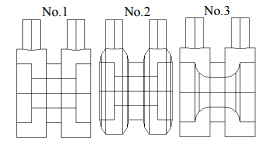
Рисунок 8 – Структуры внутренней части трех различных клапанов
Таблица 2 – Тестирование и результирующая матрица [кПа]
![Тестирование и результирующая матрица [кПа] Тестирование и результирующая матрица [кПа]](images/10pic11.png)
Таблица 2 показывает тестовую и результирующею матрицу для исходного и модифицированных клапанов.
3.3. Эффект от модификации клапана
Результаты на следующем рисунке покадывают давление жидкости на контуры и векторы изменения скорости для третьего вида клапана.
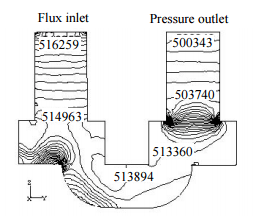
Рисунок 9 – Статическое давление на стенки модифицированного клапана (Па)

Рисунок 10 – Вектор скорости жидкости для модифицированного клапана
Как показано на рис. 9, статическое давление было увеличено близко к критической точке – тот же эффект, что и на рис. 5. В области выхода плотность линий показывает высокий градиент давления. На рис. 10 показаны векторы скорости. Видно, что резкое изменение формы на валу клапана вызвало рециркуляции в углу. Кроме того, в остальные углы поток не подается. Таким образом, такая модификация мало способствует улучшению. В 2D состоянии модификация клапана может не спровоцировать поворота течения во входной области, но в 3D-модели может возникнуть движение вокруг оси, поэтому такая модификация не может быть применима из-за потери давления, аналогичной с оригинальным клапаном. Рис. 11 отображает вектор скорости потока жидкости в лицевой части клапана.

Рисунок 11 – Вектор скорости жидкости в 3D-модели
3.4. Эффект от модификации клапана на входе и выходе
Клапан может быть так же модифицирован на входе и выходе.
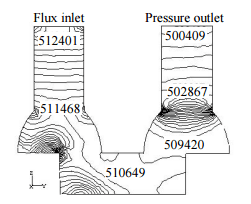
Рисунок 12 – Давление на стенки модифицированного клапана (Па)

Рисунок 13 – Вектор скорости жидкости в осевой плоскости
На рис. 13 показаны векторы скорости. По сравнению с рис. 10, весь поток имеет меньшую турбулентность. Практически не наблюдается разделение на области. Жидкость течет более привязанно к стенкам. Кроме того, на входе меньше вихрей, чем раньше. Падение давления меньше, чем в двух других моделях.
4.Выводы
Была проанализирована зависимость между геометрией клапана и потерей давления потока жидкости. Результаты показывают, что более важна форма клапана на входе и выходе. Видоизмененный клапан уменьшает турбулентность и, как следствие этого, шумы и потерю давления. При проектировании клапанов следует применять некоторую оптимизацию геометрии.
Результаты моделирования показали, что модификация на входе и выходе является наиболее успешным способом улучшения клапана в отношении снижения потери давления.
С использованием CFD-моделирования возможно изучить характеристики клапана, провести оптимизацию их геометрии до того, как он будет изготовлен. Результаты такого моделирования могут быть полезны для различных гидравлических конструкций, в состав которых входят различные виды клапанов.
Список источников
- Wang Linxiang, Chen Ying, Ruan Xiaodong, Lu Yongxiang. Experiment Study on Fluid Flow in Fluid Power System. – ICFP 97, 1997.
- Cao Bingang. Numerical study on fluid flow in poppet valve by boundary element method // Machine Tool and Hydraulics. – 1991.
- Kazumi ITO. Flow in a poppet Valve / Proc of 1th international symposium on FPTC, – Beijing, China, 1991.
- James A. Sullivan. Fluid Power Theory and Application Third Edition. – Prentice Hall inc., 1989.
- ] Matthew J. Stevenson & Xiao Dong Chen. Visualization of Flow Patterns in a High-pressure Homogenizing Valve Using a CFD Package // Journal of Food Engineering, 33. – 1997.
- G. Bella , M. Burroni, M.M. Cerimele, F. Pistella. A simulation tool for the analysis of high speed flows // Mathematics and Computers in Simulation, 51. – 1999.
- Francesco Maisano, Alberto Redaelli, Giancarlo Pennati et al. The hemodynamic effects of doubleorifice valve repair for mitralregurgitation: a 3D computational model // European Journal of Cardiothoracic Surgery, 15. – 1999.