Разработка технологии изготовления внутренних пространственных зацеплений

Для обеспечения связи между агрегатами в машиностроении широко используют зубчатые муфты. Однако геометрия зацепления зубчатой муфты позволяет компенсировать небольшие перекосы осей соединяемых валов до ω=1,5°. Это связано с тем, что угловые расположения осей наружного зубчатого венца относительно внутреннего венца вызывают смещение зубьев, которые ведут к появлению неравномерных зазоров между зубьями, при этом количество зубьев, находящихся в зацеплении уменьшается, а нагрузка на зубья увеличивается. Кроме того, наличие угловых и тангенциальных смещений зубьев относительно друг друга в зацеплении ведет к возникновению кромочных контактов зубьев. При этом в настоящее время практика требует увеличения компенсирующей способности зубчатых муфт и повышения их долговечности.

Решить эти проблемы можно за счет создания новой геометрии внутренних пространственных зацеплений.

На рис.1 представлено внутреннее пространственное зацепление с зубьями эвольвентного профиля, которые взаимодействуют в условиях перекоса осей наружного (втулка) и внутреннего (обойма) зубчатых венцов. Здесь показано: 1 - ось наружного зубчатого венца, 2 - ось внутреннего зубчатого венца, 3 - зуб наружного зубчатого венца (втулки), 4 - зуб внутреннего зубчатого венца (обоймы), 5 - внутренний зубчатый венец (обойма). В точках b и с особые положения зубьев втулки относительно обоймы [1].

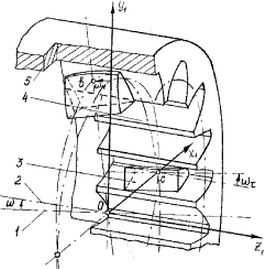
Рисунок 1 – Особые положения зубьев пространственного зацепления с равным числом внутренних и наружных зубьев при наличии перекоса осей элементов

Уравнение связи между координатами x₁,y₁,z₁ (обоймы) и x₂,y₂,z₂ (втулки) в относительных движениях определяется уравнениями [1]:

где ψ - угол поворота внутреннего пространственного зацепления; ω - угол перекоса осей валов втулки и обоймы.

Переход от системы координат x₁,y₁,z₁ к системе координат x₂,y₂,z₂, имеющих единое начало координат, можно осуществить при помощи последовательного выполнения трех поворотов a, b, c (рис. 2) вокруг себя осей координат путем задания трех углов Эйлера в трехмерном эвклидовом векторном пространстве.

Рисунок 2 –Структура движений при преобразовании систем координат в относительных движениях огибающей и огибаемой поверхности зубьев внутренних пространственных зацеплений при наличии перекоса осей

Учитывая уравнения эвольвентного профиля инструмента [3], основные положения кинематического метода исследования пространственных зацеплений, приведенного в работе [2], основываясь на втором способе Оливье, уравнения контактных линий в системе инструмента с эвольвентным профилем зубьев имеют следующий вид:

где r_b – радиус основного цилиндра инструмента;
φ – параметрический угол эвольвенты.

Здесь:

где z – число зубьев инструмента;
invα_ω – эвольвентный угол, соответствующий точке профиля на делительном цилиндре.

Уравнения данной системы позволяют найти положения линий контакта зубьев на профиле зуба инструмента (обоймы) в зависимости от угла поворота зацепления ψ при вращении.

Список использованной литературы

1. Михайлов А.Н. Разработка методов повышения несущей и компенсирующей способности зубчатых муфт: Дис. …канд. техн. наук.- Донецк: ДПИ, 1985.- 259 с.
2. Литвин Ф.Л. Теория зубчатых зацеплений.- М.: Наука, 1968.- 584 с.
3. Михайлов А.Н., Рыбина С.А., Перов Д.В., Оливер Т., Бемент М. Основы синтеза геометрии внутренних пространственных зацеплений с равным числом внутренних и наружных зубьев./ Прогрессивные технологии и системы машиностроения. Сб. научн. трудов. – Донецк: ДонГТУ, 2000. Вып. 10. С. 149-161.