Українська   Русский
DonNTU   Masters' portal

Contents

Introduction

Large masses of the machine, moving at high speed, causing the complex dynamic processes during starting and braking. Dynamic processes form the excessive load, progressive fatigue phenomena of individual structural elements that lead to emergencies and disasters.

To increase reliability, safety and durability of machines designing and manufacturing them should take into account the impact of dynamic forces. The theoretical foundation of dynamic calculations is the theory of mechanical oscillations. Knowledge of the laws of oscillatory processes allow the rational machinery design..

1. Relevance of the topic

Construction of mathematical models of operation of the elevator installation will allow in the future a more detailed study of the work of some of its units to select their optimum performance. This in turn will increase the safety of the elevator installation, which is especially important when considering the passenger facilities, optimize the speed characteristics, as well as depreciation of equipment to explore the dynamic effort to further eliminate existing problems.

2. The purpose and objectives of the study

The aim of this work is the mathematical modeling of dynamic processes hoists with a large rope length.

The main tasks of modeling:

  1. Derivation of the equations of motion for the two types of machines.
  2. The definition of a rational number of elastic rope masses.
  3. Simulation of operating mode lifting machine.

3. Review of Research and Development

Research and reduce the dynamic loads in the ropes for mine lifts engaged in the twentieth century scholars such as A. I. Dinnik [1–4], S. P. Timoshenko [5–7], M. M. Fedorov [8], F. V. Florinskiy [9], G. N. Savin [10, 11], A. N. Golubentsev [12], L. V. Kolosov [13, 14] and others.

The current state of the question of dynamic loads in lifting machine described in the works of such prominent scientists as V. I.  Dvornikov [15–17], A. G. Stepanov [18–21] and others.

4. Mathematical modeling of dynamic processes lifting machine with one end of the rope with a large rope length

Lifting the load in the vertical trunk will occur according to the scheme shown in Fig. 1.

Schematic model lifting machine with one end of the rope

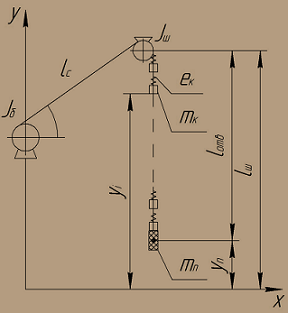
Figure 1 – Schematic model lifting machine with one end of the rope

Lifting machine consists of a drum machine given to him moments of inertia of the rotating parts of the gear motor and the rotor with the kinetic moment of inertia Jб, guide pulley with the moment of inertia Jш, inclined string rope lcтр, counting unchanging in time and steep part of the rope lотв, which secured the cargo weight limit mn.

Sheer rope winding machine is divided into a number of distributed mass mk coordinates yi, interconnected elastic connections ek. Limit load mn is moving yn vertical measured from a starting position of the load.

After making the necessary calculations derived from the Lagrangian, which represents the difference between the kinetic and potential energy of the system, as well as taking into account that for each segment of the rope are elastic-dissipative forces, arranged in parallel, as a result we obtain the desired equation of motion:

Equation of motion.

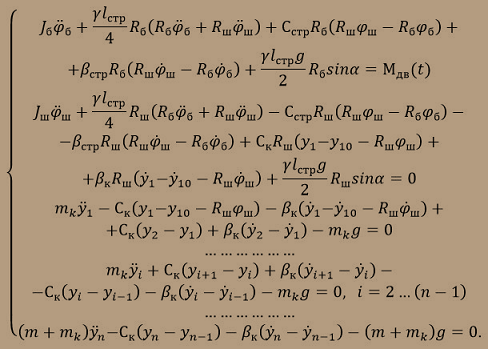Conclusion

The resulting equations of motion and allow to trace the resilient and gravitational effects acting on the drum, the pulley, the load and the rope on each segment during the starting of the machine, its operation and deceleration. This method of determining the dynamic forces in the rope can be used for other lifting machines.

In writing this essay master's work is not yet complete. Final completion: December 2015. Full text and materials on the topic can be obtained from the author or his manager after that date.

List of sources

  1. Динник А. Н. Динамические напряжения в подъемном канате при внезапной остановке верхнего конца / А. Н. Динник. – Южный инженер, 1917. – № 3-4.
  2. Динник А. Н. Кручение. Теория и приложение / А. Н. Динник. – М., 1938.
  3. Динник, А. Н. Устойчивость упругих систем : учеб. пособие для ун-тов / акад. А. Н. Динник, проф. Днепропетр. металлург. ин-та. – М. : ОНТИ НКТП СССР, Гл. ред. общетехн. лит. и номографии, 1935. – 183 с.
  4. Кожухов А. А., Очинский В. В. Академик А. Н. Динник (к 130-летию со дня рождения) // Исследования по истории физики и механики 2006. – М.: Наука, 2007. – С. 239-248.
  5. Тимошенко С. П. Колебания в инженерном деле / С. П. Тимошенко, Д. Х. Янг, У. Уивер ; пер. с англ. Л. Г. Корнейчука. – М. : Машиностроение, 1985. – 472 с.
  6. Тимошенко С. П. О вынужденных колебаниях призматических стержней / С. П. Тимошенко. – Киев: тип. С. В. Кульженко, 1909. – 50 с.
  7. Тимошенко С. П. Статистические и динамические проблемы теории упругости / С. П. Тимошенко. – Киев: Наукова думка, 1975. – 564 с.
  8. Федоров М. М. Методология динамической теории расчета подъемного каната вертикальных шахт / М. М. Федоров // Записки института горной механики. АН УССР. – 1936. – № 1.
  9. Флоринский Ф. В. Динамика шахтного подъемного каната / Федор Валентинович Флоринский. – М. : Углетехиздат, 1955. – 238 с.
  10. Савин Г. Н. Динамическая теория расчета шахтных подъемных канатов / Г. Н. Савин. – К. : Из-во АН УССР, 1949. – 238 с.
  11. Савин Г. Н. Динамика нити переменной длины / Г. Н. Савин, О. А. Горошко. – К. : Из-во АН УССР, 1949. – 332 с.
  12. А. Н. Голубенцев, Динамика переходных процессов в машинах со многими массами / А. Н. Голубенцев. – Москва: ГНТИ, 1959.
  13. Колосов Л. В., Потураев В. Н., Червоненко А. Г., Безпалько В. В., Завозин Л. Ф. Вертикальный транспорт на горных предприятиях / Л. В. Колосов, В. Н. Потураев , А. Г. Червоненко, В. В. Безпалько, Л. Ф. Завозин. – М.: Недра, 1975. – 350с.
  14. Гаркуша Н. Г., Колосов Л. В., Обухов А. Н. и др. Подвесные устройства шахтных подъемных сосудов. Под ред. Н. Г. Гаркуши / Н. Г. Гаркуша, Л. В. Колосов, А. Н. Обухов. – М.: Недра, 1980. – 105 с.
  15. Дворников В. И. Теоретические основы динамики шахтного подъемного комплекса / В. И. Дворников, Е. Р. Къерцелин. – София, МОНТ, 1997. – 363 с.
  16. Дворников В. И., Къерцелин Е. Р., Трибухин В. А., Савенко Э. С. Динамические жесткости канатов шахтных подъемных установок / В. И. Дворников, Е. Р. Къерцелин, В. А. Трибухин, Э. С. Савенко // Стальные канаты. – Одесса, 2003. – Вып. 3.
  17. Шахтный подъем: Научно-производственное издание / В. Р. Бежок, В. И. Дворников, И. Г. Манец, В. А. Пристром; общ. ред. Б. А. Грядущий, В. А. Корсун. – Донецк : ООО «Юго-Восток Лтд», 2007. – 624 с.
  18. Степанов А. Г. Динамика шахтных подъёмных установок / Анатолий Григорьевич Степанов. – Пермь : УрО РАН, 1994. – 263 с.
  19. Степанов А. Г. Динамика машин / А. Г. Степанов. – Екатеринбург: Российская академия наук, 1999. – 392 с.
  20. Степанов А. Г., Корняков М. В. Динамика машин : монография. 2-е изд., испр. и доп. / А. Г. Степанов, М. В. Корняков. – Иркутск : Изд-во ИрГТУ, 2014. – 412 с.
  21. Степанов А. Г. Динамические процессы при скольжении канатов по футеровке барабана многоканатной подъемной установки / А. Г. Степанов // Горное оборудование и электромеханика. № 6, 2010. – C. 24-35.