Компьютерное моделирование и моделирование динамики гибкого подъемного каната с изменяющейся во времени длиной

Аннотация

Jihu BAO, Peng ZHANG, Changming ZHU. Computing Simulation and Dynamics Modeling of Flexible Hoisting Rope with Time-varying Length Изучены нелинейные колебания гибкого подъемного каната с изменяющейся во времени длиной. Гибкий подъемный канат смоделирован как упругая нить с концевым грузом.

Описание

Изучена нелинейная вибрация гибкого подъемного каната с изменяющейся во времени длиной. Гибкий подъемный канат моделируется как упругая нить с концевым грузом. Представлена систематическая процедура для выведения модели колебаний гибкого подъемного каната. Уравнения разработаны с использованием принципа Гамильтона, учитывая сцепление осевого перемещения и изгибную деформацию каната. Получены нелинейные дифференциальные уравнения с изменяющимися во времени коэффициентами. Для численного анализа результата уравнения используется MATLAB. Кроме того, для оценки теоретической модели выполняются эксперименты и моделирование и обнаружено, что экспериментальная данные согласуются с теоретическим материалом. Таким образом, подтверждается математическая модель гибкого каната подъемной системы. Результаты моделирования и эксперимента показывают, что гибкая система рассеивает энергию во время движения вниз (таким образом, стабилизированного), но получает энергию во время восходящего движения (таким образом, нестабилизированный).

Ключевые слова: поперечные колебания; гибкий подъемного каната; теоретическая модель; MATLAB

1. Введение

В то время как канат используется в отраслях грузоподъемной промышленности, таких как шахтные подъемники, лифты, краны и т.д., он подвергается колебаниям из-за его высокой гибкости и относительно низких внутренних демпфирующих характеристик [1, 2].Изучение проблем колебания канатов в подъемных системах привлекает широкое внимание. Chi [3] вычисляет собственные частоты, связанные с вертикальным колебанием стационарного каната в сочетании с кабиной лифта. Terumichi [4] предполагал, что скорость каната является постоянной и изучал поперечные колебания каната с изменяющейся во времени длиной и массо-пружинной системой на конце каната теоретическими и экспериментальными методами. Fung [5] проанализировал поперечные колебания каната лифта с изменяющейся во времени длиной и временем изменения массы и инерции ротора. С помощью системы управления он предложил подавить переходные амплитуды колебаний. Kaczmarczyka [6] изучал колебания подъемного каната в сочетании с большой глубиной шахты и построил модель с распределенными параметрами. Он обнаружил, что вибрации в контактной вертикальной тросовой системе может включать ряд резонансных явлений. Zhang [7] вывел уравнение, регулирующее сочетание колебаний гибкой системы кабельного транспортера со сколь угодно разной длиной. Zhu [8] исследовал контроль лифта с канатом теоретическими и экспериментальными методами. Он разработал экспериментальный метод для проверки неконтролируемого и контролируемого поперечных колебаний движущегося каната в высотном лифте и показал, что полученные данные согласуются с теоретическими материалами. Zhang [9] представил систематическую процедуру для получения модели системы кабельного транспортера с произвольно меняющейся длиной каната и предложил контроллер Ляпунова для рассеивания вибрационный энергии. Zhang и др. [10] вывели определяющее уравнение и уравнение энергии продольных колебаний подъемного каната с различной длиной.

В то время, как обширные исследования сосредоточены на вибрационных характеристиках каната с изменяющейся во времени длиной, динамическая устойчивость каната также была изучена несколькими исследователями. Kumaniecka [11] исследовали продольно-поперечные колебания подъемного каната с медленой изменяющимися параметрами. Учитывая материал каната и его нелинейность, нестабильные участки были определены с применением метода гармонического баланса. Стабильность продольных и поперечных колебаний каната с произвольным изменением длины и различные граничные условия при этом были изучены Zhu и др. [12]. В то время, как амплитуда смещения может вести себя по-разному в зависимости от граничных условий, амплитуда вибрационной энергии переводится из среднего опускания и поднятия в расширение и втягивание соответственно.

Обширные научно-исследовательские работы над гибким подъемным канатом с изменяющейся во времени длиной были проведены в последние несколько десятилетий, как упомянуто выше, однако, большинство исследований были ограничены случаями с постоянной скоростью каната. Динамические характеристики гибкого подъемного каната произвольно изменяющейся длины являются предметом данного исследования. Основные уравнения разработаны используя расширенный принцип Гамильтона. Полученные уравнения приведены в нелинейные дифференциальные уравнения с переменными коэффициентами. При выборе надлежащего функционального режима, удовлетворяющего граничным условиям, решение основных уравнений было получено с помощью метода Галеркина. Для того чтобы оценить математическую модель, провелась экспериментальная настройка и некоторые эксперименты. При сравнении экспериментальных данных с моделированием получен благоприятный результат, что указывает на то, что предлагаемая математическая модель справедлива для гибкого подъемного каната. На основе предложенного фундаментального динамического анализа подобный метод контроля колебаний может быть принят для подобных подъемных систем с гибким тяговым оргном.

2. Модель гибкой подъемной системы

Гибкая подъемная система может быть упрощена аксиально скользящим канатом с изменяющейся во времени длиной и концевым грузом, как показано на рис. 1. Канат имеет модуль Юнга E, диаметр D и плотность за единицу длины ρ. Начальные координаты установлены в верхнем конце ствола – мгновенная длина каната l(t) в момент времени t. Мгновенная скорость и ускорение каната являются v(t)=l'(t) и a(t) = v'(t) соответственно, где ' обозначает дифференцирование по времени. В любой момент t поперечное смещение каната описывается у(х; t) в пространственном положении х, где 0?х?l(t).

Следующие допущения ограничивают анализ:

1. Модуль Юнга, диаметр и плотность каната всегда постоянны.
2. Учитывается только поперечное колебание каната. Эластичное удлинение каната, возбужденного от поперечных колебаний значительно меньше, чем длина каната.
3. Жесткость на изгиб струны, трение и влияние воздушного потока игнорируются.

Кинетическая энергия гибкой подъемной системы вычисляется

Упругая энергия деформации струны

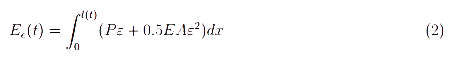
где: Р(х,t)=[m+(l(t)-x)](g-a) – напряжение в пространственной координате х каната в момент времени t, ξ представляет собой меру деформации при пространственном положении х каната. Согласно характеристики верхнего ограничения каната, граничные условия на х(t) = 0 и

При замещении уравнений (1) и (2) по принципу Гамильтона

применяется операция вариационного и упорядоченного интегрирования по частям, чтобы получить

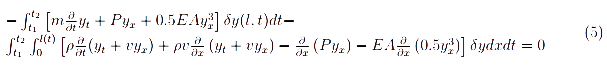
Приравнивание коэффициентов δy в уравнении (5) к нулю дает основное уравнение в виде

Первые четыре члена в уравнении (6) соответствуют касательным и центростремительным ускорениям Кориолиса, соответственно энергия, связанная с поперечной вибрацией системы:

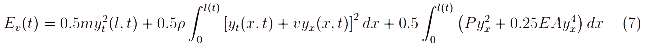
3. Дискретизация основных уравнений

В этом разделе применяется метод Галеркина для усечения бесконечного частного дифференциала в нелинейном конечном обыкновенном дифференциальном уравнении с варьирующимися во времени коэффициентами. Решение производится численными методами. Для отображения уравнения (6) на фиксированной области вводится новая независимая переменная ζ=х/[l(t)] во временной области [0; l(t)] для х и преобразуется в фиксированной области [0; 1] для ζ. По характеристике упругого каната, решение поперечной вибрации у(х; t) предполагается в виде [7, 12]

где: q_i(t)(i=1, 2, 3,..., n) является обобщенной координатой для у(х; t), n - число включенных режимов. φ_i(ζ) является пробной функцией [7, 12]

Следовательно, расширение уравнения (8) приводит к выражениям в частных производных поперечной функции колебания:

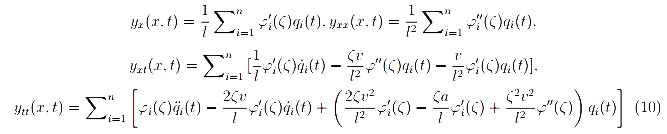
Подставление(10) в (6), умножение уравнения на φ_j(ζ)(i=1, 2, 3,..., n), интегрирование его по ζ= 0...1, и использование граничных условий и ортонормальности отношения для φ_i(ζ) дают дискретизованное уравнение поперечных колебаний для гибкого подъемного каната с вариативным коэффициентом времени

где: Q – это вектор обобщенных координат; М, С, К и F – матрицы массы, колебаний, жесткости и обобщенной силы по отношению к Q соответственно. S(Q) – порядок обобщенных координат.

4. Моделирование и эксперименты

Чтобы проверить математическую модель, экспериментальная установка гибкой подъемной системы построена как на рис. 2 (а). Установка, имитируя подъемный лифт с упругим тяговым органом, состоит их тяговой системы, системы направляющих и системы сбора данных. Привеняется мотор преобразования частоты. Скорость вращения двигателя может регулироваться путем регулирования выход преобразователя для получения кривой движения системы подъема. Тонкий стальной канат с диаметром 3,2 мм выбран в качестве подъемного каната. Модель противовеса состоят из многих весов. Масса противовеса изменчива, возможно увеличение или уменьшение количества веса. Подъемный каната является основным объектом исследования, его поведение будет изучатся на данной модели установки. Микро-датчик с массой 4 г присоединен в определенном положении каната, чтобы измерять поперечного ускорение колебания каната. Сигналы от микро-датчика передаются на компьютер и сохраняются. Рис. 2 (б) дает фактическое описание экспериментальной установки.

4.2. Экспериментальная процедура

Теперь поперечные колебания гибкой подъемной системы будут рассчитываться по теоретическими уравнение и одновременно с проведением эксперимента на экспериментальной установке. Результаты будут сравниваться. Все параметры, использованные в расчете и испытании, полностью совпадают. Смещение вниз или вверх противовеса описано в ходе теоретических исследований.В начале противовес находятся наверху и по мере работы установки, опускается вниз. При достижения низа, противовес останавливается на мгновение и возвращается обратно. Параметры гибкой системы: ρ = 0.042 кг/м, m = 15 кг, ЕА = 6.3 * 10⁶ Н. Максимальная высота подъема, скорость и ускорение - 3,8 м, 0.55м/с и 0,4 м/с² соответственно. Время прохождения расстояния 3,8 м составляет 8 сек. Рисунок. 3 дает описание перемещения, скорости и ускорения, кривые гибкой системы подъема, процессы ускорения, торможения и равномерной скорости при движении вверх и вниз. Используя кривые как исходные данные для уравнения (11) с помощью MATLAB можно соделировать поперечные колебания гибкого каната. Моделирование с использованием MATLAB является хорошим способом для изучения алгоритмов [13]. С помощью MATLAB разработаны имитационные модели для достижения различных основных параметров оценки, что имеет большое значение при решении нелинейных дифференциальных уравнений с изменяющимися во времени коэффициентами. В данной работе все численные анализы были выполнены с помощью MATLAB.

4.3. Экспериментальные результаты

Численные эксперименты с точными параметрами эксперимента проводятся для того, чтобы сравнить с моделированием. Таким образом, можно сделать вывод, что теоретические уравнения, предложенные в данной работе, могут быть использованы для оценки вибрации гибкого подъемного каната.

Рисунок 4(А) показывает ниспадающие амплитуды колебаний с увеличением длины каната во время движение вниз. Это связано с тем, что подъемный канат диссипативен во время нисходящего движения, что приводит к стабилизации его поперечной динамической реакции, как показано на рис. 5(а). Частоты поперечных колебаний падают с увеличением длины каната. Это связано с тем, что масса каната увеличивается, а жесткость снижается, то есть, канат становится несколько мягче.

Напротив, на рис. 4(B), заметно, что амплитуды колебаний возрастают с уменьшением длины каната во время восходящего движения. Увеличение энергии в канате во время движения вверх, таким образом, приводит к нестабилизировнным поперечным динамическим реакциям, как показано на рис. 5 (б). В то же время частоты поперечных колебаний увеличиваются при уменьшении длины каната. Это связано с тем, что масса каната уменьшается, а жесткости увеличивается, то есть, канат становится несколько жестче.

5. Заключение

Гибкая система моделируется как аксиально скользящий канат с изменяющейся во времени длиной и концевым грузом. Основные уравнения выводятся с помощью правила Лейбница и принципа Гамильтона. Метод Галеркина используется для усечения бесконечномерных частичных дифференциальных уравнений в совокупности с нелинейными конечномерными обыкновенными дифференциальными уравнениями с вариативными временными коффициентами. Для проверки теоретической модели построена экпериментальная установка и проведены некоторые эксперименты. Сравниваемые результаты математического и экспериментального моделирования согласованы между собой, что подтверждает математическую модель гибкой подъемной системы. На основании моделирования и эксперимента можно сделать следующие выводы: Гибкий подъемный канат с изменяющейся во времени длиной испытывает нестабильность во время восходящего движения, собственные частоты увеличиваются с увеличением жесткости каната и энергии, преобразуемой от аксиального перемещения в гибкую деформацию. Напротив, система стабильна во время нисходящего движения, собственные частоты снижаются из-за увеличения массы и уменьшения жесткости каната, происходит преобразовывание гибкой деформации в осевое перемещение. Предложенная теоретическая модель и анализ динамической характеристики гибкой подъемной системы в этой статье будет полезны исследователям для понимания ее динамического поведения и определения методов подавления колебаний.

Список источников

1. S. Kaczmarczyk, The passage through resonance in a catenary-vertical cable hoisting system with slowly varying length, Journal of Sound and Vibration, 1997, 282 (2), pp. 243-269.
2. S. Kaczmarczyk and W. Ostachowicz, Transient vibration phenomena in deep mine hoisting cables part1: Mathematical model, Journal of Sound and Vibration, 2003, 262, pp. 219-244.
3. R. M. Chi and H. T. Shu, Longitudinal vibration of a hoist rope coupled with the vertical vibration of an elevator car, Journal of Vibration and Acoustics, 1991, 148 (1), pp. 154-159.
4. Y. Terumichi, M. Ohtsuka, M. Yoshizawa, Y. Fukawa and Y. Tsujioka, Nonstationary vibrations of a string with time-varying length and a mass-spring system attached at the lower end, Nonlinear Dynamics, 1997, 12, pp. 39-55.
5. R. F. Fung and J. H. Lin, Vibration analysis and suppression control of an elevator string actuated by a pm synchronous servo motor, Journal of Sound and Vibration, 1997, 206 (3), pp. 399-423.
6. S. Kaczmarczyk and W. Ostachowicz, Transient vibration phenomena in deep mine hoisting cables part2: Numerical simulation of the dynamic response, Journal of Sound and Vibration, 2003, 262, pp. 245-289.
7. Y. H. Zhang and Sunil Agrawal, Coupled vibrations of a varying length flexible cable transporter system with arbitrary axial velocity, Proceeding of the 2004 American control conference, 2004, pp. 5455-5460.
8. W. D. Zhu and Y. Che, Theoretical and experimental investigation of elevator cable dynamics and control, Journal of Vibration and Acoustics, 2006, 128, pp. 66 – 78.
9. Y. H. Zhang, Longitudinal vibration modeling and control a flexible transporter system with arbitrarily varying cable lengths, Journal of Vibration and Control, 2005, 11, pp. 431-456.
10. P. Zhang, C. M Zhu and L. J Zhang, Analyses of longitudinal vibration and energetics on flexible hoisting systems with arbitrarily varying length, Journal of Shanghai JiaoTong University, 2008, 42 (3), pp. 480-483, 488.
11. A. Kumaniecka and J. Niziol, Dynamic stability of a rope with slow variability of the parameters, Journal of Sound and Vibration, 1994, 178, pp. 211-226.
12. W. D. Zhu and J. Ni, Energetics and stability of translating media with an arbitrarily varying length, Journal of Vibration and Acoustics, 2000, 122 (7), pp. 295-304.
13. X. G. Wu and T. W. Guo, Direction of arrival parametric estimation and simulation based on MATLAB, Journal of Computational Information Systems, 2010, 6 (11), pp. 4723-4731.