К вопросу о динамике и оптимизации шахтных подъемников
Автор: Осипова Т. Н., Нестеров А. П.
Источник: Машинобудування: Збірник наукових праць 2014 р. №13
Аннотация
Осипова Т. Н., Нестеров А. П. К вопросу о динамике и оптимизации шахтных подъемников В статье рассматриваются вопросы, выполненные учеными в области динамики и оптимизации шахтных подъемников. Для определения динамических нагрузок в подъемниках их рассматривают как многомассовую механическую систему с упругими связями. Упругие связи представляют как стержень с распределенной массой или невесомым.
В статье рассматриваются вопросы, выполненные учеными в области динамики и оптимизации шахтных подъемников. Для определения динамических нагрузок в подъемниках их рассматривают как многомассовую механическую систему с упругими связями. Упругие связи представляют как стержень с распределенной массой или невесомым.
Ключевые слова: шахтный подъемник, динамика, оптимизация, многомассовая система, минимизация, осциллограмма.
1. Актуальность
В процессе эксплуатации шахтных подъемных установок возникают вертикальные колебания клетей на канатах в результате пуска и остановки электродвигателя, рабочего и экстренного торможений барабана механическими тормозами, посадки и снятии клетей с жесткого основания.
Колебательные процессы в канатах подъемников вызывают увеличение динамических нагрузок и напряжения в элементах подъемников.
2. Основной материал
Вопросами исследования и уменьшения динамических нагрузок в валопроводе и канатах шахтных подъемников занимались такие ученые, как А. И. Динник, С. П. Тимошенко, М. М. Федоров, Ф. В. Флоринский, Г. Н. Савин, О. А. Горошко, С. Н. Кожевников, А. Н. Голубенцев, Н. Г. Гаркуша, В. Н. Потураев, Л. В. Колосов, В. В. Безпалько, А. П. Нестеров, В. И. Дворников, В. М. Чермалых, А. Г. Степанов, В. С. Ловейкин, Р. Л. Мищенко, Э. С. Савенко, Л. М. Козарь и др.
Отметим, что для изучения и определения динамических нагрузок в подъемниках их рассматривали как многомассовую механическую систему с упругими связями. Упругие связи – канаты – представляли как стержень с распределенной массой [1–8] или невесомым [6, 7, 9–14].
Оценку потенциальной и кинетической энергий упругой системы с распределенной массой и невесомой системы впервые выполнил Рэлей [10]. Он выдвинул гипотезу, что характер деформаций весомой упругой связи при динамических нагрузках с достаточной точностью можно выразить деформацией при статическом нагружении. Для вертикальных канатов деформацию можно представить изменяющейся по линейному закону. С. П. Тимошенко [9] показал, что для невесомого каната, один конец которого защемлен (неподвижен), а на другом висит груз, частота колебаний груза будет практически одинакова системе «весомый канат – груз», если рассматривать канат как невесомый стержень и к грузу прибавить одну треть массы каната. Этот результат адекватен прибавлению одной трети массы каната от узла колебаний, то есть от точки, амплитуда колебаний которой равна нулю. С. Н. Кожевников [11] распространил его на валопровод металлургических машин, А. Н. Голубенцев [13] использовал его для шахтных подъемников, А. П. Нестеров [41] применил для многоканатных подъемных установок с хвостовыми канатами. А. Г. Степанов [7] исследовал динамику шахтных подъемных установок при аварийном торможении, использовав метод Рэлея.
А. П. Нестеров указывает на то, что дополнительные динамические нагрузки в элементах подъемников можно определить, рассматривая подъемники как многомассовые системы, состоящие из дискретных масс, соединенных между собой упругими связями [14]. Также в его работе приведены различные динамические эквивалентные крутильные схемы подъемников и показан вывод дифференциальных уравнений силовых переходных процессов в моментах сил упругости для многомассовых крутильных систем, используя уравнение Лагранжа ІІ рода и методику С. Н. Кожевникова [11].
Г. Н. Савин [4] развил теорию расчета динамики каната, введя понятие «динамического коэффициента запаса прочности, учитывая явление усталости». Им приведены значения коэффициентов запасов прочности канатов в верхнем и нижнем сечениях. Ф. В. Флоринский [3] обобщил теоретические исследования многих ученых и предложил новые методы расчета весомого подъемного каната в виде простых формул и таблиц. Им рассмотрены задачи динамики каната как весомого упруго–вязкого стержня с грузом на конце при условии, когда верхней конец каната имеет ускорение. Различные задачи динамики подъемной установки с весомыми канатами постоянной длины решал А. Г. Степанов [7], а переменной длины – Г. Н. Савин и О. А. Горошко [5]. В. И. Дворников [6, 15], Р. Л. Мищенко [8] и другие рассматривали различные виды деформаций в канатах на основании уравнений в частных производных.
На основании выше изложенного сделаем вывод о том, что динамику подъемников можно с достаточной инженерной точностью определять при невесомых канатах и валах.
Минимизацией динамики машин занимались многие ученые: в машиностроении [16–21], вибрационной технике [22–24], в транспорте [25, 26], в лифтах [27–29] и др.
Минимизацией грузовых и режимных параметров подъемных машин впервые начал заниматься М. М. Федоров [30, 31]; переходных процессов – А. Н. Голубенцев [12, 13]; силовых стационарных процессов – А. П. Нестеров [32–35]; эффективной мощности электродвигателей – Б. Л. Давыдов [36], Б. Я. Левин и С. Б. Браиловский [37], В. М. Чермалых [38], А. С. Масляный [39], В. В. Гамаюнов [40], В. С. Ловейкин [27, 41]; выбора оптимальной грузоподъемности скипа – М. М. Федоров [30], Г. М. Еланчик [42], З. М. Федорова [43].
А. П. Нестеров [14] указывает, что «подбирая динамические параметры, можно оптимизировать силовые переходные процессы, возникающие при работе подъемников, то есть максимально уменьшить динамические нагрузки, вызванные колебательными процессами. Динамическими параметрами подъемников можно варьировать, изменяя конструкцию вращающихся масс, вводя упругие вставки и дополнительные демпфирующие устройства. Чтобы уменьшить динамические нагрузки в упругих связях подъемников необходимо изменять одновременно все динамические параметры, то есть проводить многопараметрическую оптимизацию. А. П. Нестеровым введено понятие функции цели для подъемников, в качестве которой для оптимизации переходного процесса в механических системах могут быть использованы: темп затухания силового переходного процесса; максимальное значение упругого момента в податливом звене и т. д.
Экспериментальными исследованиями в линии передач подъемников занимались следующие ученые: А. Н. Голубенцев [13], Н. Г. Гаркуша [44, 45], В. И. Дворников [15, 45], Л. В. Колосов [44, 46], В. В. Безпалько [46], А. П. Нестеров [32–34], В. М. Чермалых [47], Н. В. Середа [48], В. Д. Белый [49] и др.
Колебательные процессы в элементах подъемников можно наблюдать на осциллограммах промышленных экспериментов (рис. 1) [50].
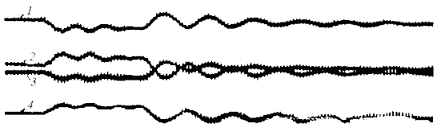
Рис. 1 – Осциллограмма аварийной остановки клетей в середине ствола многоканатной подъемной установки
Из рис. 1 видно, что во время аварийной остановки в четырех канатах 1, 2, 3, 4 возникают колебательные процессы, которые продолжаются после остановки машины и со временем затухают.
На рис. 2 приведены упругие моменты, которые имеют колебательный характер при пуске и остановке асинхронного двигателя [13, 50].
На осциллограмме (рис. 3) представлены переходные процессы в многоканатных подъемных машинах шахт Кривбасса с двигателями постоянного тока при нормальных эксплуатационных режимах [50].
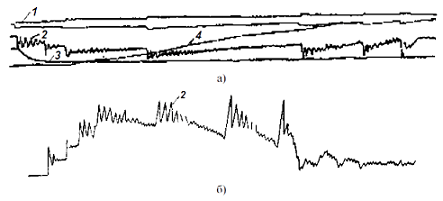
Рис. 2 – Осциллограммы переходных процессов в подъемной машине с асинхронным электродвигателем: 1 – ток статора электродвигателя; 2 – упругий момент на выходном валу редуктора; 3 – усилие в тормозной тяге; 4 – угловая скорость двигателя.

Рис. 3 – Осциллограммы переходных процессов в многоканатных подъемных машинах шахт Кривбасса с двигателями постоянного тока: 1 – ток якорной цепи двигателя; 2 – перемещение корпуса подпружиненного редуктора; 3 – скорость вращения органа навивки; 4 – упругий момент на выходном валу редуктора; 5 – напряжение якоря двигателя
Из рис. 3 видно, что для подъемных машин с электроприводом по системе Г-Д (генератор-двигатель) ток якоря двигателя изменяется по ступенчатому закону, что вызывает колебательные процессы в линии передач (рис. 3, б). Во время разгона и торможения динамические нагрузки носят интенсивный колебательный характер. На других подъемных машинах (рис. 3, а и 3, в) колебательные процессы незначительные.
В работе [50] В. С. Ловейкин и А. П. Нестеров оценивают переходные процессы по таким критериям: удельные приведенные затраты, время цикла, эффективная мощность, быстрота затухания, коэффициент динамичности и рассматривают аналитические и численные методы синтеза оптимальных параметров, методы и направления оптимизации режимов движения подъемных машин. Авторы показывают, что применение демпфирующих устройств в линии передач подъемных машин силовых переходных процессов значительно поглотит энергию колебаний в валопроводе механической системы.
Выводы
В заключении отметим, что есть необходимость рассмотреть подъемники как многомассовые системы с невесомыми канатами, приводя массы канатов от узла колебания к близлежащим дискретным массам и системы, в которых учитывается масса канатов. На основе современной вычислительной техники возможно решать сложные динамические задачи подъемников как многомассовых механических систем с упруго-вязкими связями в процессе пуска и торможения подъемника с реальной характеристикой системы управления и тормозов при рабочих режимах работы и при остановке подъемных сосудов предохранительным торможением.
Список литературы
- Динник А. Н. Динамические напряжения в подъемном канате при внезапной остановке верхнего конца / А. Н. Динник. – Южный инженер. – 1917. – № 3–4.
- Федоров М. М. Методология динамической теории расчета подъемного каната вертикальных шахт / М. М. Федоров // Записки института горной механики. АНУССР. – 1936. – № 1.
- Флоринский Ф. В. Динамика шахтного подъемного каната / Федор Валентинович Флоринский. – М. : Углетехиздат, 1955. – 238 с.
- Савин Г. Н. Динамическая теория расчета шахтных подъемных канатов / Г. Н. Савин. – К. : Из–во АН УССР, 1949. – 238 с.
- Савин Г. Н. Динамика нити переменной длины / Г. Н. Савин, О. А. Горошко. – К. : Из–во АН УССР, 1949. – 332 с.
- Шахтный подъем: Научно-производственное издание / В. Р. Бежок, В. И. Дворников, И. Г. Манец, В. А. Пристром ; общ. ред. Б. А. Грядущий, В. А. Корсун. – Донецк : ООО «Юго-Восток Лтд», 2007. – 624 с.
- Степанов А. Г. Динамика шахтных подъёмных установок / Анатолий Григорьевич Степанов. – Пермь : УрО РАН, 1994. – 263 с.
- Мищенко Р. Л. Динамика и надежность стальных канатов с учетом внутреннего трения / Р. Л. Мищенко // Труды Одесского политехнического университета: научный и производственно-практический сборник по техническим и естественным наукам. Вып. I. – Одесса, 1997. – C. 106-109.
- Тимошенко С. П. Колебания в инженерном деле / С. П. Тимошенко, Д. Х. Янг, У. Уивер ; пер. с англ. Л. Г. Корнейчука. – М. : Машиностроение, 1985. – 472 с.
- Стретт Дж. В. (лорд Рэлей). Теория звука / Дж. В. Стретт (лорд Рэлей). – М. : Гостехиздат, 1955. – 318 с.
- Кожевников С. Н. Динамика машин с упругими звеньями / Сергей Николаевич Кожевников. – К. : Из-во АН УССР, 1961. – 160 с.
- Голубенцев А. Н. Динамика машин с упругими связями: дис … д–ра техн. наук / А. Н. Голубенцев. – Днепропетровск, 1956. – 454 с.
- Голубенцев А. Н. Динамика переходных процессов в машинах со многими массами / Александр Николаевич Голубенцев. – М. : Машгиз, 1959. – 146 с.
- Федорова З. М. Подъемники : учеб. пособие для машиностроит. спец. вузов / З. М. Федорова, И. Ф. Лукин, А. П. Нестеров. – К. : Вища шк., 1976. – 294 с.
- Дворников В. И. Теоретические основы динамики шахтного подъемного каната / В. И. Дворников, Е. Р. Къерцелин. – София, МОНТ, 1997. – 363 с.
- Артоболевский И. И. Динамические критерии режима движения машин / И. И. Артоболевский – Теоретична и приложена механика (Болгария). – 1974. – № 1. – С. 11-24.
- Михайленко Ф. Ф. Исследование и оптимизация динамических процессов в машинах: дис … канд. техн. наук / Ф. Ф. Михайленко. – Харьков, 1974. – 110 с.
- Назаров Л. В. Динамика пневмоколесних землеройно–транспортных машин: автореф. дис … д–ра техн. наук. / Л. В. Назаров. – Харьк. гос. автомоб.–дор. ун–т., Харьков, 1977. – 49 с.
- Фурунжнев Р. И. Проектирование оптимальных виброзащитных систем / Р. И. Фурунжнев. – Минск : Выш. шк., 1971. – 312 с.
- Хитрик В. Э. Методы динамической оптимизации механизмов, машин, автоматов / В. Э. Хитрик. – Л. : Изд-во ЛГУ, 1974. – 116 с.
- Холодов А. М. Основы динамики землеройно-транспортных машин / А. М. Холодов. – М. : Машиностроение, 1968. – 156 с.
- Вульфсон И. И. Виброактивность приводов машин разветвленной и кольцевой структуры / И. И. Вульфсон. – Л. : Машиностроение, 1986. – 104 с.
- Коловский М. З. Автоматическое управление виброзащитными системами / М. З. Коловский. – М. : Наука, 1976. – 220 с.
- Троицкий В. А. Оптимальные процессы колебаний механических систем / В. А. Троицкий. – Л. : Машиностроение, 1976. – 248 с.
- Калгаев В. А. Оптимизация параметров ходовых частей железнодорожного подвижного состава / В. А. Калгаев. – М. : Машиностроение, 1980. – 215 с.
- Лазорян В. А. Устойчивость движения рельсовых экипажей / В. А. Лазорян, Л. А. Лугач, М. Л. Коротенко. – К. : Наук. думка, 1972. – 196 с.
- Ловейкин В. С. Оптимизация режимов движения механизмов грузоподъемных машин для транспортирования пассажиров / В. С. Ловейкин // Подъемн.-трансп. оборуд.: респ. межвед. науч.–техн. сб. – К., 1991. – Вып. 22. – С. 9-14.
- Кожевников С. Н. Оптимизация переходного процесса во времени затухания в подъемном лифте / С. Н. Кожевников, П. М. Совов // Механика машин. – 1971. – Вып. 39-40. – С. 18-21.
- Совов П. М. Исследование переходных процессов в механизмах подъема лифтов: дис … канд. техн. наук / П. М. Совов. – К., 1972. – 120 с.
- Федоров М. М. Метод определения наивыгоднейшего за раз поднимаемого груза для вертикальных шахт / М. М. Федоров // Избранные труды: В 2 т. – К.: Изд-во АН УССР, 1957. – Т.2. – С. 167-187.
- Федоров М. М. Теория гиперболо–функционального рудничного подъема / М. М. Федоров // Избранные труды: В 2 т. – К.: Изд-во АН УССР, 1957. – Т. 1. – С. 133-192.
- Нестеров А. П. Оптимизация силовых стационарных процессов шахтных подъемных установок / А. П. Нестеров; Ин-т геотехн. механики АН УССР. – Днепропетровск : [б. и.], 1977. – 19 с.
- Нестеров А. П. Оптимизация силовых процессов и параметров шахтных подъемных установок : дис. ... д-ра техн. наук / А. П. Нестеров. – Днепропетровск, 1987. – 521 с.
- Нестеров А. П. Оптимизация параметров шахтных подъемных установок по быстроте затухания силового переходного процесса / А. П. Нестеров, А. М. Дроговоз, С. Н. Вахнин // Динамика и прочность горных машин. – 1976. – Вып. 4. – С. 4-9.
- Нестеров А. П. Оптимизация режимных и грузовых параметров шахтного подъемника / А. П. Нестеров // Подъемно-транспортное оборудование: респ. межвед. науч.– техн. сб. – К., 1990. – Вып. 21. – С. 26-28.
- Давыдов Л. Б. Вариационные методы теории рудничного подъема / Л. Б. Давыдов. – М. : Металлургиздат, 1953. – С. 315-350.
- Левин Б. Я. К вопросу о наивыгоднейшем динамическом режиме рудничного подъема / Б. Я. Левин, С. Б. Браиловский – М. : Металлургиздат, 1953. – С. 214-306.
- Чермалых В. М. Исследование оптимальных по динамичности систем подъема глубоких шахт: дис … д-ра техн. наук / В. М. Чермалых. – Днепропетровск, 1970. – 420 с.
- Масляный А. С. Исследование рациональных динамических режимов работы многоканатных подъемных установок: дис … канд. техн. наук / А. С. Масляный. – Днепропетровск, 1962. – 230 с.
- Гамаюнов В. В. Исследование и разработка режимных параметров подъема с асинхронным вентильным каскадом: автореф дис … канд. техн. наук / В. В. Гамаюнов. – Харьков, 1981. – 26 с.
- Ловейкин В. С. Определение оптимальных режимов движения механизмов грузоподъемных машин / В. С. Ловейкин // Подъемно-трансп. оборуд. : респ. межвед. науч.– техн. сб. – К., 1987. – Вып. 18. – С. 31-35.
- Еланчик Г. М. Рудничные подъемные установки / Г. М. Еланчик. – М. : Госгортехиздат, 1941. – 648 с.
- Федорова З. М. Метод расчета оптимальных режимов управления шахтных скиповых подъемных установок / З. М. Федорова, В. В. Гамаюнов // Прочность и долговечность горных машин. – М.: 1979. – Вып. 5. – С. 147-152.
- . Гаркуша Н. Г. Экспериментальное исследование действующих усилий в шахтных подъемных канатах / Н. Г. Гаркуша, А. Н. Черныш, Л. В. Колосов, В. Е. Артюхова // Стальные канаты. – К. : Техніка, 1967. – Вып. 4. – С. 26-29.
- Гаркуша Н. Г. Исследование переходных процессов в нелинейной системе «подъемная машина-канаты-грузы» / Н. Г. Гаркуша, В. И. Дворников, В. А. Костюченко // Стальные канаты. – К. : Техніка, 1968. – Вып. 5. – С. 23-26.
- Вертикальный транспорт на горных предприятиях / В. Н. Потураев, А. Г. Червоненко, Л. В. Колосов, В. В. Безпалько; под. общ. ред. проф. д-ра техн. наук В. Н. Потураева. – М. : Недра, 1975. – 351 с.
- Чермалых В. М. Исследование оптимальных по динамичности систем подъема глубоких шахт: дис … д–ра техн. наук / В. М. Чермалых. – Днепропетровск, 1970. – 420 с.
- Середа Н. В. Динамика упругих систем многоканатных шахтных подъемных установок: дис … канд. техн. наук / Н. В. Середа. – Харьков, 1981. – 169 с.
- Белый В. Д. Экспериментальное исследование динамических усилий в подъемных канатах на эксплуатационных подъемных установках / В. Д. Белый, К. К. Лесин // Вопросы горной механики. – М. : Углетехиздат, 1959. – С. 305-329.
- Ловейкин В. С. Динамическая оптимизация подъемных машин : монография / В. С. Ловейкин, А. П. Нестеров ; Восточноукр. нац. ун–т им. В. Даля. – Луганск : [б. и.], 2002. – 368 с.