Математическая модель нелинейных колебаний струны и отвеса каната мобильной подъемной установки

Аннотация

Ильин С. Р., Самуся С. В. Математическая модель нелинейных колебаний струны и отвеса каната мобильной подъемной установки Разработана математическая модель для исследования динамических процессов в струне и отвесе каната мобильной подъемной установки.

Проблема и ее связь с научными и практическими задачами.

Аварии на людских подъемах и в шахтных стволах вызвали практическую необходимость в создании нового вида спасательного оборудования – аварийно-спасательных мобильных подъемных установок с автономным энергоснабжением. В настоящее время в Украине создан головной образец мобильной подъемной установки АСППУ-6,3, который находится на вооружении оперативного отряда Государственной военизированной горноспасательной службы [1].

Сложности в применении таких установок заключаются в том, что все шахты имеют разные подъездные пути к стволу, иногда не позволяющие подъехать к копру на необходимое расстояние, а также различную систему отклоняющих шкивов. При временном размещении мобильной подъемной машины относительно копра (в отличие от стационарной установки) зачастую невозможно обеспечить значения углов девиации каната по отношению к отклоняющему шкиву в тех же допустимых пределах, что и для стационарной подъемной установки. Поэтому и параметры динамических отклонений каната в горизонтальной и вертикальной плоскостях по отношению к шкиву при торможении могут достигать значений, приводящих к выходу каната за реборды шкива и возникновению аварийной ситуации.

Это делает задачу определения допустимых значений геометрических параметров размещения оборудования мобильной установки (каната, его струны, отклоняющего шкива, машинного блока с тягачом), разработку и обоснование рациональных параметров системы торможения с учетом взаимовлияния динамических процессов в отвесе и струне каната при всех практически возможных вариантах применения в типовых шахтных условиях актуальной с научной и практической точек зрения.

Анализ исследований и публикаций.

Анализ известной литературы и документации по имеющейся подъемной установке АСППУ-6,3 и ее зарубежным аналогам показал, что их применение базируется на использовании положений, разработанных для стационарных подъемных установок. Поэтому, для определения степени применимости этих положений для мобильной установки необходимо провести обзор уже известных решений и выявить задачи, актуальные для мобильной установки и не имеющие до сих пор своего решения.

Для обеспечения безопасной работы мобильной подъемной установки во всех технически возможных производственных ситуациях на действующих стволах шахт и рудников необходимо знание основных зависимостей между амплитудно-частотными характеристиками пространственных продольно–поперечных колебаний наклонной струны головного каната и геометрическими, режимными и инерционными параметрами подъемной установки. Несмотря на достаточно большое количество исследований в этой области, проведенных для стационарных подъемных установок, ряд задач, характерных для мобильной установки, до сих пор не имеет решения.

Исследования в этой области проводились О. А. Горошко, Г. Н. Савиным, Ф. В. Флоринским, Л. В. Колосовым, В. И. Дворниковым, А. Н. Обуховым, Г. А. Трифановым и др. Но с усовершенствованием стационарных подъемных установок и появлением мобильной подъемной установки возникла необходимость в дополнительном исследовании их режимов торможения.

В работах [2–6] в математических моделях не учитывалось совместное взаимовлияние поперечных колебаний струны каната и продольных колебаний ветви каната. Отличительными особенностями мобильной подъемной установки являются большая длина струны по отношению ко всей длине каната и малая масса клети. При таких параметрах взаимовлияние продольных и поперечных колебаний может быть существенным, и поэтому необходимо построить модель, учитывающую их взаимосвязь.

Постановка задачи.

В связи с вышесказанным имеет научную и техническую актуальность разработка методики определения предельно допустимых геометрических параметров размещения мобильной подъемной машины относительно копра при проведении аварийно-спасательных работ в шахтных стволах. Для этого необходимо теоретически исследовать взаимовлияние колебаний наклонной струны каната и подъемного сосуда и разработать комплекс технических решений, направленных на обеспечение безопасной эксплуатации мобильных подъемных установок.

Изложение материала и результаты.

Для составления нелинейных дифференциальных уравнений продольно-поперечных колебаний наклонной струны и продольных колебаний отвеса каната одноконцевой ШПУ рассмотрим расчетную схему системы с распределенными параметрами, представленную на рис.1.

Исходные уравнения поперечных колебаний струны и продольных колебаний отвеса каната имеют вид:

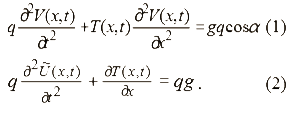
Выведем уравнение продольных колебаний отвеса со струной с учетом влияния поперечного динамического отклонения струны на продольные деформации каната. Рассматривая элемент dx каната, будем считать, что удлинение элемента dx в точке x состоит из суммы двух частей – удлинения U(x, t) вследствие чисто упругих продольных колебаний каната с концевым грузом и удлинения U_V(x, t), вызванного поперечным отклонением струны:

Соответственно, усилие в сечении каната

Как известно, длина дуги каната в сеченииxпри поперечных колебаниях равна

Учитывая, что величина V(x, t) для реальных параметров установок мала по сравнению с единицей, разложим подынтегральное выражение в степенной ряд и ограничиваясь двумя первыми членами первого порядка малости, получим:

Тогда, продольное удлинение каната U_V(x, t) на участке дуги в точке x, вызванное только его поперечными колебаниями с точностью до малых более высокого порядка будет равно

Подставляя (4)-(7) в (2) и выполнив необходимые преобразования, получим следующее нелинейное уравнение в частных производных, описывающее в первом приближении продольные колебания отвеса каната с учетом влияния поперечного отклонения струны:

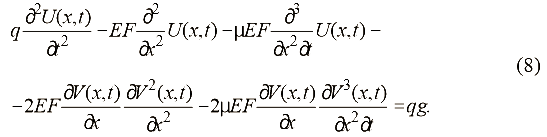
Вычислив производные в правой части (4) и подставив в (1), получим нелинейное уравнение поперечных колебаний струны каната

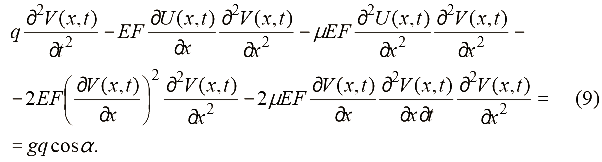
Уравнения (8) и (9) представляют собой систему нелинейных взаимосвязанных уравнений в частных производных, описывающих совместную динамику струны и отвеса каната подъемной установки с учетом их двустороннего влияния.

Учитывая сложность построения решения такой системы, для исследования ее основных динамических свойств построим дискретный динамический аналог рассматриваемой механической системы по методу, изложенному в монографии [7], расчетная схема которого представлена на рис. 2.

где: m_стр - приведенная масса динамического аналога струны; m_гр - приведенная масса динамического аналога отвеса каната с грузом.

Значения приведенных масс дискретного аналога найдем из условия равенства первых собственных частот поперечных и продольных колебаний звеньев дискретной и континуальной линейных систем, соответствующих исходной без учета влияния нелинейных эффектов.

Как известно, первая частота продольных колебаний континуального тяжелого каната с грузом на конце в первом приближении может быть определена по формуле Рэлея

где: Q – масса груза; q – масса единица длины струны.

Первая частота поперечных колебаний весомой струны, натянутой постоянной силой S, определяется по формуле:

тогда

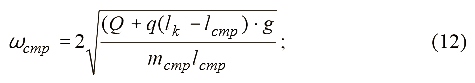
Используя принцип Даламбера, линейное дифференциальное уравнение свободных поперечных колебаний груза с приведенной массой струны m_стр имеет вид

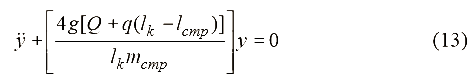
Следовательно, первая парциальная частота поперечных колебаний груза m_стр равна

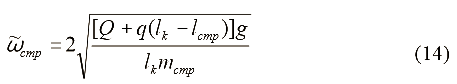
Из условия равенства парциальных частот найдем

Выведем нелинейную модель колебаний дискретного аналога для исследований в первом приближении амплитудно-частотных характеристик исходной системы и ее устойчивости.

На основании принципа Даламбера дифференциальные уравнения колебаний дискретной системы, представленной на рис. 2, имеют вид:

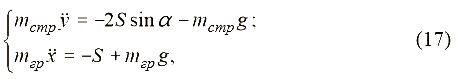
где х – упругое удлинение каната.

Вычислим Δx – упругое удлинение каната за счет поперечного отклонения груза m_стр.

Из рис. 2 видно, что

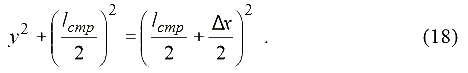
Пренебрегая членами порядка малости в первом приближении найдем

Подставив полученные выражения в дифференциальные уравнения (17), получим систему двух дифференциальных уравнений относительно x, y :

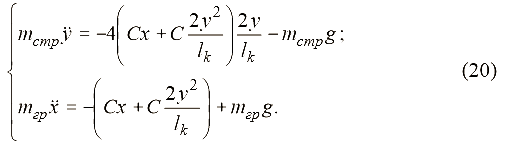
С учетом диссипации, пропорциональной скорости перемещения масс

где μ – коэффициент диссипации, получим аналогичную систему дифференциальных уравнений вида:

Решение системы (22) численным методом позволило установить наличие взаимовлияния динамических процессов в струне и отвесе каната и найти первые две зоны неустойчивости для разных соотношений длин струны и отвеса каната. На рис. 3 приведены графики продольных колебаний отвеса и поперечных колебаний струны каната для различных соотношений длин отвеса и струны.

Экспериментальные исследования взаимовлияния динамических процессов в струне и отвесе каната проводились на действующей подъемной установке при торможении в режимах спуска порожнего и подъема груженого подъемного сосуда в разных точках ствола.

На рис. 4 приведена осциллограмма вертикальных ускорений порожнего подъемного сосуда при аварийном торможении в середине ствола, где влияние массы струны при поперечных колебаниях уже достаточно существенно. Видно, что происходит явно выраженная модуляция вертикальных затухающих колебаний сосуда за счет периодической перекачки энергии поперечных колебаний струны в колебания сосуда и наоборот (режим биения) совпадающая с картинами продольных колебаний в первой и второй зонах неустойчивости, полученных из численных решений (рис. 3). Визуально режим биения такого же характера наблюдался авторами одновременно и на поперечных колебания струны. Координаты зоны активной перекачки энергии с достаточной точностью совпали с результатами расчета по приведенной модели.

Выводы и направление дальнейших исследований.

Результаты проведенных теоретических и экспериментальных исследований свидетельствуют о значительном взаимовлиянии динамических процессов в струне и вертикальном отвесе каната, которое наблюдается при совпадении частот продольных колебаний в отвесе каната и поперечных в его струне, а также при их двукратном соотношении.

Результаты дальнейших исследований позволят разработать рекомендации по обоснованию и выбору рациональных и безопасных режимов эксплуатации мобильных подъемных установок и длины струны для различных условий их применения на конкретных шахтных стволах.

Список источников.

1. Смоланов С. Н., Колесов О. А., Бондаренко В. И. и др. Аварийно-спасательная передвижная подъемная установка / Смоланов С. Н., Колесов О. А., Бондаренко В. И. и др. // Уголь Украины. – 2003. – №1 – С. 4-45. .
2. Колосов Л. В., Жигула Т. И. Продольно-поперечные колебания струны каната подъемной установки / Колосов Л. В., Жигула Т. И. // Известия вузов. Горный журнал. – 1981. – №3 – С. 83-86.
3. Флоринский Ф. В., Колосов Л. В., Обухов А. Н. О поперечных колебаниях струны подъемной установки / Флоринский Ф. В., Колосов Л. В., Обухов А. Н. // Стальные канаты. – Киев: Техника, 1971. – Вып.8. – С. 236-239.
4. Трифанов Г. Д. Поперечные колебания струны каната подъемной установки при предохранительном торможении / Трифанов Г. Д. // Известия вузов. Горный журнал. – 1984. – №2 – С. 74-77.
5. Колосов Л. В., Обухов А. Н. Предельная длина струны каната шахтной подъемной установки / Колосов Л. В., Обухов А. Н. // Известия вузов. Горный журнал. – 1976. – №11 – С. 128-132.
6. Бежок В. Р., Дворников В. И., Манец И. Г., Пристром В. А. Шахтный подъем./ Бежок В. Р., Дворников В. И., Манец И. Г., Пристром В. А. – Донецк: ООО «Юго-Восток, Лтд», 2007.– С. 53-62.
7. В. Н. Потураев, А. Г. Червоненко, Л. В. Колосов и др. Вертикальный транспорт на горных предприятиях / В. Н. Потураев, А. Г. Червоненко, Л. В. Колосов и др. – М.: Недра, 1975. – 351 с.