Принцип моделирования процесса формирования ЭДС отключенной обмотки статора двухскоростного асинхронного двигателя
Автор: Е. С. Дубинка, К. Н. Маренич
Источник: ХV Международная научно-техническая конференция Автоматизация технологических объектов и процессов. Поиск молодых
, г. Донецк, ДНР, 2015 г.
Аннотация
Дубинка Е. С., Маренич К. Н. Принцип моделирования процесса формирования ЭДС отключенной обмотки статора двухскоростного асинхронного двигателя. В статье рассматривается способ решения задачи моделирования трансформаторных ЭДС в отключенной обмотке двухскоростного асинхронного двигателя. Процессы, происходящие в этом двигателе, представлены как модель однофазного трансформатора при поочередном перекрытии его магнитной системы магнитопроводом. Приведены результаты моделирования, в результате которых были получены формы ЭДС с искажениями близкими к реально существующим, что свидетельствует о корректности полученной модели.
Двухскоростной асинхронный двигатель (АД) относится к базовым машинам электропривода скребковых конвейеров. Его применение позволяет осуществлять пуск конвейера с кратковременной ступенью пониженной скорости, а также реализовать доставочные операции на пониженной скорости.
Специфика эксплуатации этого двигателя в качестве базового элемента электропривода шахтных скребковых конвейеров дает основание считать его функциональной составляющей шахтного участкового электротехнического комплекса. Поэтому на него распространяются все требования в отношении электробезопасности эксплуатации и, прежде всего, положение ГОСТ 22929–78 [1]. В то же время, опыт эксплуатации двухскоростного АД позволил выявить наличие ЭДС в отключенных обмотках статора, что при отсутствии контроля цепи утечки в его силовых присоединениях создает потенциальную опасность электропоражения и требует дополнительных специальных исследований.
Предварительный анализ осциллограмм ЭДС отключенной обмотки статора работающего АД позволяет сделать выводы о существенном отличии ее по форме и частоте от соответствующих параметров номинального напряжения сети, о наличии совокупности высокочастотных и низкочастотных составляющих, что вносит свою специфику в процесс формирования тока и количества электричества в цепи утечки на землю [2].
Логично предположить, что процесс формирования ЭДС отключенной обмотки статора в значительной степени определяется конструктивными особенностями и динамическими характеристиками электромагнитной системы «статор – ротор» асинхронного двигателя.
Для выяснения функциональных возможностей аппаратов защиты от утечек тока на землю, в отношении выявления электрических параметров в присоединениях отключенной обмотки статора, научную и практическую актуальность представляет задача моделирования ЭДС указанной обмотки с учетом реальных параметров двигателя и питающей электрической сети (одна из статорных обмоток в этом случае включена в сеть).
В связи с этим, в качестве исходных данных модели следует учесть форму и геометрию пазов магнитопровода статора, особенности закладки и распределения в этих пазах статорных обмоток, величину воздушного зазора между магнитопроводом статора и ротора, форму и геометрию магнитопровода ротора и угловую скорость его вращения, как параметр, устанавливающий частоту перекрытия пазов статора магнитопроводящим материалом фрагментов магнитной системы ротора.
В обобщенной форме процессы, происходящие в двухскоростном двигателе, могут быть представлены моделью однофазного трансформатора при поочередном перекрытии его магнитной системы магнитопроводом, при этом частота перекрытий может меняться, что соответствует процессам при работе двигателя.
Рассмотрим простейший случай – процессы при поочередном перекрытии П–образного магнитопровода однофазного трансформатора магнитопроводящей средой. Схема замещения магнитной цепи трансформатора представлена на рисунке 1, где обозначено: F1, F2 – магнитодвижущие силы первичной и вторичной обмоток соответственно; Ф1, Ф2 – магнитные потоки; Фs – магнитный поток рассеяния; UM1, UM2 – падение магнитного напряжения на первичном и вторичном стержнях магнитопровода; Uzaz1 – магнитное напряжение воздушного зазора между первичным стержнем и ярмом, Uzaz2 – магнитное напряжение на воздушном зазоре между вторичным стержнем и ярмом; Uz1, Uz2 – магнитное напряжение на левой и правой половинах ярма.
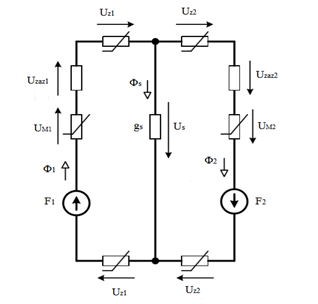
Рисунок 1 – Схема замещения магнитной цепи трансформатора
Составим математическое описание электромагнитной системы трансформатора [3]:
Магнитодвижущая сила первичной обмотки:

Магнитодвижущая сила вторичной обмотки:

Магнитный поток в цепи:

На всех участках магнитопровода напряженность магнитного поля H связана с магнитной индукцией B соотношением H = f(B), составляемым по таблице или графику намагничивания. В данной модели она задана таблично.
Структура компьютерной модели электромагнитной системы трансформатора представлена на рисунке 2. Работа схемы представленной на рисунке 2 заключается в следующем: первичная обмотка моделируемого трансформатора питается от блока e1, генерирующего синусоидальную ЭДС с заданной амплитудой и частотой. Блок Sub1 по второму закону Кирхгофа вычисляет индуктивную составляющую напряжения на зажимах первичной обмотки. Интегратор Integ, используя закон электромагнитной индукции в интегральной форме, вычисляет магнитное потокосцепление первичной обмотки согласно [4]:
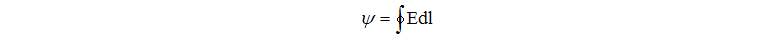
Магнитное потокосцепление поступает на пропорциональное звено с коэффициентом передачи 1/w1, вычисляющее магнитный поток в стержне с первичной обмоткой:

где w1 – количество витков первичной обмотки.
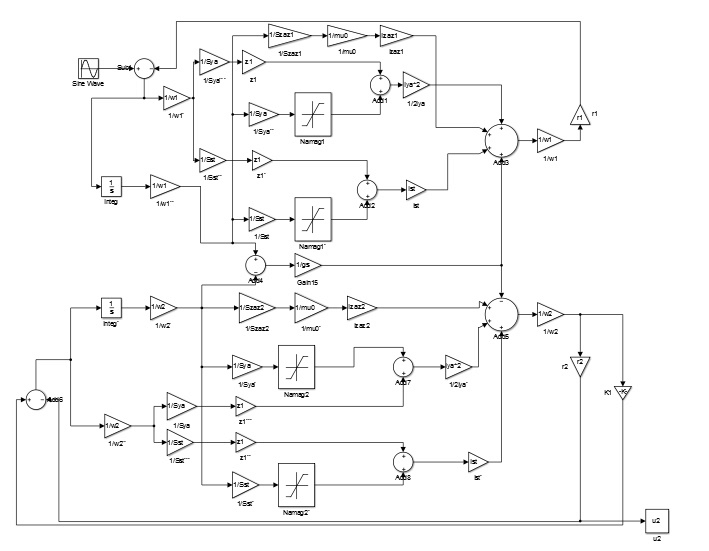
Рисунок 2 – Структура компьютерной модели электромагнитной системы трансформатора
Величина магнитного потока поступает на три пропорциональных звена: блок 1/Sst - вычисляет магнитную индукцию в первичном стержне; блок 1/Sya - вычисляет магнитную индукцию в левой половине ярма магнитопровода; блок 1/Szaz1 - вычисляет магнитную индукцию в зазоре между первичным стержнем и ярмом:
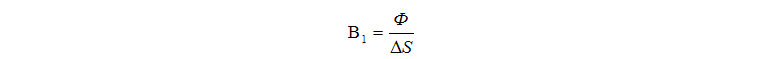
Напряжённость магнитного поля вычисляется исходя из:
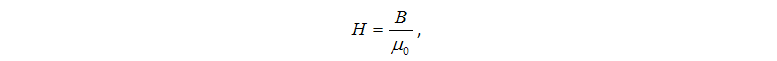
где μ0 = 4π×10-7 Гн/м – абсолютная магнитная проницаемость вакуума.
Сигнал индуктивной составляющей напряжения с сумматора Sub1 подаётся на пропорциональное звено с коэффициентом передачи 1/w1. Сигнал на выходе этого звена подаётся на два пропорциональных звена 1/Sst и 1/Sya, на выходе которых формируется скорость изменения магнитной индукции в первичном стержне и в левой половине ярма. Оба эти сигнала подаются на пропорциональные звенья с коэффициентом передачи z1, на их выходе формируются динамические составляющие напряжённости магнитного поля в первичном стержне и в левой половине ярма [5].
Сигналы магнитной индукции в первичном стержне и магнитной индукции в левой половине ярма подаются на нелинейные статические звенья Namag1 и Namag1`. На их выходе формируется статическая составляющая напряжённости магнитного поля в первичном стержне и в левой половине ярма соответственно. Сумматоры Add1 и Add2 складывают статическую и динамическую составляющие, и на их выходе формируется «полная» напряжённость магнитного поля в первичном стержне и в левой половине ярма.
Пропорциональное звено lst формирует падение магнитного напряжения на первичном стержне магнитопровода и через пропорциональное звено 1/2lya – суммарное магнитное напряжение на левой половине нижнего и верхнего ярма магнитопровода.
Сумматор Add4 вычисляет магнитный поток рассеяния трансформатора, который подаётся на пропорциональное звено с коэффициентом передачи 1/gs, на его выходе формируется магнитное напряжение между узлами магнитной цепи. Сигналы, подающиеся на сумматор Add_u1, на выходе формируют МДС первичной обмотки. Он подаётся на пропорциональное звено 1/w1, на выходе которого формируется ток первичной обмотки согласно:
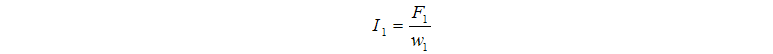
Сигнал тока первичной обмотки подаётся на пропорциональное звено r1, на выходе которого формируется напряжение на первичной обмотке:
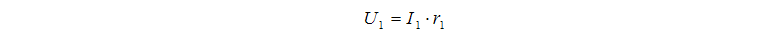
Величина напряжения на первичной обмотке вместе с ЭДС e1 подаётся на сумматор Sub1.
Процессы во второй половине модели аналогичны.
На рисунках 3–4 показаны осциллограмма напряжений на вторичной обмотке трансформатора.

Рисунок 3 – Осциллограммы напряжений на вторичной обмотке трансформатора при:
а) амплитуде 100В, частоте 70π рад/с, 50х25х50, k=1, Δ=0.09;
б) амплитуде 100В, частоте 200π рад/с, 50х25х50, k=1, Δ=0.09.
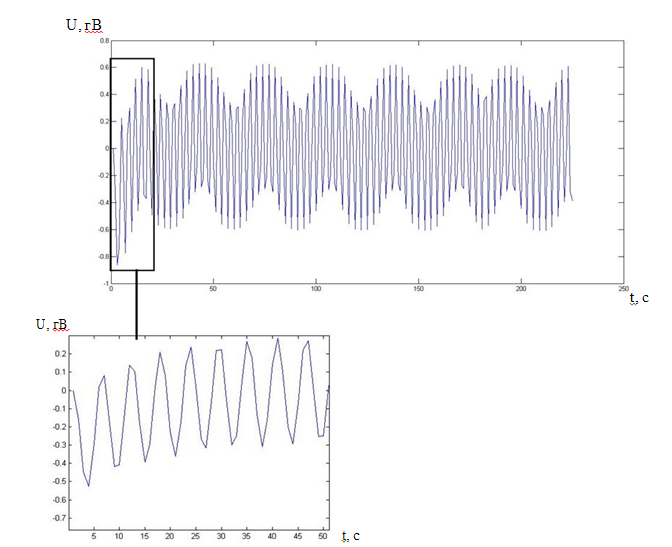
Рисунок 4 – Осциллограммы напряжений на вторичной обмотке трансформатора при амплитуде 50В, частоте 100π рад/с, 25х12х25, k=1, Δ=0.1
На основании исследования разработанной модели можно сделать вывод, что задание в частоте и очередности перекрытия воздушных зазоров магнитопроводящим материалом позволило получить формы ЭДС с искажениями близкими к реально существующим. Следовательно, данный подход может быть применен при исследовании уточненной модели двухскоростного асинхронного двигателя на основе представления его в виде совокупности трансформаторных компонентов.
Перечень ссылок:
- Правила технічної експлуатації електроустановок споживачів. Затв. 25.07.2006 № 258/ Міністерство палива та енергетики України. Х. Індустрія. 2007. – 272 с.
- Маренич К.М. Автоматичний захист електроустаткування шахт від аварійних станів і небезпек/К.М. Маренич, І.В. Ковальова // Навч. посіб. для вищ. навч. закл. Донецьк: ДВНЗ «ДонНТУ», 2013. – 199 с.
- Кацман М.М. Электрические машины / М.М. Кацман // Учебник для студентов вузов – М.: «Академия», 2001. – 463 с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи / Л.А. Бессонов // Учебник для студентов вузов – М.: «Высшая школа», 1996.
- Шмелёв В.Е., Дьякова О.С. Учебно-исследовательское моделирование однофазного трансформатора с учётом насыщения магнитной цепи/ Материалы Всероссийской НК «Проектирование инженерных и научных приложений в среде MATLAB». – Астрахань: Издательский дом «Астраханский университет», 2009. – с. 688–691.