Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і завдання дослідження, плановані результати
- 3. Модель автомата
- 4. Завдання аналізу впливу локальних перетворень на поведінки кінцевих автоматів
- 5. Приведення теоретичних результатів
- Висновки
- Список джерел
Вступ
Використання моделі кінцевих автоматів для опису різних дискретних систем і процесах є самим практичним методом їх подання. Однак для повного уявлення необхідно враховувати факт можливості впливу зовнішніх факторів, здатних змінити поведінку кінцевого автомата і всієї системи в цілому. Впливом можна вважати будь–яке локальне перетворення над вихідним станом автомата. З причини цього виникає необхідність провести аналіз поведінки двох станів автомата вихідного і перетвореного і порівняти їх. У даній роботі досліджується поведінки кінцевого автомата при локальних перетвореннях.
1. Актуальність теми
Модель кінцевого автомата може бути корисна при описі різних типів взаємодії об'єктів, як при технічних завданнях побудови керуючих систем, так і при завданнях опису поведінки будь–яких об'єктів, де потрібно вивчити поняття стан, впливу вхідного параметра і як результат – реакції на нього. Так теорія автоматів застосовується у розробці формальних мов і мов програмування, а також в програмуванні при безпосередньому написанні програм, в так званому автоматному програмуванні. У практичному сенсі реалізація кінцевого автомата є в будь–якому обчислювальному пристрої.
Тому актуальність дослідження моделі кінцевих автоматів очевидна, і як наслідок, важливо і дослідження поведінки кінцевого автомата при локальних перетвореннях.
2. Мета і завдання дослідження, плановані результати
Метою дослідження є розробка та дослідження методу оцінки впливу локальних перетворень на поведінку кінцевого автомата.
Основні завдання дослідження:
- Проаналізувати поведінку автоматів вихідного і породжуваного перетвореннями, отриманими через перекидання дуг.
- Оцінити ступінь близькості для будь перекидання дуг.
- Скласти опис структури класу локально породжених автоматів, розбиваючи його на підкласи автоматів, які будуть еквівалентні по мірі близькості їх поведінки поведінки початково заданого автомата.
Об'єкт дослідження: поведінки кінцевого наведеного автомата при локальних перетвореннях.
Предмет дослідження: знаходження ступеня близькості поведінки вихідного автомата і автомата, отриманого в результаті впливу локального перетворення у вигляді деякої послідовності перекидань дуг в графі переходів вихідного автомата.
3. Модель автомата
Проведемо порівняння поведінки автоматів при локальних перетвореннях, одержуваних у результаті перекидань дуг, візьмемо окремий випадок: в якості вихідного автомата будемо розглядати виразно діагностується близько k автомат, а під локальним перетворенням будемо розуміти перекидання рівно однієї дуги.
Автомат Мілі A = (S, X, Y, δ, λ, s0) буде використаний як ініціальний наведений ОД–k, в якому S – це кінцеве безліч станів, X, Y – кінцеві множини вхідних і вихідних, δ, λ – це функції переходів і виходів, і s0 прийнято за початковий стан. Індекс А чи значок штриха доданий до позначень цих об'єктів при необхідності для уникнення плутанини.
Автомат А називається виразно діагностуються автоматом порядку k, якщо k≥1 – найменше ціле таке, що для будь–якого вхідного слова p довжини k і будь–якої пари різних станів s, t∈S виконується нерівність λ (s, p) ≠ λ'(t, p).
Еквівалентними називаються два стани s і t одного і того ж автомата A або двох різних автоматів A і B відповідно, якщо для будь–якого вхідного слова р∈X * буде виконана умова λ (a, p) = λ'(b, p), де λ'– функція виходів автомата A або B. Наведений автомат називається таким чином за умови, якщо всі його стану попарно нееквівалентний.
Функції δ і λ поширюються звичайним чином на безліч X* всіх вхідних слів кінцевої довжини в автоматі.
Нехай w = (p, q) – вхід–вихідна слово, воно породжується станом s автомата А, якщо λ(s, р) = q. Довжина слова w буде позначена |w|.
Для кожного станом s у відповідність поставимо безліч λs всіх вхід–вихідних слів, які породжуються попарно нееквівалентними станами автомата. Поведінка автомата А будемо розумітися під безліччю λs0 вхід–вихідних слів, які породжуються його початковим станом.
Найбільш зручним буде задати автомат у вигляді графа переходів, у якого вершини будуть відповідати станам з S, а дуги будуть четвірками (s, x, y, t), при t = δ(s, x), y = λ(s, x). Відміткою дуги називається пара (x, y), початок дуги – s, кінець дуги – t. При e = (t, x, y, u) – дуга в графі переходів автомата A, перекидання цієї дуги зі стану u в стан v, відмінне від u, називатиметься заміною її наступної дугою – (t, x, y, v) .
4. Завдання аналізу впливу локальних перетворень на поведінки кінцевих автоматів
Дослідження автомати, близьких по поведінці в тому чи іншому сенсі, а також структура їх класів [1], триває досить давно, в основному завдяки розвитку теорії експериментів з автоматами. Підстава теорії експериментів з автоматами було покладено Муром [12], тоді був вперше запропонований алгоритм визначення еквівалентності автоматів.
Роботи А. Гілла [1], Ф. Хенні, М.П. Василевського, A.M. Богомолова [10], І.С. Грунського [2 , 3 , 8], С.В. Яблонського, І.К. Рисцова, Н.В. Євтушенко, В.А. Твердохлебова, А.Ф. Петренко, а також багатьох інших присвячені теорії експериментів.
Зараз теорія експериментів продовжує і далі своє інтенсивний розвиток серед наукових діячів, при дослідженні впливу локальних перетворень на поведінки автоматів, отримано важливі результатів. Саме вплив перекидань дуг на графі переходів автомата на поведінку автомата наведено в [3–7 , 9]. Вивчивши ці роботи, виявлені такі висновки:
- у наведеному автоматі перекидання рівно однієї дуги завжди викликає зміну поведінки автомата, яке стає нееквівалентним вихідного наведеним автомату;
- при перекиданні однієї дуги завжди виходить неізоморфних автомат;
- при перекиданні двох дуг може вийти автомат, еквівалентний вихідному;
- при перекиданні двох дуг вхідні–вихідні позначки на перекинутих дугах повинні збігатися;
- перекидання більше двох дуг можлива, за умови, коли вхідні–вихідні позначки на перекинутих дугах різні;
- існує така структура автоматів, де в графах автоматів, які мають не досить сильні зв'язки, до можлива перекидання ≥ 2 дуг;
- при здійсненні ≥ 4–х перекидань в деяких існуючих сильно пов'язаних автоматах зберігається ізоморфізм;
- перекидання дуг, що зберігає ізоморфізм, можлива в автоматах, що володіють певною симетрією графа переходів, яка відбивається і в циклічній структурі графа;
- зберігати ізоморфізм при перекиданні дуг можуть автомати, які володіють певною симетрією графа переходів, що відбивається і в циклічній структурі графа.
5. Приведення теоретичних результатів
Розглянемо структуру локально породженого класу. Наступна теорема показує, як пов'язано відстань між двома локально породженими автоматами і два параметри: d – довжина найкоротшого слова, яке переводить автомат з початкового стану в стан з якого буде перекинута дуга, і k – параметр ОДk–автомата.
Теорема 5.1. Нехай А – ініціальний наведений ОД–k–автомат і A' отриманий з А перекиданням дуги (t, x, y, u) у стан v. Тоді ρ (A, A') ≥1 / (d + k + 1), де d – довжина найкоротшого вхідного слова w такого, що δ (s0, w) = t.
Доказ. Щоб відрізняти стану автомата А від станів A', будемо стану останнього позначати штрихом і пару (s, s') називати подвійними, де s∈S, s'∈S '. Покажемо спочатку, що стану u і v 'помітні деяким словом довжини, що не більшою k. Для цього скористаємося прийомом, використаним при доказі того факту, що перекидання дуги в будь–якому наведеному автоматі завжди призводить до автомата, що не ізоморфного вихідного [7]. Побудуємо автомат В, рівний прямий сумі автоматів А і А', і розглянемо процес побудови Рi–таблиць [11] для автомата В.
Оскільки таблиці виходів автоматів А і А 'збігаються, то в таблиці Р1 кожен клас еквівалентності складається з пар двоїстих станів.
Зауважимо, що будь–яка пара (s, s'), крім пари (t, t'), з будь–якого х знову переходить в пару двоїстих станів. Пара (t, t')
– єдина, для якої це не виконується, оскільки δB (t, x) = u і δB (t', x) = v'. Звідси випливає, що поки стану (t, t') k–еквівалентні,
будь–яка пара (s, s'), відмінна від (t, t'), буде (k + 1) –еквівалентной. Сама ж пара (t, t') k–еквівалентна, поки пара (u, v')
є (k–1) –еквівалентной. Але, якщо (u, v') (k–1) –еквівалентна, то тоді пари (t, t'), (u, u'), (v, v') k–еквівалентні
і, значить, стану u, u', v, v' належать одному класу еквівалентності в таблиці Рk. Так як А ОД–k–автомат, то для деякого
i Нехай тепер w – найкоротша вхідне слово в автоматі А, що переводить його з початкового стану в стан t, і р – найкоротша
слово, розрізняє u і v'. Нехай |w| = d, |p| = i, і як показано вище, i≤k. Ясно, що в автоматі А 'δ (s'0, w) = t'. Тоді δ (s0, wx) = u,
δ (s'0, wx) = v', λ (s0, wx) = λ (s'0, wx), але λ (s0, wxp) ≠ λ (s' 0, wxp), причому | wxp | ≤d + 1 + k, що потрібно було довести. Покажемо, що отримана оцінка відстані досяжна. На малюнку 5.1 наведено ініціальний автономний автомат А. Нехай автомат А 'є результатом
перекидання однієї дуги в автоматі А: дуга (6,0,2,5) перекидається в стан 3 і замінюється дугою (6',0,2,3') . Оскільки перекидається дуга,
яка виходить із стану 6, то найкоротший слово w має довжину d = 3. Легко бачити, що λ (s0,0000) = λ (s'0,0000), але λ (s0,00000) ≠ λ (s'0,00000).
Тому wxp = 00000 і |wxp| = 5. Звідси ρ (A, A') = 1/5. На прикладі видно, що в результаті перекидання дуги автомат A 'став наведеним автоматом,
так як стану 5 і 6 стали еквівалентними. Рисунок 5.1 – Приклад перекидання однієї дуги в автоматі ОД–2 Теорема 5.2. Нехай А – ініціальний наведений автомат і A'отриманий з А перекиданням дуги (t, x, y, u) у стан v.
Тоді ρ (A, A ') ≥1 / (d + n), де d – довжина найкоротшого вхідного слова w такого, що δ (s0, w) = t. Теорема 5.3. Клас K i (A) складається з усіх тих автоматів А', для яких виконується така умова: d + з + 1 = i. Повний доведення теореми 5.2 та теореми 5.3 буде приведено у тексті магістерської роботи. У даній роботі були отримані такі результати: При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2015 року. Повний текст роботи та
матеріали по темі можуть бути отримані у автора або його наукового керівника після зазначеної дати.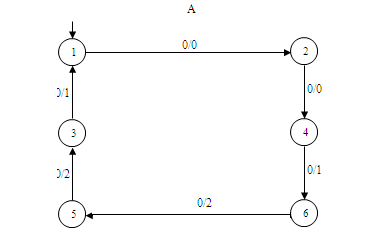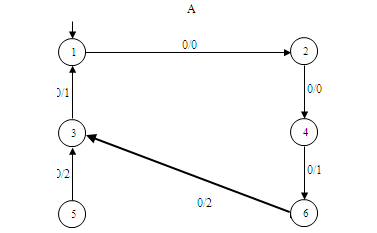
(анімація: 2 кадрів, 7 циклів повторення, розмір - 377×233, 5,22 кілобайт)Висновки
Список джерел
Дискретные модели в теории управляющих систем
. – М.: Макс–Пресс, 2009, C. 150–158.
