Об алгебре языков, представимых в графах с отмеченными вершинами

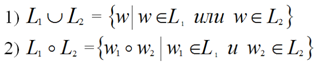
Автор: Пряничникова Е.А., Грунский И.С.
Источник: Грунский И.С. Об алгебре языков, представимых графами с отмеченными вершинами / И.С. Грунский, Е.А. Пряничникова / / Труды Ин-та прикл. математики и механики НАН Украины. – 2009. – т.18. – С. 37–46.

В докладе рассматриваются свойства алгебры языков, представимых ориентированными графами с отмеченными вершинами. Такие графы широко используются при построении вычислительных систем [1].

Пусть X – конечный алфавит, Х⁺ – множество всех непустых слов конечной длины в алфавите X. По аналогии с [2] введем на языках L₁, L₂ ∈ X следующие операции:

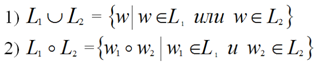
Операция º на множестве Х⁺ определяется следующим образом: для всех w₁, w₂ ∈ X , всех х,у ∈ X w₁x º yw₂=w₁xw₂, если х=у; w₁x º yw₂ – не определено, если х≠у.

Рассмотрим алгебраическую систему (2^x+, °, ∪, *, ∅, X). Регулярными выражениями в этой алгебре будем называть формулы:

1)∅ является регулярным выражением и представляет пустое множество.

2)Для каждого х∈Х символ х является регулярным выражением и представляет язык {х}.

3)Для каждого х∈Х и у∈Х ху является регулярным выражением, представляющим язык {ху}.

4)Если р и q – регулярные выражения, то выражения (р°),(p∪q), (p)^* также являются регулярными.

Множество 2^x+ является идемпотентным полукольцом относительно операций ° и ∪[2]. Для регулярных выражений в алгебре (2^x+, °, ∪, *,∅, X) выполняются следующие соотношения:

Теорема 1. В алгебре (2^x+, °, ∪, *,∅, X) уравнение с одним неизвестным вида Y = Y°R∪Q имеет наименьшее решение Y = R^*°Q∪Q .

Теорема 2. Для системы уравнений существует наименьшее решение, регулярное относительно коэффициентов R_ij и свободных членов Q_i.

Назовем графом с отмеченными вершинами четверку G=(Q, E,X, μ), где Q – конечное множество вершин, |Q|=n, E⊆QxQ – множество дуг, X-множество отметок вершин, μ:Q→X–функция отметок вершин. Пусть I⊆Q – множество начальных вершин графа, F⊆Q – множество финальных вершин. Путем в графе G будем называть конечную последовательность смежных вершин (q₁),(q₂),...,(q_k), где (q¹) (qⁱ⁺¹)⊆E. Отметкой пути будем называть р∈Х⁺ , такое, что р=μ(q₁) μ(q₂)...μ(q_k). Множество отметок всех путей в графе G, у которых начальная вершина q₁∈I, конечная вершина q_k∈F, назовем языком, порожденным графом G, и обозначим L(G). Для так называемых детерминированных графов с одним начальным состоянием свойства языков изучались в работе [3].

Теорема 3. Для языка L равносильны следующие утверждения: 1)Язык L представим в виде регулярного выражения алгебры (2^x+, °, ∪, *,∅, X). 2) Существует такой граф с отмеченными вершинами G, что L(G)=L.

СПИСОК ЛИТЕРАТУРЫ

1. Капитонова Ю.В. Математическая теория проектирования вычислительных систем / Ю.В. Капитонова, А.А. Летичевский – М: Наука, 1988. – 296 с.

2. Ginzburg А. Algebraic Theory of Automata / A. Ginzburg – Academic Press New York – 1968.

3. Grunsky I. Languages Representable by Ver-tex-labeled Graphs / I.Grunsky, O.Kurganskyy, I.Potapov – Proceedings of the 30th International Symposium on Mathematical Foundations of Computer Science, LNCS, v.3618, 2005, C. 435–446.