Вероятностный анализ индуктивных и рефлексивных утверждений
Автор: А.И. Андрюхин, С.Д. Подтынный
Источник: Информационные управляющие системы и компьютерный мониторинг (ИУС КМ – 2015) – 2015 / Материалы VI международной научно-технической конференции студентов, аспирантов и молодых ученых. — Донецк, ДонНТУ — 2015.
Аннотация
А.И. Андрюхин, С.Д. Подтынный Вероятностный анализ индуктивных и рефлексивных утверждений. Рефлексивные связи рассматриваются, как обратные связи в нейроморфных сетях. Анализ парадоксальных высказываний при применении вероятностной логики с ее более мощным алфавитом, нежели булева логика приводит к исчезновению противоречивых свойств суждений. Приведены расчеты для стационарных вероятностей рефлексивных связей в базовых индуктивных утверждениях.
Введение
Впервые вероятностная логика (ВЛ) для построения надежных технических систем использовалась в [1]. Активная роль вероятностной логики в исследованиях искусственного интеллекта [2–5].
В современной компьютерной индустрии известны аппаратные реализации PCMOS вероятностных комплементарных металлоксидных полупроводников
(Probabilistic Complementary Metal-Oxide Semiconductor) [6]. В ней определение возможности события, ранее требовавшее множества транзисторов, сводится к операции в одном или нескольких вентилях, в которых входные и выходной сигналы — вероятности.
Модель считают рефлексивной, если в ней отражена способность строить модели себя и других систем и одновременно видеть себя строящими такие модели. Рефлексия всегда привлекала внимание специалистов различных научных направлений, так как по мнению многих известных специалистов, человека отличает от животного уровень ее развития. Поэтому выполнялись исследования рефлексии с различных точек зрения и в различных областях применения [7–11].
Целью исследования является оценка возможностей синтетического направления, которое соединяет:
- известное направление построения надежных систем из ненадежных элементов [1];
- расширения булевой логики, в частности ВЛ и индуктивной логики;
- исследования рефлексивных связей как обратных связей в нейроморфных системах и определения и определения их стационарных значений для базовой модели индуктивной логики. .
Основными элементами вероятностной логики являются логические связки-операции(¬,∧,∨,↔,→) с индексом p, с помощью которого мы указываем вероятностную оценку истинности определенной формулы [4–6]. Пример: интерпретация вероятностного отрицания ¬p представлен в таблице 1.
Нужно отметить, что ВЛ не является дистрибутивной и ассоциативной. Общие сведения о свойствах и операциях ВЛ представлены на рисунке 1. Для этой таблицы справедливо r=pq + (1 − p)(1 − q).

Рисунок 1 — Свойства и операции ВЛ
Применение ВЛ для описания функционирования PCMOS-схем можно проиллюстрировать, анализируя основные примитивы этой технологии, из которых мы рассмотрим инвертор на рис. 3 с соответствующей таблицей на рисунке 1.
Вероятность правильной работы инвертора может быть определена выражением (erf-функция Лапласа).

Рисунок 2 — erf-функция Лапласа
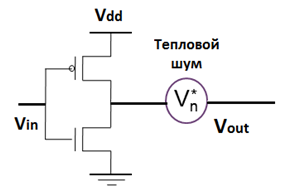
Рисунок 3 — МОП-инвертор
Рассмотрим одно из возможных применений ВЛ к известным научным проблемам взаимоотношений доказуемости, истинности, существования и над которыми работали Гедель, Россер, Смальян, Манин и др., на следующем примере. Можно показать, что при увеличении числа его предложений-фактов будем иметь базовую ситуацию индуктивного вывода с использованием рефлексивных рассуждений. Имеем 4 листа бумаги:
- Первый лист содержит три утверждения:
- X существует.
- X не существует.
- Все утверждения на этом листе ложны.
- Второй лист содержит утверждения:
- X существует.
- X не существует.
- Все утверждения на этом листе истинны.
- Третий лист содержит утверждения:
- X существует.
- X не существует.
- Одно из утверждений на этом листе ложно.
- Четвертый лист содержит утверждения:
- X существует.
- X не существует.
- Одно из утверждений на этом листе истинно.

Рисунок 4 — Рефлексивная модель трех представлений
Если действовать в рамках булевой логики, то представлены все возможные варианты. Пусть A,B,C,D,E — вероятностные оценки истинностей пяти предложений в каждом из 4 вариантов.
Можем построить следующие булевы соотношения для описания этих четырех случаев, где значения True(False) кодируются соответственно 1 (0):
I C = A(1 - A) / (1 + A(1 - A)
II C = 0
III Кубичное уравнение для С
A - A2 + (-4A + 6A2 - 4A3 + 2A4)C + (A - 4A2 + 7A3 - 6A4 + 3A5 - A6)C2 + (-A3 + 3A4 - 3A5 + A6)C3 = 0
IV Кубичное уравнение для С
1 - 2A + A2 + 2A3 - A4 + (-2 + 2A + 2A2 - 7A3 + A4 + 3A5 - A6)C + (A - 4A2 + 4A3 + 3A4 - 6A5 + 2A6)C2 + (A3 - 3A4 + 3A5 - A6)C3 = 0
Часть графиков действительных решений представлена на рис. 5.
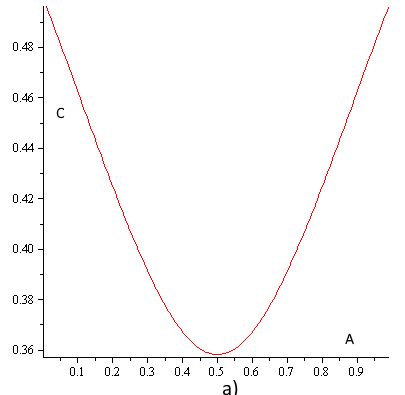
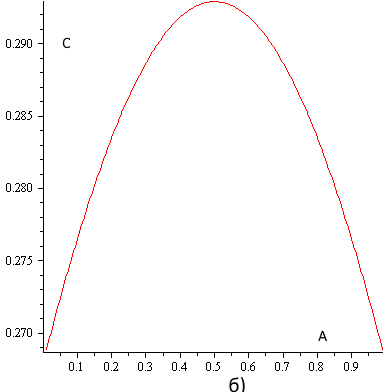
Рисунок 5 — a) зависимость С(А) в IV, b) зависимость С(А) в III
Выводы
Подчеркнем, что анализ парадоксальных высказываний при применении вероятностной логики с ее более мощным алфавитом, нежели булева логика приводит к исчезновению противоречивых свойств суждений [11]. Человек достаточно терпимо относится к наличию противоречивых суждений и это указывает на необходимость развития ВЛ при построении и представлению событий в нейроморфных системах.
Список использованной литературы
- Нейман Дж. Вероятностная логика и синтез надежных организмов из ненадежных компонент // Шеннон К. Э., Маккарти Дж. Автоматы Сборник статей. — Пер. с англ. — М.: Издательство иностранной литературы, 1956. — 403 с.
- Витяев Е. Е., Перловский Л. И., .Ковалерчук Б. Я., Сперанский С. О. Вероятностная динамическая логика мышления// Нейроин-форматика, 2011, том 5, № 1
- Налимов В. В. Вероятностная модель языка. М.: Наука, 1979, 303 с.,
- A.Darwiche. Modeling and Reasoning with Bayesian Networks. — New York, Cambridge University Press, 2009
- Pearl D. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference.- Morgan-Kaufmann, 1988
- Pinar Korkmaz,
Probabilistic CMOS (PCMOS) in the Nanoelec-tronics Regime
, PhD Thesis, Georgia Institute of Technology, December 2007. - Тейяр де Шарден П. Феномен человека. М., 2001.
- Д. Хофштадтер, Гедель, Эшер, Бах: эта бесконечная гирлянда. Самара, 2001, 752 с.
- Лепский В. Е., Зорина Г. И. Рефлексивное предприятие XXI века // Рефлексивные процессы и управление, № 2, 2005, том 5, c. 21–40
- Милль Д. С. Система логики силлогистической и индуктивной: Изложение принципов доказательства в связи с методами научного исследования. — М.: ЛЕНАНД, 2011. — 832 с.
- Андрюхин А. И. Оценка рефлексивных связей в вероятностной логике // Системный анализ в науках о природе и обществе, Донецк, Доннту,№ 1(4)-2(5)’2013, с. 75–80.