ФРАКТАЛЬНЫЙ АНАЛИЗ ФИНАНСОВЫХ РЫНКОВ
Автор: М.В. Прудский
Источник: Информационные системы и математические методы в экономике. – 2012. – № 5; URL: http://ismme.esrae.ru/119-331
Аннотация
М.В. Прудский. ФРАКТАЛЬНЫЙ АНАЛИЗ ФИНАНСОВЫХ РЫНКОВ. Рассмотрены основные свойства и природа фракталов, возможности их применения в повседневной жизни, а также преимущества фрактального подхода при моделировании финансовых рынков. Будут разобраны основные стохастические модели временных рядов и на примере курса доллара будет построена фрактальная ARIMA лог-приростов, определение которой будет основано на фрактальном R/S-анализе размерности графика курса доллара. Будет дана также интерпретация показателя Хёрста – результата R/S-анализа, позволяющего судить о возможности прогнозирования исследуемого финансового инструмента.
Изложение основного материала
В современном мире финансовые рынки привлекают довольно широкий общественный интерес. Круг людей, которые имеют дело с финансовой аналитикой, разнится от рядовых трейдеров, до аналитиков глобальных корпораций и государственных органов. Человечество давно интересуют законы поведения таких практически непредсказуемых объектов. Котировки акций, валютные курсы, цены на фьючерсы, опционы и прочие финансовые инструменты – это лишь малая часть того, на чём может заработать деньги квалифицированный человек. Существует множество способов анализа событий, происходящих на рынках. Это и технический анализ, и фундаментальный, и теория волн Эллиота, а также много различных менее известных методик. Но одна методика выделяется среди них своей простотой и оригинальностью – фрактальный анализ. Многие слышали о том, что такое фрактал, изучали в школах и университетах, видели простейшие одномерные и сложные дифференциальные многомерные фракталы, но мало кто знает об их истинной пользе. Изобретённые Мандельбротом, они нашли применение практически во всех сферах повседневной жизни. Фрактальную природу имеют форма раковины моллюска, турбулентные завихрения в воздухе, человеческие сосуды, крона дерева, форма листа, волны, береговая линия, трещины, молнии и многие другие всем знакомые объекты реального мира. Фрактальную природу имеют и графики котировок акций и валют[1; 3]. Если вычислить фрактальные свойства времени и пространства финансовых инструментов, становится возможным осуществлять точечные и интервальные прогнозы будущих значений с высокой точностью. Фракта?л (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, т.е. составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Фактически не существует точного определения термина «фрактал». Бенуа Мандельброт, отец фрактальной геометрии, тоже не сформулировал точного определения. Фракталы имеют определенные особенности, которые измеримы, и свойства, которые являются желательными для целей моделирования. Первое свойство – самоподобие. Оно означает, что части в некотором роде связаны с целым. Это свойство самоподобия делает фрактал масштабно-инвариантным. Фрактальные зависимости имеют вид прямой на графиках, где обе оси имеют логарифмический масштаб. Модели, описываемые таким образом должны использовать степенную зависимость (вещественное число, возведенное в степень). Эта особенность масштабирования по степенному закону является вторым свойством фракталов, фрактальной размерностью, которая может описывать либо физическую структуру, такую как легкое, либо временной ряд [3]. Слово «фрактал» может употребляться не только как математический термин. Фракталом в прессе и научно-популярной литературе могут называть фигуры, обладающие какими-либо из перечисленных ниже свойств:
1. Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур
(таких как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент
регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала
увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную
картину.
2. Является самоподобной или приближённо самоподобной.
3. Обладает дробной метрической размерностью или метрической размерностью, превосходящей
топологическую.
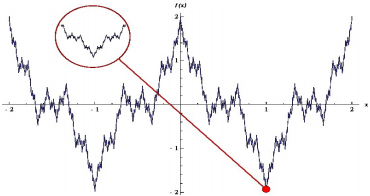
Рисунок 1 – Пример фрактала
Фракталы – безусловно красивые математические причуды природы. Если взглянуть на график функции Вейерштрасса, то можно увидеть сходство с графиками курсов валют или котировок акций. Этот фрактал описывается функцией
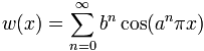
где a – нечётное число, а b – число, меньшее единицы. Эта функция непрерывная и нигде не дифференцируемая. Применяется для моделирования временных рядов методом Монте-Карло [9].
Стохастические модели временных рядов
Существует несколько процессов с кратковременной памятью, которыми обычно пользуются при
прогнозировании цен на финансовых рынках. В их числе:
1. AR.
2. MA.
3. ARMA.
4. ARIMA.
5. ARFIMA.
Остановлюсь более подробно на фрактальной авторегрессии.
ARIMA ARIMA (англ. autoregressive integrated moving average) – интегрированная модель авторегрессии — скользящего среднего – модель и методология анализа временных рядов, иногда называемые моделями (или методологией) Бокса-Дженкинса. Модель ARIMA(p,d,q) означает, что разности временного ряда порядка подчиняются модели ARMA(p,q) [4].
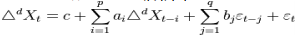
С использованием лагового оператора модель можно записать в таком виде:
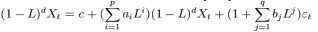
Модели ARFIMA Данные модели предполагают использование дробных порядков разностей, поскольку теоретически порядок интегрированности d временного ряда может быть не целой величиной, а дробной. В этом случае говорят о дробно-интегрированных моделях авторегрессии –скользящего среднего (ARFIMA, AutoRegressive Fractional Integrated Moving Average). Для понимания сущности дробного интегрирования необходимо рассмотреть разложение оператора взятия d-ой разности в степенной ряд по степеням лагового оператора для дробных d (разложение в ряд Тейлора):
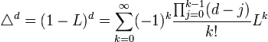
Кроме коэффициент при k-м члене ряда Тейлора = Гk-dГk+1Г-d. К полученным разностям применяется модель ARIMA. Таким образом, последняя модель является более точной в силу её фрактальных свойств [6].
R/S-анализ курса доллара к рублю. Прежде чем моделировать ряд курсов доллара, необходимо вычислить его фрактальную размерность. Для этого следует воспользоваться методикой R/S-анализа и вычислить показатель Хёрста. Для выполнения всех необходимых вычислений автором были использованы пакет статистического анализа «R 2.5.1», а также аналитический комплекс «Прогноз 5.26». Первым шагом станет преобразование исходного ряда в ряд лог-приростов, в дальнейшем все операции по моделированию будут происходить именно в отношении преобразованного ряда. На Рис. 2 можно увидеть преобразованный ряд.
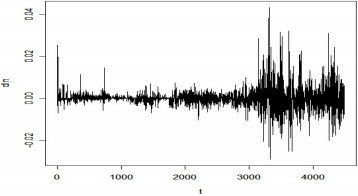
Рисунок 2 – Лог-приросты курса доллара
На этом рисунке особенно видна хаотичность показателя в кризисный и послекризисный периоды. Однако на данном этапе при применении R/S-анализа можно столкнуться с серьёзной трудностью – данная методика требует независимости данных во времени. Известен факт, что дневные данные по курсам финансовых инструментов обладают очень высокой автокорреляцией первых порядков. Коррелированно может быть до 7-10 значений. Для устранения этой проблемы применяется методика вычисления AR(1)- разностей. Конечно, метод разностей первого порядка не устраняет всю линейную авторегрессионную зависимость и не учитывает разности более высоких порядков, но он позволяет свести её к минимуму, достаточному для применения анализа с начальным условием независимости. Внешне ряд лог-приростов, скорректированный на AR(1)-разности, почти ничем не отличается от исходного ряда, однако его автокорреляция значительно ниже. Для вычисления фрактальной размерности ряда было использовано 4500 значений курса рубля к доллару с начала его публикации Центральным банком России. С имеющимся в распоряжении рядом связано несколько трудностей: 1. До 2002 года (включительно) Центральный банк Российской Федерации фиксировал значения курса только до 2-го знака после запятой, что создавало ошибки и неточности округления. 2. Курс доллара динамически изменяется в течение дня и иногда округление создаёт фиксацию на одинаковом курсе в течение нескольких дней. (особенно актуально для предыдущего недостатка). Вследствие перечисленных проблем возникают целые последовательности нулевых лог-приростов в ряду значений. Наибольшая такая цепочка была обнаружена ближе к концу исследуемого периода – она составила 10 значений. Для проведения анализа необходимо было разбить ряд скорректированных лог-приростов на несколько групп рядов меньшей длины. Далее посчитать в каждой группе рядов R/S-статистику и усреднить на количество элементов. Длину необходимо постоянно увеличивать до половины начального ряда. Авторы советуют не брать длину меньше 10, поскольку она может исказить значение RS-статистики [5]. В Таблица представлены результаты R/S-анализа курса доллара.
Таблица 1 - Результаты R/S-анализа/
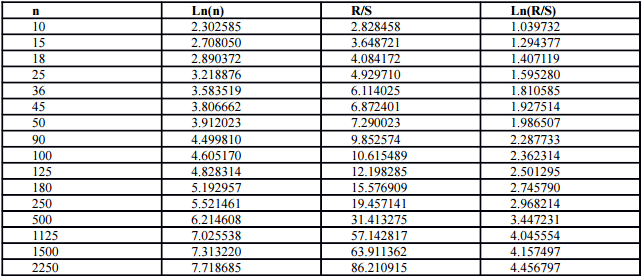
Таким образом, первоначальными данными для регрессии и определения фрактальной размерности станут 2-й и 4-й столбцы Таблица . Для того чтобы узнать размерность ряда, необходимо решить уравнение, прологарифмировав его: RS=nH•ec В итоге искомая регрессия будет иметь вид lnRS=c+H•lnn. Решением этой регрессии будут следующие значения: С = -0.4617; H = 0.6294; R 2 полученной регрессии составляет 0.997529, что свидетельствует о высокой точности и правдоподобности полученных результатов. На Рис. 3 представлен график R/S-статистик и регрессии по шкале у. По шкале х показан логарифм длины подпериода (n).
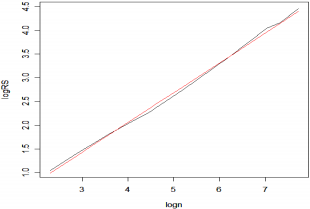
Рисунок 3 – Результат R/S-анализа
Исходя из полученного значения показателя Хёрста, можно сделать вывод о персистентности ряда. Хотя уровень персистентности ряда низок (значение показателя ближе к 0.5, чем к 1, тем не менее лог-приросты курса доллара поддаются моделированию. Они обладают долговременной памятью и выводятся и прогнозируются из своих предыдущих значений. Это оказалось вполне естественным, поскольку персистентные временные ряды очень распространены в природе.
Построение фрактальной модели ARFIMA
Вычисление показателя Хёрста требовалось для определения параметра оператора дробного дифференцирования в модели ARFIMA. Дробно-интегрированные авторегрессионные модели скользящего среднего являются фрактальными и поэтому очень подходят для моделирования курса доллара. Параметр d для такой модели будет равен H-0,5 = 0,1294. Для построения такой модели сначала необходимо дробно дифференцировать исходный ряд курсов доллара по степени d. Далее моделирование будет происходить уже относительно этих разностей.
Для начала необходимо написать разложение разностного оператора 1+L0,1294 в ряд Тейлора. Данная разность будет учитывать значения в несколькие предыдущие периоды. Перед использованием коэффициентов ряда Тейлора необходимо доказать, что при степени d числовая последовательность коэффициентов при лаговых операторах сходится. Для этого воспользуемся признаком Лейбница: 1) докажем, что a1>a2>a3>…>an; 2) докажем, что an стремится к 0.
Доказательство:
1. limk>?-1k+1•j=0kd-j•k!-1k•j=0k-1d-j•k+1!=k-dk=1-dk. При всех конечных значениях k отношение (k+1)-го и k-го членов ряда <1, что означает, что каждый последующий коэффициент меньше предыдущего.
2. Далее нужно сравнить его с рядом 1k, который превосходит его по значению, и при этом стремится к 0. Таким образом, можно сделать вывод, что числовая последовательность коэффициентов при ряде Тейлора также стремится к 0 по признаку Лейбница. Несмотря на то что курс доллара обладает бесконечной долговременной памятью, на мой взгляд, наиболее логичным и оптимальным решением будет ограничить количество членов ряда Тейлора для вычисления разностей, поскольку было бы неправильно оценивать завтрашний курс с учётом курса десятилетней давности.
Таким образом, решено ограничиться 30 предыдущими днями для вычисления каждой из разностей (месяц). В Таблица приведены результаты вычислений значений коэффициентов для каждого лага
Таблица 2 - Коэффициенты при лагах для фрактальных разностей
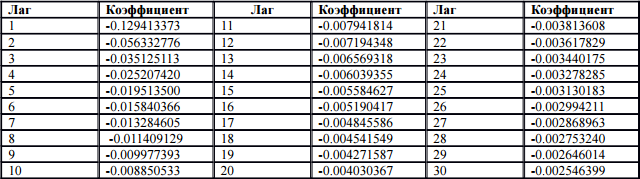
На Рис.4 приведены результаты вычисления разностей на всём исследуемом периоде.
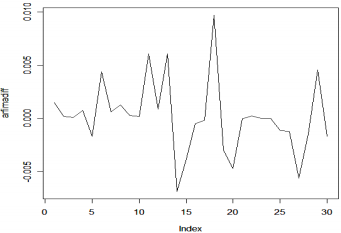
Рисунок 4 – Фрактальные разности для лог-приростов курса доллара
Этот график почти не отличается от исходного по курсам доллара, однако модель этих разностей будет гораздо точнее, чем простая или целая интегрированная модель дневного курса доллара. Для моделирования предпочтительно взять последние 40 значений разностей, поскольку это не слишком превышает месячную динамику и в то же время делает модель значимой. Путём длительного перебора нескольких вариаций был установлен оптимальный вид авторегрессионной модели скользящего среднего (ARMA) для разностей. Ею оказалась модель ARMA(4,7). В Таблица представлены основные характеристики модели.
Таблица 3 - Статистика модели разностей ARMA(4,7)
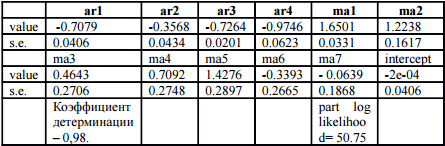
Коэффициент детерминации говорит о том, что модель в целом, несмотря на некоторую пилообразность, хорошо объясняет динамику фрактальных разностей во времени. На Рис. 5 изображён график, показывающий модельный, исходный и прогнозный ряды
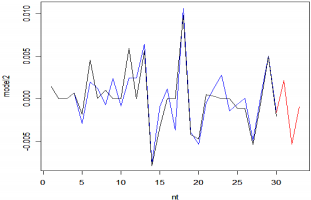
Рисунок 5 – График лог-приростов курса доллара
После моделирования и прогнозирования разностей наступает этап, когда требуется восстановить исходный ряд, имея в распоряжении значения разностей.
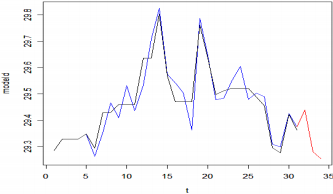
Рисунок 5 – График курсов доллара (модельный вариант)
Построенная модель обладает способностью делать краткосрочные прогнозы курса доллара.
Выводы
После проведённого анализа и моделирования хочется заметить высокие перспективы применения фрактального анализа в изучении свойств финансовых рынков, поскольку, несмотря на то, что данные модели являются высокоточными и эффективными, они не являются вершиной достижений фрактального анализа. В данный момент существуют мультифрактальные модели, применяемые не только для имитации и прогнозирования финансовых рынков, но и в таких сферах, как предсказание землетрясений. Такие модели очень распространены в научных лабораториях Европы, поскольку смысл подобных моделей предполагает проникновение в саму суть и структуру того показателя, который подвергается изучению.
Список использованной литературы
1. Кроновер Р. М. Фракталы и хаос в динамических системах. Основы теории. М.: Постмаркет, 2000. 353с.
2) Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело, 2007. 504 с.
3) Мандельброт Бенуа, Ричард Л. Хадсон (Не)послушные рынки: фрактальная революция в финансах The
Misbehavior of Markets. М.: Вильямс, 2006. 400с.
4) Морозов А.Д. Введение в теорию фракталов. М.; Ижевск: Ин. компьютерных иссл., 2002. 160с.
5) Петерс Э. Фрактальный анализ финансовых рынков: применение теории хаоса в инвестициях и
экономике. М.: Интернет-трейдинг, 2004. 304с.
6) http://ru.wikipedia.org
7) http://www.nsu.ru/phpBB/viewtopic.php?t=19201
8) http://www.cbr.ru/
9) http://fraktals.ucoz.ru/publ/12-1-0-54