МЕТОДИ ПРОГНОЗУВАННЯ ФІНАНСОВИХ РИНКІВ НА ОСНОВІ МУЛЬТИПЛІКАТИВНОЇ МОДЕЛІ

Автори: Мірошниченко О. А., Андрюхін О. І.
Джерело:Мониторинг и экономическая кибернетика – 2012 / Материалы III международной научно-технической конференции студентов, аспирантов и молодых ученых «Информационные управляющие системы и компьютерный мониторинг – 2012» – Донецк, ДонНТУ – 2012.

Анотація

Мірошниченко О. А., Андрюхін О. І. Методи прогнозування фінансових ринків на основі мультиплікативної моделі Розглянуто методи прогнозування фінансових ринків на основі мультиплікативної моделі. В якості залежності досліджуваного ряду використовувалась класична регресійна модель, що враховує дві основні компоненти часового ряду – тренд і циклічна компонента.

Загальна постановка проблеми

Поряд з великими національними фондовими, ф'ючерсними, валютними ринками з'явилися ринки світового масштабу, типовим представником є сучасний фінансовий ринок FOREX.

FOREX являє собою глобальну мережу банків, інвестиційних фондів і брокерських будинків, що включає в себе комп'ютерні інфраструктури, що обслуговують клієнтів, які торгують валютами і для отримання прибутку від зміни валютних курсів здійснюють спекулятивні операції. Денний оборот на ринку FOREX перевищує один трильйон доларів, за прогнозами експертів буде рости і далі.

Відомо, що близько 99% всіх угод на фінансових ринках – спекулятивні, тобто укладаються виключно з метою отримання прибутку за схемою «купити дешевше – продати дорожче». Всі вони засновані на прогнозах змін котирувань учасниками ринку. Для ефективного аналізу ринку потрібні відповідні сучасним вимогам економіко–математичні методи. Сьогодні величезна кількість науковців працюють в галузі розробки методів прогнозування фінансових ринків. Таким чином, дослідження в області біржових ринків – актуальний і перспективний напрямок діяльності і буде залишатися таким протягом досить довгого періоду часу.

Прогнозування &ndash– це передбачення майбутніх подій. Метою прогнозування є зменшення ризику при прийнятті рішень. Прогноз зазвичай виходить помилковим, але помилка залежить від використовуваної прогнозуючої системи. Надаючи прогнозу більше ресурсів, можна збільшити точність прогнозу і зменшити збитки, пов'язані з невизначеністю при прийнятті рішень.

Прогнозування фінансово-економічних часових рядів є надзвичайно актуальною задачею. Сучасні підходи до даної задачі можна охарактеризувати наступними напрямками: 1) апроксимація часового ряду аналітичною функцією та екстраполяція знайденої функції у напрямку майбутнього – так звані трендові моделі [1]; 2) дослідження впливу усіх можливих факторів на показник, який прогнозується та побудова економетричних, або більш складних моделей за допомогою методу групового урахування аргументів (МГУА) [2]; 3) моделювання майбутніх цін як результатів прийняття рішень за допомогою нейронних мереж, генетичних алгоритмів, нечітких множин [3]. На жаль, дані методики не демонструють стабільних прогнозів, що може бути пояснене складністю систем, динаміка яких прогнозується, постійною зміною їх структури [4].

Досліджуваний динамічний ряд є результатом певного процесу. Найбільш поширеним методом вивчення циклічних процесів є класична сезонна декомпозиція. Вона базується на можливості представлення даних часового ряду у вигляді двох моделей – адитивної і мультиплікативної. У цих моделях виділяються три компоненти:

1) Тренд відображає довгострокові зміни, які спостерігаються в часовому ряду, коли циклічна і нерегулярна компоненти вилучені. Передбачається, що тренд можна представити у вигляді прямої лінії.

2) Циклічність відображає коливання в тимчасовому ряді, викликані певними факторами. Циклічний фактор, як правило, повторюється через певний період, хоча точна картина показників ряду може змінюватися.

3) Випадкова компонента – це той вплив, який може спостерігатися після завершення виключення впливу тренду і циклічної факторів.

Щоб описати залежність досліджуваного ряду була запропонована класична регресійна модель, що враховує дві основні компоненти часового ряду – тренд і циклічну компоненту. Вона має вигляд:

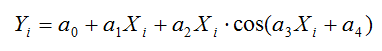
Припускаємо, що якість прогнозу залежатиме від розміру вікна – кількості даних, на основі яких буде побудована залежність, і зміщення цього вікна відносно першого елемента. Прогноз розраховувався на наступну одиницю часу. Якість прогнозу оцінювалося мультиплікативною помилкою.

Розрахунки були проведені в програмному пакеті Maple 15. При розрахунках використовувались наступні показники:

р1 – відношення фактичного значення часового ряду до прогнозованого;

m – розмір вікна часу;

sdv – зміщення часового вікна щодо першого елемента.

В якості досліджуваних даних використовувались значення котирувань ринку FOREX за листопад 2011 року. Аналіз проводився по даним з інтервалом різного проміжку часу (доба, 4 години, 30 хвилин) та зміщення тимчасового вікна щодо першого елемента.

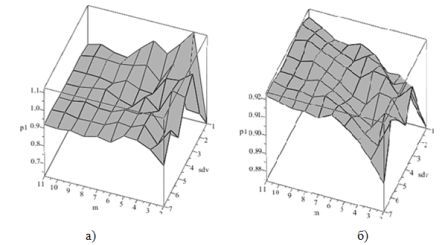
Рис. 1. Залежність якості прогнозу від вікна часу (а – з врахуванням повної залежності параметрів моделі; б – з поетапним виявленням залежності).

Рисунок 1.а зображує залежність якості прогнозу від вікна часу у 10 одиниць при аналізуванні даних ринку FOREX з інтервалом часу 1 день. Під час розрахунку програма враховувала повну залежність і обчислювала відразу всі параметри моделі. Оптимальне відношення значень знаходиться на рівні одиниці. Таким чином, значення р=1,05 у точці m=2 sdv=3 є найбільш оптимальним.

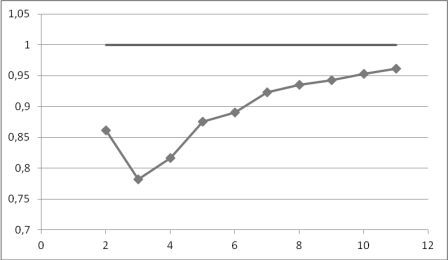
Рис. 2. Залежність якості прогнозу від розміру часового вікна.

На рисунку 2 зображена зміна значення середнього значення відношення фактичного значення часового ряду до прогнозованого за досліджуваний проміжок часу. Таким чином, з збільшенням розміру вікна якість пронозу збільшується. Із розрахунків бачимо, що різниця від найкращої до найгіршої точності прогнозу становить 22,4%.

Аналіз залежності другим методом (рис.1.б) проходив у два етапи: на першому виявлявся тренд, після чого з вихідних даних віднімала значення змодельованого тренда, і по залишку знаходила циклічну залежність.

Оптимальним значенням відношення розміру вікна та зміщення щодо першого елемента є значення р=0,92 у точці m=10, sdv=3.

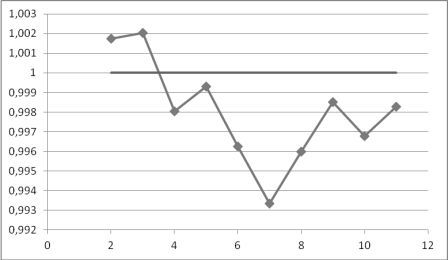
Рис. 3. Залежність якості прогнозу від розміру часового вікна.

Зміна значення середнього значення відношення фактичного значення часового ряду до прогнозованого за досліджуваний проміжок часу при розрахунках другим методом зображено на рисунку 3. Найбільша точність прогнозу спостерігається у часового вікна в 5 пунктів. Різниця найкращої та найгіршої точності прогнозу становить 3,4%, що говорить о більшій надійності даного методу.

На рисунках 4 та 5 зображена залежність якості прогнозу від вікна часу у 20 та 30 одиниць відповідно при аналізуванні даних ринку FOREX з інтервалом часу 4 години.

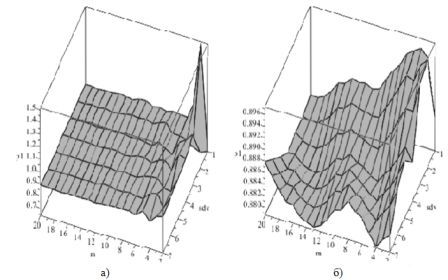
Рис. 4. Залежність якості прогнозу від вікна часу 20 одиниць (а-першим методом; б-другим).

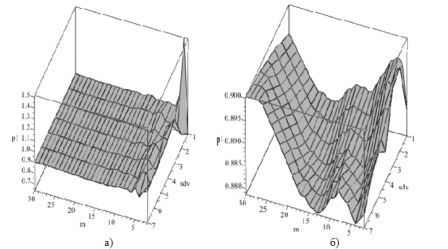
Рис. 5. Залежність якості прогнозу від вікна часу 30 одиниць (а-першим методом; б-другим).

Розрахунки показали, що найбільш оптимальним значенням відношення розміру вікна 20 та зміщення щодо першого елемента (рис.4) першим методом становить р=1,002 у точці m=2, sdv=4, різниця від найкращої до найгіршої точності прогнозу становить 27,1%, другим – у точці m=28, sdv=3, р=0,91, точність прогнозу дорівнює 1,9%.

Висновки.

В даній роботі наведено результаті аналізу значень котирувань ринку FOREX за листопад 2011 року з інтервалом різного проміжку часу та зміщення тимчасового вікна щодо першого елемента. Було визначено, що більша точність прогнозу досягається другим методом із виявленням тренду, але найбільш оптимальні значення досягались з врахуванням повної залежності параметрів моделі першим методом. Отримані результати носять локальний характер для розглянутого часового інтервалу в умовах певної стабільності.

В подальшій роботі будуть застосовуватись технології складних ланцюгів Маркова для прогнозування фінансових часових рядів з порівняльним аналізом отриманих результатів[4,5].

Перелік використаної літератури

1. Принципи моделювання та прогнозування в екології. / Богобоящий В.В., Курбанов К.Р., Палій П.Б., Шмандій В.М.– К.: Центр навчальної літератури, 2004. – 216 с.
2. Зайченко Ю. П. Нечеткие модели и методы в интелектуальных системах: учеб. пособие для иностр. студ. вузов, направления "Компьютерные науки" / Зайченко Ю. П.,М.З. Згуровский. – К.: Слово, 2008. — 344 с.
3. Ежов А.А., Шумский С.А. Нейрокомпьютинг и его применения в экономике и бизнесе. – М., 1998.
4. Чабаненко Д.М. Алгоритм прогнозування фінансових часових рядів на основі складних ланцюгів // Вісник Черкаського університету. – 2010. – Вип 173. – С. 90-102.
5. Prediction of financial time series with hidden markov models/ Yingjian Zhang, Simon Fraser University, 2004.