Система поддержки принятия решений для управления Банкоматами при периодической обработке экстренных заказов
Автор: Ana Karina Miranda, David F. Munoz
Перевод: Google translate и Сандул Юлия Олеговна
Источник: Ana Karina Miranda. DSS to manage ATM cash under periodic review with emergency orders / Ana Karina Miranda, David F. Munoz // Conference: Proceedings of the 37th Winter Simulation Conference, Orlando, FL, USA, December 4-7, 2005. Источник оригинала
Аннотация
Представляется система поддержки принятия решений на основе моделирования (СППР), которая обрабатывает как регулярные (периодические) так и аварийные запросы. Это СППР была разработана, чтобы помочь менеджеру банкомата в выборе соответствующего порядка и времени запросов, а также аварийных запросов. СППР был разработан с использованием программного обеспечения Arena и интегрирует Visual Basic приложение (VBA), которая позволяет пользователю включать фиксированные и переменные затраты заказов, а также обновления спроса и цены поступления.
Введение
В течение нескольких лет, банки установили банкоматы с целью удовлетворения спроса клиентов. Для этого, банкоматы хранить определенное количество наличных денег, которая распространяется в небольших количествах в соответствии с прибывающих клиентов.Соответствующих для управление наличностью запасами, следует искать равностепенной весия между стоимостью услуг и уровня обслуживания, другими словами, большой перечень законопроектов предполагает высокие финансовые затраты, но в то же время соответствующий уровень инвентаризации необходимо для удовлетворения потребительского спроса.
При использовании либо непрерывную или периодическую систему отзыв инвентарь, простые политики инвентаризации могут быть реализованы (см, например, Nahmias 1997). Тем не менее, в данном случае банкоматов, он является общим, чтобы применить комбинацию регулярных заказов по периодический обзор политики и экстренных заказов при непрерывном политики обзора. Эта комбинация особенно привлекательным из-за высоких затрат дефицитных и большой изменчивости спроса. Тем не менее, критерии, используемые для определения потребности в экстренном порядке не определена, то есть, как правило, администратор эмпирически решает, когда денежные средства в банкомате недостаточно, чтобы удовлетворить спрос для остальной части периода и ставит экстренное заказпроизвольное количество.
Некоторые авторы лечить подобные проблемы. Moinzadeh и Nahmias (1988) Рассмотрим случай непрерывного обзора политики для регулярных и экстренных заказов. Примерно оптимальные политика заказ предлагается для расширения стандарта (Q, R) политики, чтобы два разных размеров лота (Q1 и Q2) и два различных уровня повторного заказа (R1 и R2). Moinzadeh и Шмидт (1991), полученный поведение стационарного для (S-1, S) инвентаризации системы с Пуассона спроса и двумя режимами питания: регулярное и чрезвычайное положение, последний использует информацию о возрасте выдающаяся заказов. Чан (2001) разработали динамическую модель программирования для обзора системы периодической, в которой чрезвычайных заказы могут быть размещены в начале каждого периода (также под периодического обзора политики). Автор разработал оптимальную политику заказа, которые минимизируют общее ожидаемое закупок, проведения и затраты нехватки. Эта статья расширяет результаты Чан Кайши и Гутьеррес (1996). Ким и др. (2002) сравнить толкать и тянуть политики (с точки зрения производителя) в присутствии срочных заказов. В этой статье моделирования был использован для проведения экспериментов, считая, что регулярные заказы следовать (S, S) периодический обзор политики, и время между прибытием экстренных заказов соответствует экспоненциальному распределению. Важно отметить, что ни один из вышеперечисленных случаев не рассмотрим конкретную ситуацию регулярных заказов с периодического обзора политики и экстренных заказов с непрерывным политики повторного просмотра с точки зрения продавца. Кроме того, более, как в Ким и др. (2002) и Moinzadeh и Nahmias (1988) моделирование используется в качестве инструмента для проверки результатов.
Эта статья представляет собой систему поддержки принятия решений (DSS), разработанной, чтобы помочь менеджеру в выборе соответствующих регулярных и чрезвычайных порядка размеров, а также точку заказа для данного уровня обслуживания. Как отмечается в следующих разделах, модель, связанная с DSS эффективно включает ограничения процесса, а также количественные и качественные факторы, связанные с управлением наличных денег в банкомате.
Проектирование системы
СППР был разработан в Арене (Келтон др. 2004) и состоит из двух основных элементов;Первый интерфейс, который связывает пользователя с системой.Второй моделью, которая имитирует прибывших клиентов и политики инвентаризации. Рисунок 1 иллюстрирует общую структуру СППР.
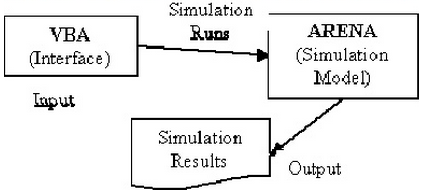
Рисунок 1 – Общая структура СППР
Интерфейс был разработан в VBA с намерением облегчить управление данными и ввод данных для пользователя. С помощью этого интерфейса, пользователь просто вводит информацию, относящуюся к мощности банкомата, первоначальный перечень, регулярные и чрезвычайные расходы, задержки, прогнозы спроса и прогнозы об ожидаемых клиентских прибывших. Рисунок 2 иллюстрирует окно пользовательского интерфейса и 3 иллюстрирует окно, связанный с повседневной данным прогноза, который используется, чтобы ввести ожидаемое количество клиентов и ожидаемого спроса каждого клиента на ежедневной основе в срок.
Имитационная модель состоит из двух суб-моделей, которые работают одновременно, первая соответствует системе периодического обзора и второй относится к аварийной. Параметры, необходимые для обеих моделей, чтобы запустить были введены в интерфейсе, например, регулярные и экстренные расходы на заказ состоят каждый из транспортных и страховых расходов (рисунок 2) и требуется вычислить общую стоимость заказа. Кроме того, минимальные и максимальные задержки раз используются в качестве параметров равномерных распределений (в связи с тем, что она является обычной практикой в Мексике, чтобы случайным образом повторно питания банкомат между минимальным и максимальным временем для предотвращения кражи). Начальные значения для переменных решения (размерами порядка и сортировка пунктов) сначала устанавливается на основе эвристических процедур (для более подробной информации см Miranda, 2004).

Рисунок 2 – Пользовательский интерфейс
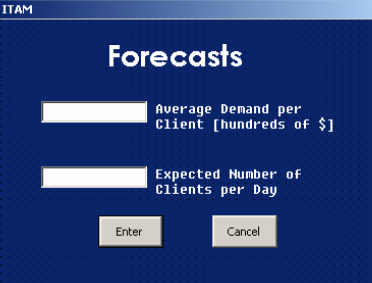
Рисунок 3 – Окно для ежедневного прогноза
Клиентские поступления в любой день моделируются в соответствии с нестационарным Пуассоновским процессом, что, вероятно, наиболее широко используемым инструментом для этой цели (Закон и Келтон 2000). НЗСТ является процесс подсчета {N (t), t> = 0}, где N (t) представляет собой общее число клиентов, которые прибывают в интервале (0, t). НЗСТ позволяет во время выполнения менять темпы поступления, и среднее число прибывших в единицу времени определяется функцией:

где λ(у) функция интенсивности процесса (Росс, 2003).
Имитационная модель предполагает, что функция интенсивности на определенный день определяется по формуле:
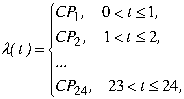
где t выражено в часах, С представляет собой шкалу постоянным, а Р1, Р2, Р3, ..., Р24 определения скорости прибытия в каждый час.
Потому что 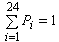 , ожидаемое число прибывших в определенный день:
, ожидаемое число прибывших в определенный день:

Таким образом, значение С в течение определенного дня получается путем умножения ожидаемого числа клиентов в день по средней потребности каждого клиента (рисунок 3), и Pi предполагаются одинаковыми для каждого дня, которые, как ожидается чтобы оценить на основе исторических данных.
Рисунок 4 представляет собой возможный график m(t). На этом графике по величине скорость прибытия соответствует час 3, в то время часов 1 и 24 являются часы с наименьшей интенсивностью
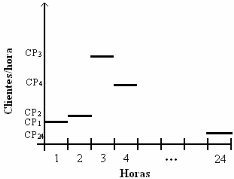
Рисунок 4 – График интенсивности Функции
Для моделирования спроса клиент законопроект, биномиальное распределение (с параметрами М и р в данный день) предполагалось, потому что он обладает двумя желаемыми свойствами: 1) он принимает дискретные значения, и 2) это ограниченные.Первое свойство отражает тот факт, что банкомат обеспечивает целое число законопроектов и второй, что есть максимальное количество законопроектов, которые могут быть предоставлены клиенту в одном отзыве, потому что политик безопасности. Таким образом, параметр М равен максимальному числу счетов, которые могут быть предоставлены и р равно среднему спроса на клиенте в соответствующий день (смотри рисунок 3), деленное на M ..
Стоит отметить, что в то время как в первом варианте исторических данных СППР не используется для регулировки спрос каждого клиента, он может быть включен как мы это делали в процессе прибытия. В этом случае, мультиномиальный распределения возможных значений спроса могут быть предложены, и вероятности могут быть скорректированы на основе исторических данных. Кроме того, можно объединить исторические прогнозы данных и пользователя с помощью байесовского вывода (см Муньоса, 2003), в этом случае в результате моделирования исторических данных с мультиномиальных распределений, адекватной до распределения может быть распределение Дирихле (см О'Хаган и Форстер 2004 ).
Наконец, с помощью Opt Quest для Arena, процедура была реализована в СППР, чтобы получить оптимальный (не менее общей стоимости) значения (s, S) для обзора политики и периодического (г, Q) для политики чрезвычайной обзора, с учетомуровень обслуживания указанный пользователем.Процедура начинается с начальных значений, полученных из эвристического приближения и поисков Opquest для оптимальных значений, которые обеспечивают наименьшее общую стоимость.
Результаты и выводы
С целью выявления переменных, которые влияют на оптимальные значения параметров (размеры порядка и повторного заказа пунктов), серия экспериментов были проведены сначала изменения спроса, а затем задержки (регулярный и аварийный). Различные значения максимального нормального задержки (34, 37, 40, 43 и 46 часов) были протестированы в двух случаях: низкого и высокого спроса.Минимальная задержка нормальная был установлен в 24 часов во всех случаях, потому что короче задержка не возможно в Мехико. Как показано на рисунках 5, 6, 7 и 8, оптимальные значения S, Q и R являются чувствительными к изменениям в условиях максимального нормального задержки, вопреки тому, что можно наблюдать на оптимальных значений S.
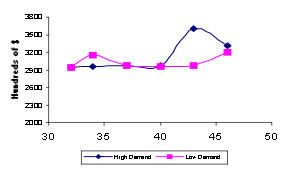
Рисунок 5 – Точка заказа s при различных значениях максимального нормального задержки

Рисунок 6 – Изменение размера S при различных значениях максимальной нормальной задержке
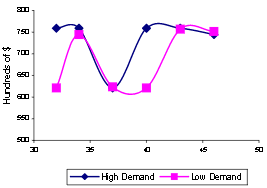
Рисунок 7 – Периодическая точка заказа r при различных значениях максимальной нормальной задержке
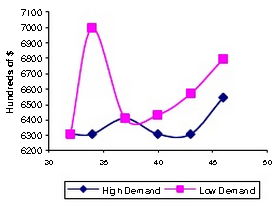
Рисунок 8 – Размер участка Q при различных значениях максимальной нормальной задержке
Наконец, мы запускаем серию экспериментов для различных значений максимальной задержки аварийного (10, 12, 14, 16 и 18 часов) при низкой и высокой спроса. Как видно из рис 9 и 10, оптимальных значений с и S являются Sensi-ный к изменениям в максимальной задержкой аварийного когда спрос низкий, в то время как это не относится к высоким спросом.
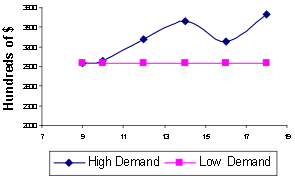
Рисунок 9 – Точка заказа s при различных значениях задержки Максимальная скорой
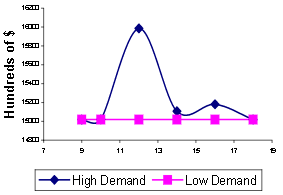
Рисунок 10 – Изменение размера S при различных значениях задержки Максимальная скорой
Как упоминалось ранее, разработанная СППР может быть весьма полезна, поскольку она позволяет включение источников неопределенности, таких как: прибывших клиентов, спроса, и времени задержки. Применение этого СППР может также обеспечить экономические выгоды, результат предлагает оптимальные размеры заказов и оптимальные регулярные и экстренные повторения заказа.
Список использованной литературы
1. Kelton, W. D., Sadowski, R. P., and Sturrock, D. T., 2004, Simulation with Arena, 3rd Ed., Mc.Graw Hill, New York.
2. Law, A., and Kelton, W. D., 2000, Simulation Modeling and Analysis. Mc. Graw Hill, NewYork.
3. Miranda, A. K., 2004, Desarrollo de un Sistema para Administrar Inventarios con RevisionPeriodica y Revision de Emergencia, Industrial Engineering Degree Dissertation, EngineeringDivision, Instituto Tecnologico Autonomo de Mexico, Mexico City.
4. Munoz, D. F., 2003, A Bayesian Framework for Modeling Demand in Supply Chain SimulationExperiments, Proceedings of the 2003 Winter Simulation Conference, S. Chick, P. J. Sanchez,D. Ferrin y D. J. Morrice (eds.) 1319-1325, Institute of Electrical and Electronics Engineers Inc.,New Orleans.
5. Nahmias, S., 1997, Production and Operations Analysis, 3rd Ed., Mc. Graw Hill, New York.
6. O’Hagan, A., and Forster, J., 2004, Kendall?s Advanced Theory of Statistics Volume 2BBayesian Inference, 2nd Ed., Oxford University Press Inc., New York.
7. Ross, S., 2003, Introduction to Probability Models. Academic Press, San Diego.