Аннотация
Казанцев А.В Элементы аналитической геметрии Рассмотрены способы математического описания объектов в трехмерном пространстве или на плоскости.
Элементы аналитической геометрии
Для того чтобы уметь синтезировать изображения на экране компьютера необходимо предложить способ математического описания объектов в трехмерном пространстве или на плоскости. Окружающий нас мир с точки зрения практических приложений описывают как трехмерное евклидово пространство. Под описанием трехмерного объекта будем понимать знание о положении каждой точки объекта в пространстве в любой момент времени. Положение точек в пространстве удобно описывается с помощью декартовой системы координат.
Для того чтобы ввести декартову систему координат проведем три направленные прямые линии, не лежащие в одной плоскости, которые называются осями, в трехмерном пространстве так чтобы они пересекались в одной точке – начале координат. Выберем на этих осях единицу измерения.
Тогда положение любой точки в пространстве будем описывать через координаты этой точки, которые представляют собой расстояния от начала координат до проекций точки на соответствующие оси координат. Проекцией точки на координатную ось называется точка пересечения плоскости, проходящей через заданную точку и параллельной плоскости, образованной двумя другими осями координат. Например, на рис. 1 проекцией точки P на ось Ox является точка Q, которая принадлежит плоскости, параллельной плоскости zOy .
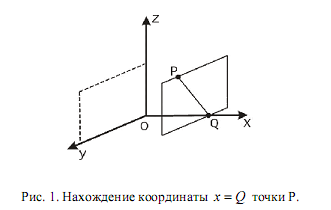
В общем случае оси системы координат могут располагаться под произвольными, хотя и фиксированными углами друг относительно друга.
Для практических расчетов гораздо удобнее когда эти оси расположены взаимно перпендикулярно. Такая система координат называется ортогональной. В ортогональной системе координат проекцией точки P на ось является единственная точка на оси такая, что отрезок прямой, проведенной из этой точки к точке P является перпендикулярным к данной оси.
Таким образом, положение в пространстве точки P описывается ее координатами, что записывается как P=(x,y,z) . Взаимное расположение осей в ортогональной системе координат в трехмерном пространстве может быть двух видов. Проведем ось Ox слева направо, а ось Oy снизу вверх, как показано на рис. 2.
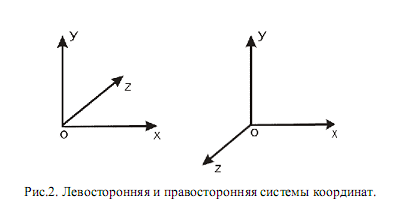
Ось Oz при этом может проходить как в направлении от наблюдателя в плоскость листа, так и от плоскости листа к наблюдателю. В первом случае система координат будет называться левой или левосторонней, а во втором случае – правой или правосторонней. Более точное определение правой и левой систем координат можно дать следующее.
Если посмотреть из положительной полуоси Oz в направлении начала координат, то для совмещения положительной полуоси Ox с положительной полуосью Oy необходимо повернуть Ox относительно начала координат против часовой стрелки – в этом случае имеем правую систему координат; если же поворот производится по часовой стрелке – то система координат левая.
Существует также легкий способ определения вида системы координат по правой или левой руке, как показано на рис. 3. Для левой руки большой, указательный и средний пальцы формируют левую тройку ортогональных векторов. То же относится и к их циклическим перестановкам.
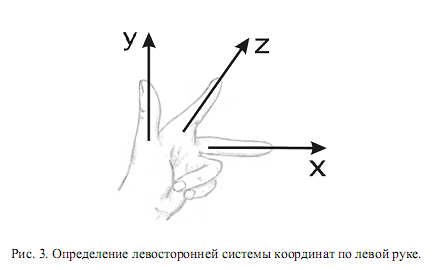
Декартовы координаты точек позволяют описывать статичное положение объектов в пространстве. Однако для проведения каких-либо действий над объектами необходимо иметь дополнительные математические конструкции. В качестве одной из таких конструкций применяют радиус-векторы. Радиус-векторы обладают всеми свойствами векторов, но имеют одну особенность: начало радиус-вектора находится всегда в начале координат, а конец радиус-вектора лежит в некоторой точке пространства.
Это свойство радиус-векторов позволяет поставить во взаимно однозначное соответствие всем точкам пространства соответствующие им радиус-векторы.
Формально это соответствие запишем в следующем виде. Пусть точка P имеет координаты (x,y,z) , то есть P(x,y,z), и p=xi+yj+zk – радиус-вектор, конец которого находится в точке P , где k j, i, – тройка единичных базисных векторов, или просто нормированный базис. Тогда точке P взаимно однозначно соответствует радиус-вектор p , или P(x,y,z)<->xi+yj+zk=p . Таким образом, можно легко переходить от координат точек к радиус-векторам и обратно. Далее мы увидим что представление радиус-вектора в виде линейной комбинации векторов базиса имеет вполне конкретное практическое применение. Отметим, что радиус-вектор иногда определяют как преобразование переноса точки из начала координат в заданную точку пространства с известными координатами.
Список использованной литературы
1. Ньюмен, Спрулл, Основы интерактивной машинной графики, М. Мир,
1976.
2. Энджел Й. Практическое введение в машинную графику, Радио и Связь,
1984.
3. А. Вэн-Дэм, Дж. Фоли, Основы интерактивной машинной графики, т.1-2,
М. Мир, 1985.
4. Е.В. Жикин, А.В.Боресков, Компьютерная графика. Динамика,
реалистические ихображения, М., Диалог-МИФИ, 1995, 1997.
5. Л. Аммерал, Машинная графика на языке С, в 4-х томах, изд-во Сол.
Систем, 1992.
6. Компьютер обретает разум. Пер. с англ. Под ред. В.Л.Стефанюка, М. Мир,
1990.
7. Роджерс, алгоритмические основы машинной графики. М. Мир, 1989.