Реферат по теме выпускной работы
Содержание
- Введение
- 1 Актуальность темы
- 2 Цель и задачи исследования, планируемые результаты
- 3 Основные понятия и свойства контуров
- 3.1 Понятие контур
- 3.2 Свойства контуров
- 3.3 Скалярное произведение контуров
- 3.4 Корреляционные функции контуров
- 3.5 Автокорреляционная функция
- 3.6 Общий алгоритм распознавания
- 3.7 Оценка продуктивности алгоритмов в контурном анализе
- 3.8 Дескриптор контура
- 3.9 Сверстка автокорреляционной функции
- 3.10 Эквализация контуров
- Выводы
- Список источников
Введение
С развитием вычислительной техники стало возможным решать задачи, которые ранее считались невыполнимыми на персональных компьютерах. Создание устройств, выполняющих функции распознавания объектов в видеопотоке, в большинстве случаев позволит заменить человека – специализированным автоматом. Стоит заметить, что качество выполнения работы человеком зависит от многих факторов (квалификация, опыт, усталость, интерес). В то же время исправная и настроенная система будет работать, обеспечивая всегда одинаковое качество выполнения работы. Еще одним плюсом замещения человека машиной – несравнимое преимущество автоматических систем в быстродействии.
На сегодняшний день в каждом городе, мегаполисе существует транспортные пробки, которые в пиковые часы достигают сотен километров, наземный общественный транспорт значительно снижает свою провозную возможность и становится малопривлекательным для пассажиров, затрудняется передвижение экстренного и служебного транспорта, возрастает количество мелких аварий, нарушений ПДД, от стоящих и работающих на самом «вредном» холостом ходу автомобилей увеличивается загазованность воздуха и т. п.
Основная причина транспортной проблемы заключается в изначальной планировке города без учета возможностей широкого использования личных автомобилей. Планировка улиц, например, в Москве радиально-кольцевая и теоретически имеет важное преимущество перед прямоугольной (как, например, в Нью-Йорке), поскольку за счет диагональных маршрутов она минимизирует время перемещения по городу. Но на практике такая конфигурация дорог приводит к тому, что центр города, соединяющий радиальные магистрали, часто превращается в одну сплошную пробку.
Ручная регулировка или применения светофоров проблему организации эффективного передвижения в большом городе не решают. Поэтому автоматизированный контроль за движением автомобильного транспорта - это задача необходима и актуальна, а одним из современных методов распознавания проблемных ситуаций по применению компьютерной техники является контурный анализ.
1 Актуальность темы
Методы контурного анализа в современности достаточно широко применяются в радиотехнических системах, в системах связи, для ориентации летательных аппаратов [1], в процессе контроля за передвижением автомобилей, для детектирования номеров машин, контроля скорости или нарушений правил дорожного движения [2]. Контур - это наиболее информативный структурный элемент объекта. Однако качественное выделение контура - это одна из самых сложных проблем обработки визуальной информации. Известны методы решения задач контурного анализа с помощью библиотеки OpenCV, но этот пакет предназначено для решения задачи подсчета объектов, имеющих визуально заметную точку на изображении. А контуры часто имеют такие недостатки, как разрывы, наличие лишних линий, которые не соответствуют изучаемому объекту.
Поэтому создание и внедрение программного обеспечения для контроля автомобильного транспорта позволит контролировать пропускную способность дорог и решить проблему образования транспортных пробок.
2 Цель и задачи исследования, планируемые результаты
Цель данной работы – разработка контурного алгоритма для программного обеспечения системы контроля автомобильного трафика.
Объект разработки – программное обеспечение, обеспечивающее контроль автомобильного трафика путем контурного анализа изображений состояния проезжей части дороги, получено с камер наблюдения.
Предмет разработки – современные средства проектирования и разработки программного обеспечения: MS Visio 2013, язык С#, среда разработки MS Visual Studio 2012. Для достижения поставленной цели необходимо решить следующие задачи:
1) провести обзор существующих систем;
2) рассмотреть основные принципы построения алгоритмов контурного анализа, проанализировать оценку их производительности;
3) выбор оптимального алгоритма для реализации системы;
4) обоснование языка программирования и среды разработки;
5) спроектировать архитектуру системы;
6) разработать программное обеспечение системы.
3 Основные понятия и свойства контуров
3.1 Понятие контур
Контурный анализ позволяет описывать, хранить, сравнивать и производить поиск объектов, представленных в виде своих внешних очертаний – контуров. Контур – это граница объекта, совокупность точек (пикселов), отделяющих объект от фона [3]. Предполагается, что контур содержит всю необходимую информацию о форме объекта. Внутренние точки объекта во внимание не принимаются. Это ограничивает область применимости алгоритмов контурного анализа, но рассмотрение только контуров позволяет перейти от двумерного пространства изображения – к пространству контуров, и тем самым снизить вычислительную и алгоритмическую сложность. Контурный анализ позволяет эффективно решать основные проблемы распознавания образов – перенос, поворот и изменение масштаба изображения объекта.
В системах компьютерного зрения используется несколько способов кодирования контура – наиболее известны код Фримена, двумерное кодирование, полигональное кодирование. Но все эти способы кодирования не используются в контурном анализе. Вместо этого, в контурном анализе контур кодируется последовательностью, состоящей из комплексных чисел. На контуре фиксируется точка, которая называется начальной точкой. Затем, контур обходится (допустим – по часовой стрелке, см. рис.1. – «Кодирование контура»), и каждый вектор смещения записывается комплексным числом a+ib. Где a – смещение точки по оси X, а b – смещение по оси Y. Смещение берется относительно предыдущей точки.
Каждый вектор контура будем называть элементарным вектором (ЭВ). А саму последовательность комплекснозначных чисел – вектор-контуром (ВК). Вектор–контуры будем обозначать большими греческими буквами, а их элементарные вектора – малыми греческими буквами.Таким образом, вектор-контур Г длины k можно обозначить как:
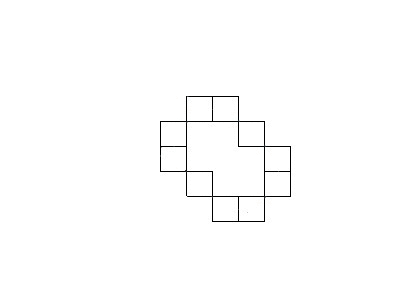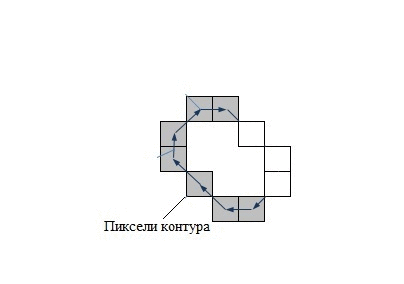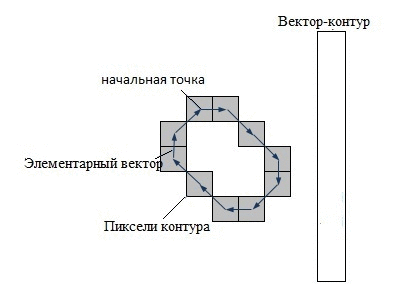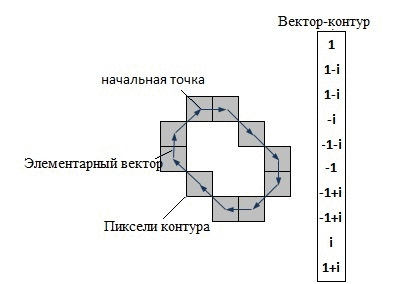
Рисунок 1 – Кодирование контура (анимация: 7 кадров, 15 циклов повторения, 74 килобайта)
Комплексное кодирование близко к двумерному кодированию, где контур определяется как совокупность ЭВ, представленных своими двумерными координатами. Но разница в том, что операция скалярного произведения для векторов и для комплексных чисел – различны. Именно это обстоятельство и дает преимущество методам контурного анализа.
3.2 Свойства контуров
Рассмотрим свойства контуров:
1. Сумма элементарных векторов замкнутого контура равна нулю. Это тривиально – поскольку элементарные векторы приводят в начальную точку, значит их сумма равна нуль-вектору.
2. Контур-вектор не зависит от параллельного переноса исходного изображения. Поскольку контур кодируется относительно начальной точки, то этот способ кодирования инвариантен сдвигу исходного контура.
3. Поворот изображения на определенный угол равносилен повороту каждого ЭВ контура на тот же угол.
4. Изменение начальной точки ведет к циклическому сдвигу вектору контура. Поскольку элементарным вектором кодируются относительно предыдущей точки, то понятно, что при изменении начальной точки последовательность элементарного вектора будет та же самая, но первым элементарным вектором будет тот, который начинается в начальной точке.
5. Изменение масштаба исходного изображения можно рассматривать как умножение каждого элементарного вектора контура на масштабный коэффициент.
3.3 Скалярное произведение контуров
Скалярным произведением контуров Г и N называется такое комплексное число:
η = (Г, N) = ∑(k-1) n=0(Yn,Vn)
где k – размерность вектор-контура;
Yn — n-й элементарный вектор контура Г;
Vn — n-й элементарный вектор контура N;
(Yn, Vn) — скалярное произведение комплексных чисел, вычисляемое как:
(a + ib, c + id) = (a + ib) (c – id) = ac + bd + i (bc – ad)
В контурном анализе допускается скалярное произведение только ВК одинаковой размерности. То есть число элементарных векторов в контурах должно совпадать [4].
Скалярное произведение обычных векторов и скалярное произведение комплексных чисел – отличаются. Если бы мы перемножали ЭВ как простые вектора, то их скалярное произведение выглядело бы так:
((a, b), (c, d)) = ac + bd
При сравнении (2.3) и (2.2) можно заметить следующее.
1. Результатом скалярного произведения векторов является действительное число. А результатом произведения комплексных чисел является комплексное число.
2. Действительная часть скалярного произведения комплексных чисел совпадает со скалярным произведением соответствующих векторов. То есть комплексное произведение включает в себя векторное скалярное произведение.
В линейной алгебре скалярное произведение равно произведению длин векторов на косинус угла между ними. Это значит, что два перпендикулярных вектора всегда будут иметь нулевое скалярное произведение, коллинеарные же вектора – напротив, будут давать максимальное значение скалярного произведения.
Эти свойства произведения позволяют использовать его как определенную меру близости векторов. Чем оно больше – тем меньше угол между векторами, тем «ближе» они друг к другу. Для перпендикулярных векторов – оно опускается до нуля, и далее становится отрицательным для векторов, направленных в разные стороны. Скалярное произведение (2.1) также обладает похожими свойствами. Введем еще одно понятие – нормированное скалярное произведение (НСП):
η = (Г, N)/|Г||N|
где |Г| и |N| — нормы(длины) контуров, вычисляемые как:
Г = (∑(k-1) n=0 |Yn 2)21/2
НСП в пространстве комплексных чисел, также является комплексным числом. При этом, единица – это максимально возможное значение модуля НСП (это следует из неравенства Коши-Буняковского: |ab|*|a||b|), и она достигается только если:
Г = µN
где µ – произвольное комплексное число.
При умножении комплексных чисел, их модули (длины) перемножаются, а аргументы (углы) – складываются. Значит контур N это тот же контур N, но повернутый и промасштабированный. Масштаб и поворот определяется комплексным числом. Итак, модуль НСП достигает максимального значение – единицы, только если контур Г является тем же контуром N, но повернутым на некоторый угол и про масштабированный на определенный коэффициент [5].
3.4 Корреляционные функции контуров
НСП является чрезвычайно полезной формулой для поиска похожих между собой контуров. К сожалению, есть одно обстоятельство не позволяющее использовать его напрямую. И это обстоятельство – выбор начальной точки. Равенство (2.6) достигается только если начальные точки контуров – совпадают. Если же контуры одинаковы, но отсчет ЭВ начинается с другой начальной точки, то модуль НСП таких контуров не будет равен единице. Введем понятие взаимокорреляционной функции (ВКФ) двух контуров:
(m) = (Г,N(m)), m = 0,…, k – 1
Для примера, если N=(n1, n2, n3, n4), то N(1)=(n2, n3, n4, n1), N(2)=(n3, n4, n1, n2) и так далее. Значения этой функции показывают насколько похожи контуры Г и N, если сдвинуть начальную точку N на m позиций. ВКФ определена на всем множестве целых чисел, но поскольку циклический сдвиг на k приводит нас к исходному контуру, то ВКФ является периодической, с периодом k. Поэтому нас будет интересовать значения этой функции только в пределах от 0 до k-1. Найдем величину, имеющую максимальный модуль среди значений ВКФ:
Ψmax = max(Ψ(m)/|Г||N|). m = 0, ....., k - 1
3.5 Автокорреляционная функция
Из определений НСП и ВКФ, понятно, что ?max является мерой похожести двух контуров, инвариантной переносу, масштабированию, вращению и сдвигу начальной точки. При этом, модуль |max| показывает степень похожести контуров, и достигает единицы для одинаковых контуров, а аргумент arg (max) дает угол поворота одного контура, относительно другого.
Введем еще одно понятие – автокорреляционной функции (АКФ). Автокорреляционная функция является ВКФ для которой N=Г. По сути – это скалярное произведение контура самого на себя при различных сдвигах начальной точки:
v (m) = ( Г, Г(m) ), m = 0, … , k – 1
Рассмотрим некоторые свойства АКФ.
1. АКФ не зависит от выбора начальной точки контура. Действительно, посмотрим на определение скалярного произведения (1). Как видим, изменение начальной точки приведет просто к изменению порядка суммируемых элементов и не приведет изменению суммы. Этот вывод не столь очевиден, но если вдуматься в смысл АКФ, то он ясен.
2. Модуль АКФ симметричен относительно центрального отсчета k/2. Поскольку АКФ является суммой попарных произведений ЭВ контура, то каждая пара встретится два раза на интервале от 0 до k. Пусть, например, N=(n1, n2, n3, n4), распишем значения АКФ для разных m:
АКФ(0)=(n1,n1)+(n2,n2)+(n3,n3)+(n4,n4)
АКФ(1)=(n1,n2)+(n2,n3)+(n3,n4)+(n4,n1)
АКФ(2)=(n1,n3)+(n2,n4)+(n3,n1)+(n4,n2)
АКФ(3)=(n1,n4)+(n2,n1)+(n3,n2)+(n4,n3)
АКФ(4)=(n1,n1)+(n2,n2)+(n3,n3)+(n4,n4)
Дополнения в АКФ(1) те же самые, что и в АКФ(3), с точностью до перестановки множителей. Для комплексных чисел (a, b) = (b, a)*, получаем что АКФ(1)=АКФ(3)*, где * — знак сопряженного комплексного числа. А поскольку |a*|=|a|, то получается что модули АКФ(1) и АКФ(3) – совпадают. Аналогично, совпадают модули АКФ(0) и АКФ(4). Далее мы везде будем под АКФ понимать только часть функции на интервале от 0 до k/2, поскольку остальная часть функции – симметрична первой части. Если контур имеет какую-либо симметрию относительно поворота, то аналогичную симметрию имеет его АКФ.
Для примера, приведем графики АКФ для некоторых контуров. На рисунке 2 модуль АКФ изображен синим цветом (АКФ изображена только для интервала от 0 до k/2). Все контуры, кроме последнего имеют симметрию к повороту, что приводит к симметрии АКФ. Последний же контур такой симметрии не имеет, и график его АКФ – не симметричен.
АКФ контура можно считать характеристикой формы контура. Так, формы, близкие к кругу имеют равномерные значения модуля АКФ (см рисунок для круга). Сильно вытянутые в одном направлении формы – имеют провал в центральной части АКФ (см рисунок прямоугольника). Формы, переходящие в самих себя при повороте, имеют максимум АКФ в соответствующем месте (см. рис. 2 для квадрата) [6-9].
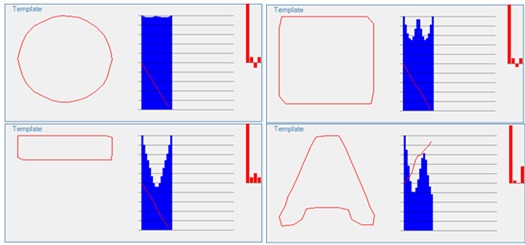
Рисунок 2 – Графики контуров для некоторых контуров
Нормированная АКФ не зависит от масштаба, положения, вращения и выбора начальной точки контура. Это следует из пункта 1-го и из свойств НСП.
3.6 Общий алгоритм распознавания
Общая последовательность действия при распознавании выглядит так:
1) предварительная обработка изображения — сглаживание, фильтрация помех, повышение контраста;
2) бинаризация изображения и выделение контуров объектов;
3) начальная фильтрация контуров по периметру, площади, коэффициенту формы, фрактальности и так далее;
4) приведение контуров к единой длине, сглаживание;
5) перебор всех найденных контуров, поиск шаблона, максимально похожего на данный контур.
3.7 Оценка продуктивности алгоритмов в контурном анализе
Сделаем оценку быстродействия алгоритмов, основанных на контурном анализе. Пусть изображение уже бинаризировано и на нем выделены контуры. Поскольку в дальнейшем мы будем работать только с точками контуров, оценим общее их количество на изображении. Возьмем изображение размером n*n пикселов. Покроем его равномерной сеткой с шагом s. Суммарная длина всех линий сетки составит:
L = 2n2 /s
Переход от плоского двумерного изображения к контурам не уменьшает размерность задачи.
Замечания.
1. Приведенная оценка является экстремальной. В реальном изображении далеко не все контуры имеют минимальный размер, и они не покрывают всю площадь изображения. Следовательно, число контуров и их суммарный периметр может быть значительно меньше 2n2/s. В идеальном случае – если изображение содержит один объект, без помех, то КА будет работать только с одним контуром, и число его пикселов составит уже не квадратичную, а линейную зависимость от n. В случае же работы с изображением, как с двумерным массивом пикселов (например, применяя каскадные фильтры Хаара) — мы всегда работаем со всеми пикселами изображения, независимо от того, сколько объектов на нем изображено. Поскольку изображение в виде контуров уже имеет естественную сегментацию — разбито на контуры, то можно осуществлять фильтрацию частей изображения по простым признакам. Среди них – площадь контура, периметр, отношение квадрата периметра к площади (коэффициент формы). Таким образом, есть достаточно простой и эффективный механизм предварительной фильтрации частей изображения.
2. Базовые алгоритмы двумерных методов, как правило, не инвариантны к масштабу (SURF, SIFT) или вращению(Хаар). Поэтому, фактически, они работают в трехмерном пространстве, где еще одно измерение появляется из-за необходимости перебирать масштабы или углы поворота. Поскольку методы КА инвариантны к масштабу и вращению, то здесь такой проблемы не существует (исключение – не инвариантность к начальной точке, но ниже мы рассмотрим эффективные методы борьбы с этой сложностью).
3. Контурный анализ позволяет обрабатывать изображение в прогрессивном режиме. Это значит, что мы можем отсортировать контуры по каком-либо признаку (например, по площади или по градиенту границ, или по яркости и т.п.). А затем обработать первый контур, и выдать результат. Остальные же контуры обрабатывать в фоновом режиме. Это значит, что первый результат (а во многих прикладных задачах именно он и нужен) может быть получен за O(n), что является отличной оценкой для алгоритмов распознавания изображений.
4. Поскольку контуры независимы друг от друга, то алгоритмы распознавания легко распараллеливаются. Кроме того, алгоритмы очень просты и могут выполняться на графических процессорах.
5. Все вышеприведенные размышления касаются только обработки контуров. Разумеется, этап получения самих контуров никуда не исчезает, и он требует как минимум O(n2) [10-12]. Сам контур, по сути, является одномерным объектом. Это вектор комплекснозначных чисел. Однако число контуров возрастает пропорционально квадрату размера изображения. Самым эффективным средством увеличения производительности является уменьшение числа контуров предварительной фильтрацией. Оценим сложность обработки отдельно взятого контура. Скалярное умножение требует O (k) операций, где k - длина контура. Для вычисления ВКФ нужно провести k вычислений скалярных произведений. ПКФ требует вычислений порядка O (k2). Учитывая, что сравнение идет не с одним шаблоном, а с множеством шаблонов, то полное время поиска шаблона для контура можно оценить как:
O (k2t)
где k – длина контура,
t – число шаблонных контуров.
3.8 Дескриптор контура
Не смотря на то, что k – константа (процесс приведения контуров к единой длине мы рассмотрим далее), все равно, вычисление ВКФ — трудоемкий процесс. При k=30 на вычисление ВКФ требуется 900 операций умножения комплексных чисел. А при наличии t=1000 шаблонов, поиск шаблона для контура требует около миллиона умножений комплексных чисел.
Сам процесс скалярного умножения можно ускорить, путем стандартизации контура и введения табличного умножения. Но это не решает проблему кардинально. Кроме того, затраты на стандартизацию – тоже велики, и могут перекрыть достоинства данного подхода. Поэтому мы введем более эффективный способ поиска и сравнения шаблонов.
Для быстрого поиска шаблонов необходимо ввести некий дескриптор, характеризующий форму контура. При этом, близкие между собой контуры должны иметь близкие дескрипторы. Это избавило бы нас от процедуры вычисления ВКФ контура с каждым шаблоном. Достаточно было бы сравнить только дескрипторы, и если они будут близки – только в таком случае – вычислять ВКФ. Само же сравнение дескрипторов должно быть быстрым. В идеале — дескриптором должно быть одно число.
К сожалению, в литературе, я не нашел явного описания подходящих дескрипторов, описывающих форму контура. Тем не менее, такой дескриптор существует. АКФ инвариантно к переносу, вращению, масштабированию и выбору начальной точки. И кроме того, АКФ является функцией одного контура, а не двух, как ВКФ. Исходя из этого, АКФ можно выбрать в качестве дескриптора, описывающего форму контура. Близкие контуры всегда будут иметь близкие значения АКФ.
Сравнение двух АКФ имеет сложность O(k), что уже значительно лучше чем O(k2) для ВКФ. Кроме того, как мы помним, АКФ из-за симметрии, определено только на интервале от 0 до k/2, что еще в два раза уменьшает время вычислений. Если база шаблонов хранит их АКФ, то поиск шаблона для контура, путем сравнения АКФ, составит O(kt).
3.9 Сверстка автокорреляционной функции
АКФ представляет собой вектор с k/2 значениями. Если вычисляем некую меру различий двух АКФ, нам нужно перебрать все k/2 значений. В принципе, если порог различий фиксирован, то мы можем на каждом шагу вычислять текущую меру различий, и как только она превысит порог – прерывать сравнение АКФ. Таким образом мы ускорим сравнение АКФ. Однако тут есть две сложности – во-первых, вычисление меры на каждом шагу затратно по времени, во-вторых, если различие происходит в середине, или только в последних компонентах значении АКФ, то эффективность данного алгоритма падает, и он вырождается в полное сравнение. Для более эффективного решения проблемы сравнения АКФ, изменим способ представления АКФ. Вместо хранения самой АКФ, будем хранить вейвлетную свертку модулей значений АКФ. При этом первый компонент свертки будет соответствовать наиболее крупномасштабному вейвлету, а последующие компоненты – будут уточнять значения функции во все более мелких масштабах [13].
Вейвлетная свертка позволит нам упорядочить значения АКФ в масштабном порядке. Первым будет идти компонент, отвечающий наиболее крупномасштабным особенностям АКФ, а дальнейшие компоненты будут уточнять все более мелкие особенности АКФ.
Вейвлетная свертка нам дает преимущества при сравнении АКФ. Сравнивая первые компоненты свертки мы получаем сравнение АКФ в наиболее грубом приближении. Если эти компоненты существенно отличаются, дальнейшие сравнения можно не делать, потому что АКФ гарантированно отличаются. Далее, мы сравниваем вторые компоненты свертки, если они существенно отличаются – также прерываем сравнение и так далее. Кроме того, мы можем не сравнивать все k/2 компонент свертки. Поскольку сравнение носит оценочный, приближенный характер, нам достаточно сравнить первые 4-5 значений свертки АКФ. А затем, при их близости, сразу переходить к вычислению ВКФ.
Отметим следующее.
1. Сравнение АКФ, в общем случае, не избавляет нас от необходимости вычисления ВКФ. Только ВКФ дает точную оценку близости контуров. АКФ же, в общем случае, может совпадать для различных контуров. Но, при этом, предварительный отбор шаблонов по АКФ существенно сужает число кандидатов на сравнение по ВКФ.
2. Сравнения АКФ может быть достаточно для идентификации контуров. Если на изображении ищутся маркеры с простой геометрической формой, и вероятность ошибочных распознаваний не существенна, то можно опустить процесс сравнения ВКФ, ограничившись только сравнением сверток АКФ. Такой алгоритм дает наибольшую производительность системы.
3. Первый компонент свертки АКФ дает нам хороший дескриптор для упорядочивания базы шаблонов. Действительно, если для данного контура подходят только шаблоны, у которых первый компонент свертки приблизительно равен первому компоненту свертки контура, то имеет смысл упорядочить шаблоны в базе по первому компоненту свертки. Это сразу на порядок уменьшает число шаблонов-кандидатов на сравнение. Для больших баз шаблонов это может дать хороший прирост производительности.
Теперь остановимся на выборе конкретных вейвлетов для свертки.
В принципе, мы можем использовать любые свертки, у которых первый компонент характеризует функцию в наибольшем масштабе, а последующие – уточняют значение на более мелких масштабах.
Однако, учитывая то, что свертка нам нужна для сравнения, и то, что АКФ часто является симметричной функцией (см рисунки в первой главе), то не все вейвлеты одинаково хорошо подходят для наших целей. Основным критерием к выбору вейвлета является его дискриминирующие свойства. Для примера, рассмотрим широко распространенные вейвлеты Хаара и Уолша: (см.рис.3)
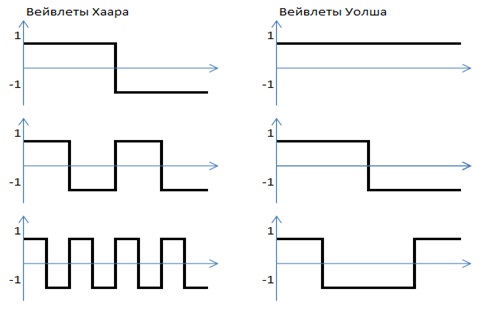
Рисунок 3 – Вейвлеты Хаара и Уолша
Из-за симметричности АКФ относительно центральной линии, первый компонент вейвлета Хаара даст нулевое значение. Второй компонент вейвлета Хаара, также даст нулевое значение, из-за симметричности половинок АКФ относительно своих середин. Кроме того, если мы посмотрим на примеры АКФ, приведенные в первой главе, окажется что первый компонент вейвлета Хаара дает нуль для всех АКФ, кроме последней (контур буквы А). Второй компонент Хаара также даст нуль для контуров круга и квадрата. (см.рис.4)
Одинаковые значения первых компонент говорит о плохих дискриминирующих свойствах вейвлетов Хаара для свертки АКФ.
Теперь рассмотрим вейвлеты Уолша. Первый компонент свертки, по сути, является суммой всех компонент АКФ. Обратим внимание на то, что эта сумма различна для всех примеров АКФ, приведенных в первой главе. Это значит, что дискриминирующие свойства вейвлета Уолша для симметричных АКФ лучше, чем вейвлета Хаара. Первые четыре компонента свертки Уолша обозначены красными столбцами на рисунках АКФ в первой главе.Ниже приведена гистограмма частоты встречаемости первого компонента свертки Уолша для базы шаблонов контуров латинских букв (всего в базе 3463 шаблона).
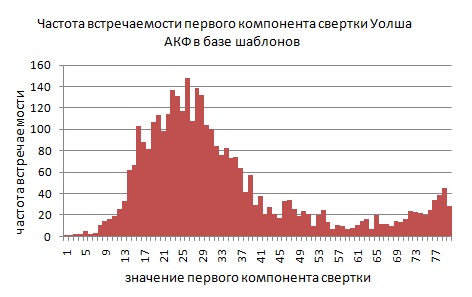
Рисунок 4 – Вейвлеты Хаара и Уолша
Дискриминирующий вейвлет должен давать равномерное распределение для своего первого компонента. Свертка Уолша не дает равномерного распределения, однако ее дискриминирующих свойств первого компонента достаточно для уменьшения пространства поиска шаблонов в три-четыре раза.
На пример, первый компонент контура изображения равен 25 (одно из наиболее часто встречаемых значений в базе шаблонов). Если мы примем пороговую разность сверток Lmax=4, значит, нам подойдут шаблоны в интервале от 21 до 29. Из графика видно, что в этом интервале находится около 1000 шаблонов. Это составляет 1000/3463=29% от всех шаблонов. Значит, в наихудшем случае, сравнение по первому компоненту свертки отфильтрует более 70% неподходящих шаблонов.
В целом, оптимальный выбор вейвлетов определяется характерными формами распознаваемых объектов. Например, если объекты симметричны, лучше выбирать несимметричные базовые функции вейвлетов.
3.10 Эквализация контуров
В реальном же изображении контуры имеют произвольную длину. Поэтому, для поиска и сравнения контуров, все они должны быть приведены к единой длине. Этот процесс называется эквализацией. В литературе описан способ эквализации, дающий на выходе контур, состоящий из заданного числа одинаковых по длине отрезков. Однако этот метод довольно сложен (не будем забывать, что нам нужно будет проводить эквализацию всех контуров изображения, которых в общем случае О(n2)).
Поэтому будем применять более простой и быстрый способ эквализации, который, помимо приведения к единой длине, производит сглаживание контура методом скользящего среднего. Итак, сначала мы фиксируем длину ВК, которую мы будем использовать в нашей системе распознавания. Обозначим ее k. Затем, для каждого исходного контура Г создаем вектор-контур N длиной k. Далее возможно два варианта – либо исходный контур имеет большее число ЭВ чем k, либо меньшее число чем k. Если исходный контур больше необходимого, то перебираем все его ЭВ, и считаем элементы N как сумму всех ЭВ, следующим образом (C#):
Complex[] newPoint = new Complex[newCount];
for (int i = 0; i < Count; i++)
newPoint[i * newCount / Count] += this[i];
Этот алгоритм достаточно грубый, особенно для длин немногим больших k, однако он вполне применим на практике. Если же исходный контур меньше k, то производим интерполяцию, и считаем примерно так:
Complex[] newPoint = new Complex[newCount];
for (int i = 0; i < newCount; i++)
{
double index = 1d * i * Count / newCount;
int j = (int)index; double k = index - j;
newPoint[i] = this[j] * (1 - k) + this[j + 1] * k; }
При малых значениях k (менее 30) — резко повышается число шумовых распознаваний (распознавание как символов шума или других не символьных элементов изображения), снижается число верных распознаваний, и увеличивается число ложных распознаваний. Таким образом, значение k=30 является оптимальным для данной системы распознаваний.
Обратите внимание, что увеличение длины контура, после определенного уровня (25 и выше) вовсе не приводит к улучшению качества распознавания. Это связано с тем, что в описанном методе, эквализация проводится одновременно со сглаживанием контуров. При больших значениях длины, сглаживание становится все более мелкомасштабным, и контур становится слишком детализированным, и следовательно, более отличным от шаблонных контуров [14].
Выводы
В результате выполнения данной работы были рассмотрены и проанализированы следующие задачи:
1) рассмотрены основные принципы построения алгоритмов контурного анализа, которые позволили разработать алгоритм;
2) избран оптимальный алгоритм для написания программного продукта, который максимально точно и за короткое время дает результат;
3) проведен обзор существующих систем;
4) проанализирована оценка производительности алгоритмов контурного анализа, было выявлено, что при современном развитии компьютерной техники, контурный анализ вполне может используемых в качестве алгоритм реального времени;
5) в ходе исследования дескрипторов Фурье выяснилось, что данный вид дескрипторов обладает всем требованиям к классификации: инвариантность относительно поворота, масштабирования и параллельного сдвига. В связи с этим привидение контура к объекту амплитудному Фурье спектру помогает классифицировать данный объект в режиме реального времени.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2015 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список использованных источников
- Фурман Я. А. Введение в контурный анализ. - М.: ФИЗМАТЛИТ, 2003. –561 с.
- Детектирования автомобильных номеров на основе контурного анализа [Электронный ресурс] – Режим доступа: http://mp3car.ru/blog/ComputerVision/15.html
- Цифровая обработка изображений/ Интернет-ресурс. - Режим доступа: www / URL: http://rudocs.exdat.com/docs/index-87395.html - за глав. с экрана.
- Гонсалес Р. Цифровая обработка изображений в среде C # / Р. Гонсалес, Р. Вудс, С. Еддинс - М.: Техносфера, 2006. - 616с.
- Грибков И.В. Некоторые вопросы количественной оценки продуктивности детекторов границ/ И.В. Грибков, А.В. Захаров, П.П. Кольцов и др. - М.: «Программные продукты и системы» № 4, 2011. - 234с.
- Леухин А.Н., доц. Парсаев Н.В., асп.Рахманов Х.Э. Алгоритм локализации изображения регистрационного номерного знака автомобиля с использованием методов контурного анализа [Электронный ресурс] – Режим доступа: http://hpc.marsu.ru/Content/articles/7.pdf
- Алиев М.В., Панеш А.Х., Каспарьян М.С. Выделение контуров на малоконтрастных и размытых изображениях с помощью фрактальной фильтрации [Электронный ресурс] – Режим доступа: http://cyberleninka.ru/article/n/vydelenie-konturov-na-malokontrastnyh-i-razmytyh-izobrazheniyah-s-pomoschyu-fraktalnoy-filtratsii
- Костюкова Н.С., Коршун А.Н., Корольчук Е.А. Выделение контуров объектов в растровых изображениях http://ea.donntu.ru:8080/jspui/bitstream/123456789/15503/1/163-170.pdf
- Потапов А.А., Гуляев Ю.В., Никитов С.А., Пахомов А.А., Герман В.А. Новейшие методы обработки изображений - М.: ФИЗМАТЛИТ, 2008. –489 с.
- Гонсалес Р., Вудс Р. Цифровая обработка изображений Издательство "Мир" Москва 1982 - 312 с.
- Анисимов Б.В., Курганов В.Д., Злобин В.Н. Распознавание и цифровая обработка изображений - М.: ФИЗМАТЛИТ, 2003. –561 с.
- Хуанг Т. Обработка изображений и цифровая фильтрация Перевод с анг. к.т.н. Е.З. Сорокин, В.А.Хлебородова Издательство "Мир" Москва 1979 - 412 с.
- Форсайт Д. Компьютерное зрение. Современный подход. :Перевод с анг. - М.: Издательский дом "Вильямс", 2004. - 928 с.
- OpenCV шаг за шагом. Нахождение контуров и операции с ними [Электронный ресурс]. – Режим доступа: www/ URL: http://robocraft.ru/blog/compute rvision/640.html
