Аннотация
Статья посвящена интерактивным методам удаления невидимых частей трехмерной сцены. Приводится детальное описание процесса построения и обхода BSP-дерева, также доступна для скачивания библиотека на C++ с реализацией алгоритмов BSP-деревьев.
Введение
Двоичное разбиение пространства (BSP - binary space partition) - это метод, который впервые был сформулирован в 1969 году [1]. Изначально предлагалось использовать метод для сортировки полигонов в сцене. В то время отсутствовала аппаратная поддержка буфера грубины (z-buffer), а программная реализация была слишком медленной. Однако метод двоичного разбиения пространства остался актуальным даже после создания аппаратного z-buffer-а (поскольку, к сожалению, метод z-buffer-а не решает многих проблем, например, отображение полупрозрачных объектов). Кроме сортировки, метод широко применяется и в других областях, к примеру, проверка на столкновение, в некоторых алгоритмах компьютерных сетей, в методе излучательности.
Скорость работы метода двоичного разбиения пространства достигается за счёт разбиения исходного пространства и проведения предварительных вычислений. На вход метода поступает набор некоторых объектов (в случае сортировки полигонов в сцене этими объектами являются полигоны), а потом с помощью рекурсивного алгоритма создаётся двоичное дерево таким образом, что можно совершать обход дерева в порядке от более удалённых к менее удалённым или от менее удалённых к более удалённым многоугольникам.
Алгоритм двоичного разбиения пространства
Принцип работы алгоритма заключается в том, что все полигоны пространства (в общем случае n-мерного) разбиваются на группы, лежащие в разных выпуклых подпространствах относительно некоторой гиперплоскости (гиперплоскость - это пространство размерности n-1). Не нарушая общности рассуждений будем рассматривать 2-хмерное простраство (далее сделаем некоторые поправки для 3-хмерного пространства). В этом случае гиперплоскость будет представлять собой прямую линию. Для наглядности рассмотрим пример (Рис. 1):
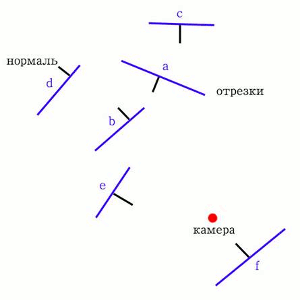
Рисунок 1
У нас есть плоскость (пространство), на которой расположены отрезки (участки гиперплоскостей) с заданными нормалями. Первым этапом алгоритма является определение разделяющей плоскость прямой. Далее будут приведены основные приёмы выбора гиперплоскости, а пока, не вдаваясь в подробности, будем выбирать произвольный отрезок (например, отрезок "b") и дополнять его до прямой - это и будет наша гиперплоскость (Рис.2):
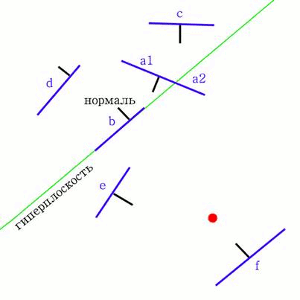
Рисунок 2
Благодаря прямой, мы получили плоскость, разбитую на две полуплоскости. Нормаль к прямой совпадает с нормалью отрезка, через который она проведена. По направлению нормали мы будем определять переднюю и заднюю полуплоскости: если нормаль находится в полуплоскости, то данная полуплоскость - передняя; иначе - задняя. Теперь нужно определить, каким полуплоскостям принадлежат отрезки. Таким образом все отрезки разбиваются на три группы: отрезки, лежащие в передней полуплоскости ("c" и "d"), отрезки, лежащие в задней полуплоскости ("e" и "f"), и отрезки, лежащие на прямой (только "b"). Если отрезок принадлежит обоим полуплоскостям, то он делится на два (так "a" делится на "a1" и "a2"). Если узлу двоичного дерева приписать прямую и все отрезки, лежащие на ней, а две оставшиеся группы приписать его дочерним поддеревьям, то получим образование следующей структуры (Рис. 3):
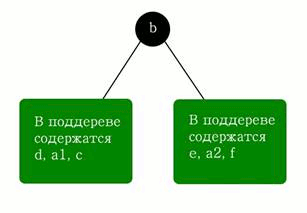
Рисунок 3
Теперь нужно рекурсивно повторить алгоритм для каждого поддерева. То есть, мы имеем в качестве пространства переднее полуподпространство (в него входят отрезки "d", "a1", "c"). Выбираем любой из этих отрезков, например, "a1" и проводим через него гиперплоскость: получаем в качестве переднего поддерева отрезок "d", а заднего - "c" (Рис. 4):
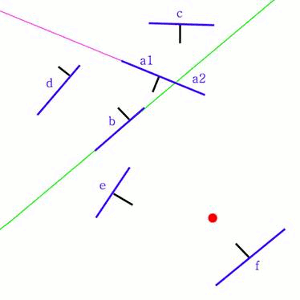
Рисунок 4
Получаем структуру следующего вида (Рис. 5):
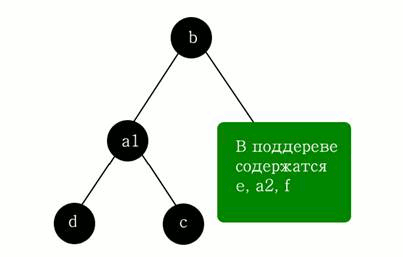
Рисунок 5
Аналогичным образом поступаем с задним поддеревом узла "b". Например, если выбрать за гиперплоскость сначала "a2", а затем "e", то получим следующее разбиение исходной плоскости прямыми (Рис. 6):
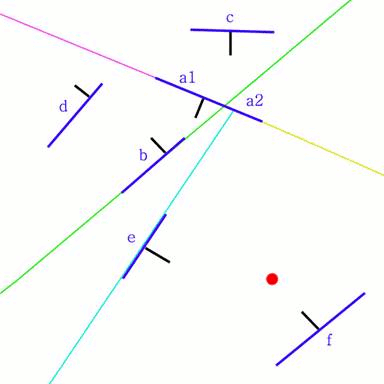
Рисунок 6
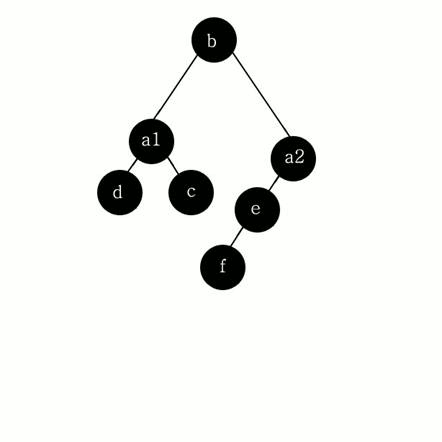
Рисунок 7
Итак, мы построили дерево двоичного разбиения пространства. Теперь можно, зная положение камеры, обойти все дерево по полигонам от самого дальнего до самого ближнего к камере . Начинается обход дерева, естественно, с его корня. Порядок обхода каждого узла задается положением камеры относительно прямой, соответствующей данному узлу, следующими правилами:
- Если камера находится в передней полуплоскости относительно прямой, соответствующей данному узлу, то обходим сначала заднее поддерево, потом все полигоны, которые находятся в данном узле, и в последнюю очередь переднее поддерево.
- Наоборот, если камера в задней полуплоскости, то обходим узел в порядке от переднего поддерева к заднему.
- Если же камера находится на данной прямой, то сначала обходятся поддеревья в любом порядке, а полигоны самого узла не обходятся вовсе (т.к. они, фактически, не видны наблюдателю) или обходятся в последнюю очередь, упорядоченные некоторым образом (например, по расстоянию от дальнего ближнему).
Удаление невидимых поверхностей с помощью BSP-деревьев
Несмотря на то, что на сегодняшний день аппаратно реализован z-buffer, количество полигонов в сцене растёт экпотенциально и интерактивная визуализация таких сцен становится проблематичной, так как только аппаратной поддержки не хватает. Поэтому имеет смысл использовать другие алгоритмы определения видимости в сцене, которые можно использовать вместе с аппаратным ускорением, что повышает скорость визуализации.
Алгоритм Нейлора удаления невидимых поверхностей для статических сцен.
Певым этапом алгоритма Нейлора является построение BSP-дерева. Далее делается обход дерева сверху вниз от ближнего полигона к дальнему. При этом для каждого полигона делается проекция его на экранную плоскость. Рекурсивный процесс обхода и вывода прекращается, когда всё поддерево будет перекрыто предыдущим спроектированным полигоном. Для лучшего понимания рассмотрим пример (Рис. 8)
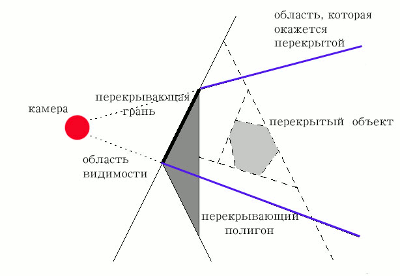
Рисунок 8
В случае статической сцены BSP-дерево можно было построить один раз и при изменении положения камеры исходное дерево обходилось начиная с того корня и в том порядке, как это было нужно. Когда же в сцене присутствуют динамические объекты (которые меняют форму или положение), то построенное в начале дерево становится непригодным, поэтому естественным предположением решения этой задачи является его перестраивание в каждый момент времени. Однако для интерактивной визуализации этот способ является неприемлемым, поскольку построение BSP-дерева процесс длительный (так как количество полигонов исчисляется тысячами и более), поэтому нужны способы, которые минимизируют количество обновлений BSP-дерева.
Одним из таких способов является метод временных ограничивающих объёмов [2]. Этот метод может являться дополнением для любого алгоритма удаления невидимых поверхностей в статических сценах. Изначально все объекты сцены (состоящие из полигонов) разбиваются на две группы - статические и динамические. Для статических строится отдельное дерево и это дерево обрабатывается посредством, например, алгоритма Нейлора или любого другого аналогичного алгоритма. Для каждого динамического объекта строится объём (на основе знания о поведении динамического объекта - например, траектории движения), который гарантировано будет содержать данный объект в течении некоторого промежутка времени. Далее строится BSP-дерево, но в узлы вставляются не полигоны объекта, а полигоны ограничивающего объёма. Динамический объект игнорируется пока не истечёт время действия его ограничивающего объёма, либо пока его ограничивающий объём не станет видимым.
Плюсами этого алгоритма является то, что во-первых, не нужно обновлять BSP-дерево в каждый момент времени, а во-вторых то, что динамический объект аппроксимируется упрощённой геометрической формой (эллипсоидом, либо кубом).
Недостатки алгоритмы очевидны - мы не может создать универсальную библиотеку, которая позволяла бы строить временные ограничивающие объёмы для совершенно любой сцены с любой динамикой. Ещё одной проблемой является выбор времени в течении которого будет действовать ограничивающий объём (особенно проблема становится актуальной для сцены с произвольной динамикой). И последней проблемой является то, что когда мы ограничиваем объект упрощённым объёмом (сферой или кубом), то есть большая вероятность потерять часть полигонов, которые могут быть не осечены, либо, что хуже, отсечены, когда этого делать не следует.
В заключение можно сказать, что задача реализации удаления невидимых объектов для статических сцен хорошо решается с помощью BSP-деревьев, тогда как динамические сцены требует обновления BSP, что может занимать существенное время и без применения дополнительных алгоритмов (в частности, временных ограничивающих объемов) неприменимо в реальных приложениях.
Список использованной литературы
1. Shumacker, R., Brand, R., Gilliland, M., Sharp, W. Study for Applying Computer-Generated Images to Visual Simulation
2. Sudarsky, C. Gotsman. Dynamic scene occlusion culling. IEEE Transactions on Visualization and Computer Graphics, vol. 5 no.1, January - March 1999.