Аннотация
Thömas Moller, Ben Trumbore. Быстрое нахождение пересечения луча и треугольника. Рассмотрен и описан метод нахождения пересечения луча и треугольника, не требующий знания уравнения плоскости треугольника.
Введение
Пусть луч 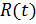 с центром в точке
с центром в точке 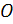 и единичным вектором направления
и единичным вектором направления 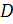 определен как
определен как
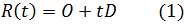
и треугольник определен тремя вершинами 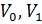 ,
, 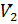 . В задаче нахождения пересечения луч/треугольник мы хотим определить пересекается ли луч с треугольником. Предыдущие алгоритмы решали это вычисляя пересечение между лучом и плоскостью, в которой лежит треугольник, а потом проверяя лежит ли точка пересечения внутри его границ [?].
. В задаче нахождения пересечения луч/треугольник мы хотим определить пересекается ли луч с треугольником. Предыдущие алгоритмы решали это вычисляя пересечение между лучом и плоскостью, в которой лежит треугольник, а потом проверяя лежит ли точка пересечения внутри его границ [?].
Наш алгоритм использует минимум хранимой информации (должны храниться только вершины треугольника) и не требует предварительной обработки. Для треугольных сеток это дает значительный выигрыш в памяти, от около 25% до 50%, в зависимости от того насколько соседние треугольники делят информацию о вершинах.
В нашем алгоритме к центру луча применяется преобразование. Преобразование дает вектор, который содержит расстояние до пересечения - и координаты пересечения - 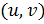 . Таким образом поиск пересечения луча и треугольника предыдущими алгоритмами не используется. Следует отметить, что этот метод был известен ранее, например в [?] и [?].
. Таким образом поиск пересечения луча и треугольника предыдущими алгоритмами не используется. Следует отметить, что этот метод был известен ранее, например в [?] и [?].
Алгоритм нахождения пересечения
Пусть точка на треугольнике 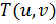 записана как:
записана как:

где 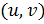 – это барицентрические координаты, которые должны удовлетворять условиям:
– это барицентрические координаты, которые должны удовлетворять условиям:  и
и 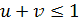 . Заметим, что
. Заметим, что 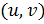 могут быть использованы для отображения текстуры, интерполяции нормали, цвета и т.д. Вычисление точки пересечения луча
могут быть использованы для отображения текстуры, интерполяции нормали, цвета и т.д. Вычисление точки пересечения луча 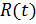 и треугольника
и треугольника 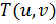 эквивалентно решению уравнения
эквивалентно решению уравнения 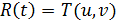 , которое запишется как:
, которое запишется как:
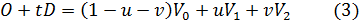
Перегруппировав члены, получим:
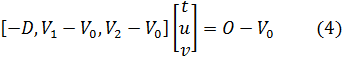
Это значит, что барицентрические координаты 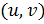 и расстояние
и расстояние  от начала луча до точки пересечения может быть найдено из решения системы линейных уравнений выше.
от начала луча до точки пересечения может быть найдено из решения системы линейных уравнений выше.
Преобразование выше может геометрически восприниматься как перемещение треугольника к началу координат и трансформация его в единичный треугольник на осях 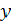 и
и 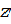 , направление же луча при этом будет совпадать с осью , как показано на рисунке 1 (где
, направление же луча при этом будет совпадать с осью , как показано на рисунке 1 (где 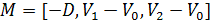 это матрица в уравнении 4).
это матрица в уравнении 4).
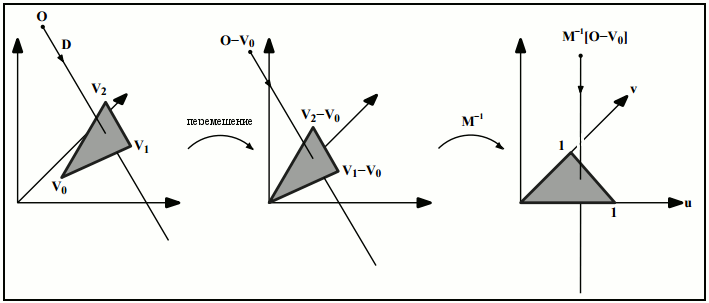
Рисунок 1 – Преобразование начала луча
Аренберг в [?] описывает алгоритм подобный представленному выше. От также строит матрицу 3х3, но использует нормаль треугольника вместо направления луча 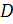 . Этот метод требует хранения нормали для каждого треугольника или вычисления ее на ходу.
. Этот метод требует хранения нормали для каждого треугольника или вычисления ее на ходу.
Обозначим 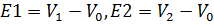 и
и 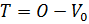 , решение уравнения (4) получим по правилу Крамера:
, решение уравнения (4) получим по правилу Крамера:
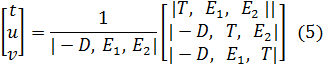
Из линейной алгебры мы знаем, что 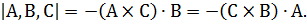 Уравнение (5) может быть записано как:
Уравнение (5) может быть записано как:
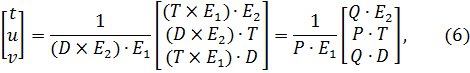
Где 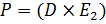 и
и 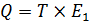 . В нашей реализации мы сохраняем и используем заново эти коэффициенты для ускорения вычислений.
. В нашей реализации мы сохраняем и используем заново эти коэффициенты для ускорения вычислений.
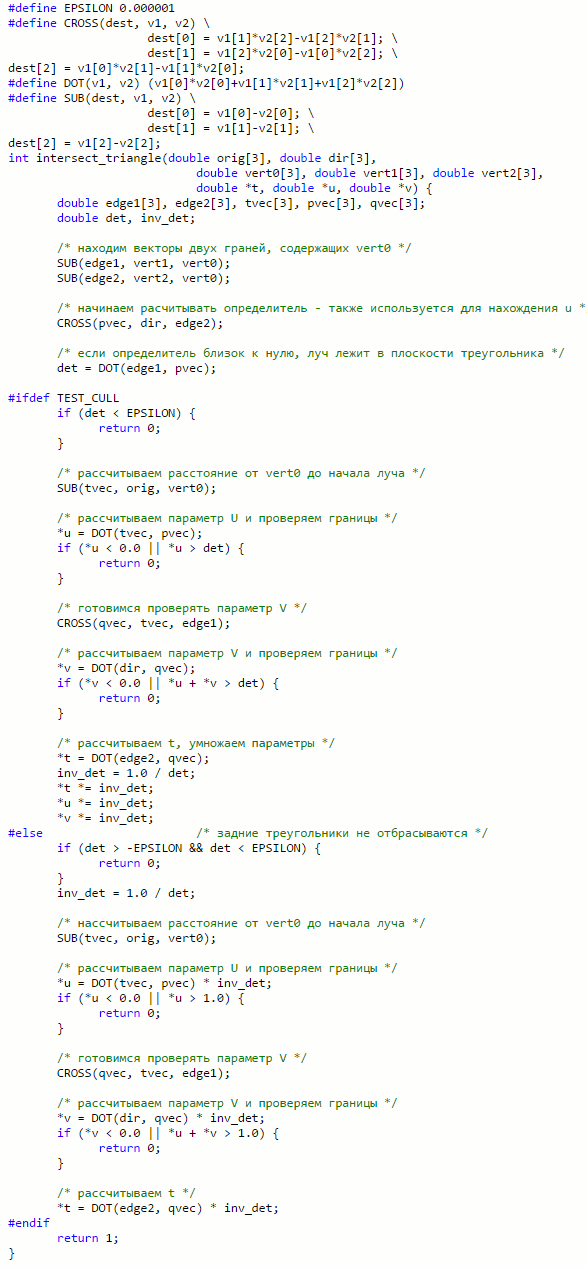
Реализация
Следующая реализация на языке С была приспособлена для оптимальной производительности. В коде два ответвления; одно из которых эффективно отсекает треугольники повернутые задней стороной (#ifdef TEST_CULL), а другое позволяет находить пересечения с двухсторонними треугольниками (#else). Все расчеты отложены до тех пор пока они достоверно не понадобятся. Например, значение не вычисляется пока не будет известно, что находится в допустимых пределах.
Процедура нахождения пересечения с односторонним треугольником отбрасывает все треугольники, для которых определитель (det) отрицателен. Это позволяет отложить единственную операцию деления пока пересечение не подтверждено. Для лучей, рассчитывающих область тени, деление вообще не нужно, так как все что нужно знать – было пересечение или нет.
Процедура нахождения пересечения с двухсторонним треугольником принудительно производит операцию деления с целью нахождения значений 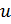 и
и 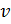 . Эта процедура может быть переписана, чтобы сравнивать значения
. Эта процедура может быть переписана, чтобы сравнивать значения 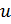 и
и 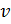 с нулем в зависимости от знака det.
с нулем в зависимости от знака det.
Некоторые аспекты этого кода требуют особого внимания. Расчет реберных векторов можно перенести на стадию предварительной обработки, сохраняя edge1 и edge2 вместо vert1 и vert2. Ускорение будет достигнуто только в случае если пространственное положение vert1 и vert2 не нужно для прочих расчетов, и когда данные о положениях вершин не являются общими между треугольниками.
Чтобы убедиться в численной устойчивости, проверка, которая отбрасывает лучи параллельные плоскости треугольника должна сравнивать определитель с маленьким числом, близким к нулю. Если правильно выбрать значение EPSILON, то этот алгоритм становится очень устойчив. Если необходима проверка только треугольников повернутых “лицевой” стороной, то определитель может проверяться на условие нахождения между 0 и EPSILON (отрицательный определитель свидетельствует, что треугольник повернут задней стороной к лучу).
Значение 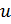 сравнивается с ребром треугольника
сравнивается с ребром треугольника 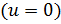 и с линией, параллельной ребру, но проходящей через противоположную точку треугольника
и с линией, параллельной ребру, но проходящей через противоположную точку треугольника 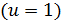 . Хотя на самом деле не сравнение с ребром, а именно вторая проверка отсеивает много точек пересечения из дальнейшего расчета.
. Хотя на самом деле не сравнение с ребром, а именно вторая проверка отсеивает много точек пересечения из дальнейшего расчета.
Результаты
В [?] процедура нахождения пересечения также рассчитывает барицентрические координаты. Мы сравнили этот метод с нашим. Было реализовано два не отсекающих метода в эффективном трассировщике. Рисунок ?? представляет время выполнения на рабочей станции Hewlett-Packard 9000/735 для трех моделей. В данной конкретной реализации, производительность двух методов была примерно соизмеримой.

Рисунок 2 – Время выполнения
Выводы
Мы представили алгоритм нахождения пересечения, который соизмерим по скорости с предыдущими методами, и который требует при этом значительно меньших затрат памяти на хранение, избегая хранения коэффициентов уравнения плоскости.
Список использованной литературы
1. Jeff Arenberg, Re: Ray/Triangle Intersection with Barycentric Coordinates, in Ray Tracing News, edited by Eric Haines, Vol. 1, No. 11, November 4, 1988, http://www.acm.org/tog/resources/RTNews/
2. Didier Badouel, An E_cient Ray-Polygon Intersection, in Graphics Gems, edited by Andrew S. Glassner, Academic Press Inc., 1990, pp. 390-393.
3. Eric Haines, Point in Polygon Strategies, in Graphics Gems IV, edited by Paul S. Heckbert, AP Professional, 1994, pp. 24-46.
4. Edward Patel, personal communication, 1996.
5. Peter Shirley, personal communication, 1996.