Влияние ионосферы

Применительно к ионизированному газу фазовый показатель преломления может быть подсчитан по следующей приближенной формуле:

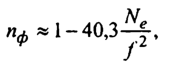
где N_e - концентрация электронов, выражаемая через число свободных электронов в единице объема;f - частота проходящего через ио- носферу радиосигнала.

В связи с тем, что со спутника наряду с несущими гармоническими колебаниями передаются также и кодовые сигналы с использованием процесса модуляции, при реализации которого формируется группа волн, то для нее используется понятие групповой скорости v_гр, а также связанного с ней группового показателя преломления n_гр. Соотношение между фазовым и групповым показателями преломления устанавливается на основе модифицированной формулы Рэлея:

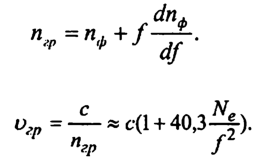
Из совместного рассмотрения формулы 3 и формулы 4 следует, что

Полученные результаты свидетельствуют о том, что в ионизированном газе фазовый показатель преломления n_ф всегда меньше единицы, т.е. фазовая скорость в такой среде больше скорости света в вакууме, а следовательно, гармонические несущие колебания проходят через ионосферу не с замедлением, а с ускорением. Что касается групповой скорости, то она точно на такую же величину отличается от скорости света в вакууме, но в другую сторону, т.е. в сторону занижения. При этом данная скорость характерна для кодовых сигналов, на основе которых производят измерения псевдодальностей.

Величина интересующих нас ионосферных задержек определяется величиной уклонения соответствующего показателя преломления от единицы. С учетом приведенных выше закономерностей изменения показателей преломления ионосферная задержка описывается соотношением вида:

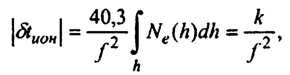
где h — длина пути, проходимого радиосигналом в ионосфере; к — коэффициент пропорциональности, величина которого зависит от концентрации электронов и от длины пути в ионосфере, что, в свою очередь, приводит к зависимости от широты точки стояния, времени суток, сезона года и даты в пределах 11-летнего цикла солнечной активности.

Ионосферные задержки обычно пересчитываются в поправки к псевдодальностям. Их значения оцениваются величинами, лежащими в пределах от 5 до 50 м.

Для предрасчета ионосферных задержек радиосигналов применительно к спутниковым измерениям предпринимались неоднократные попытки создания соответствующих моделей, позволяющих произвести оценку величины таких задержек на момент измерений для конкретных условий наблюдений. Среди различных моделей такого типа наибольшее распространение получила модель, разработанная Дж. А. Клобушаром. Исходными предпосылками в данной модели были приняты предположения о том, что в ночное время уровень ионизации, а следовательно, и временные задержки в ионосфере остаются неизменными по своей величине, а в дневное время эти задержки описываются косинусоидальной функцией, для которой нужно знать амплитуду, период и начальную фазу. Формулы, на основе которых под- считываются поправки за влияние ионосферы, имеют при этом следующий вид:

для дневных наблюдений:

для наблюдений в ночных условиях:

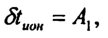
где А₁ - величина ионосферной задержки в ночное время, которая для используемого в GPS частотного диапазона принимается равной 5*10^-9 с; А₃ - фаза используемой косинусоидальной функции, отнесенная к 14 часам местного времени; t_M - местное время; А₂ - амплитуда косинусоидальной функции, для нахождения которой используется полином:

А₄ — период косинусоидальной функции, определяемый на основе использования полинома:

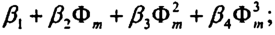
Все альфа и бета - константы, которые определяются ежесуточно с помощью станций слежения, входящих в сектор управления и контроля, и через загружающие станции в составе навигационного сообщения передаются на спутники, которые затем сбрасываются по радиоканалу потребителям; Ф_m — геомагнитная широта «ионосферной точки».

На рис. 1 в графическом виде представлена описываемая уравнением 7 модель Клобушара. Интересующие потребителя ионосферные поправки вычисляются при этом в такой последовательности:

1. Зная приближенные значения широты и долготы точки стояния, а также положение спутника в пространстве, представляется возможным вычислить угол возвышения и азимут линии визирования, ориентированной на спутник;

2. Принимая среднюю высоту ионосферы равной 350 км, вычисляется широта и долгота точки пересечения упомянутой выше линии визирования с ионосферой ("ионосферная точка");

3. Задаваясь географическими значениями широты и долготы «ионосферной точки», определяют угол между этой точкой и геомагнитным северным полюсом Земли. Вычитая полученное значение угла из 90°, находят интересующее значение геомагнитной широты Ф_m, на основе которого могут быть вычислены амплитуда A₂ и половинное значение периода A₄косинусондальной функции. Оба эти параметра представляют собой полиномы третьего порядка от геомагнитной широты «ионосферной точки», причем в состав этих двух полиномов вхо- дят 8 коэффициентов, значения которых сбрасываются по радиоканалу в составе навигационного сообщения;

4. Используя упомянутую выше информацию, с помощью урав- нения 7 может быть вычислена ионосферная задержка в зенитном направлении. На заключительной стадии эта задержка увеличивается за счет введения соответствующего масштабирующего коэффициента, учитывающего наклонное падение радиолуча на ионосферу. Этот коэффициент является функцией угла возвышения линии визирования, ориентированной на спутник. При его расчете приходится принимать во внимание высоту «ионосферной» точки над земной поверхностью, которая определяется недостаточно надежно

Описанный выше метод учета влияния ионосферы считается недостаточно надежным и не обеспечивает высокую точность измерений. В связи с этим он применяется преимущественно в навигации при абсолютных методах координатных определений.

При геодезическом использовании спутниковых измерений наибольшее распространение получил метод учета влияния ионосферы, базирующийся на применении двух несущих частот L1 и L2. Поскольку данный метод заслуживает повышенного внимания при высокоточных геодезических спутниковых измерениях, то изложим вкратце обоснование двухчастотного принципа исключения ионосферных задержек применительно к фазовым измерениям.

Для упрощения математических выкладок пренебрежем на дан- ной стадии влиянием тропосферы, т. е. предположим, что влияние атмосферы сводится только к воздействию ионосферы на результаты спутниковых фазовых измерений.

Из совместного решения уравнений 11 имеем:

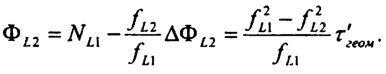
Характерная особенность введенного значения фазового сдвига, относящегося к комбинационной частоте состоит в том, что оно оказывается свободным от влияния ионосферы.

При практических расчетах во многих случаях вводят понятие фактора R=f_L2/f_L1, который для системы GPS имеет следующее число- вое значение:

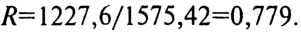
С учетом фактора R может быть получена формула:

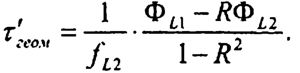
Если отнести эту величину к основной несущей частоте f_L1 то выражение для свободного от ионосферного влияния фазового сдвига принимает вид:

Величина ионосферной поправки может быть при этом подсчитана по формуле:

Аналогичные соотношения могут быть получены и для второй несущей частоты L2.

Приведенные выше математические выкладки свидетельствуют о том, что на основе выполнения измерений на двух несущих частотах представляется возможным не только вычислить практически свободную от влияния ионосферы величину измеряемого до спутника расстояния, но и определить значение ионосферной поправки. Остаточное ее воздействие на результаты измерений обусловлено, главным образом, недостаточно строгим модельным представлением зависимости ионосферной поправки от частоты.

Дополнительное ослабление влияния ионосферы удается достичь за счет использования дифференциальных методов измерений, одна из особенностей которых проявляется в том, что при окончательных расчетах используются не абсолютные значения ионосферных задержек, а их разности, характерные для траекторий радиолучей, соединяющих спутник с двумя разнесенными на местности станциями. Кроме того, наиболее точные работы рекомендуют выполнять в ночное время, когда влияние ионосферы существенно уменьшается.

Из анализа приведенных выше различных подходов, ориентированных на ослабление влияние ионосферы, следует, что наиболее эффективными мерами борьбы с влиянием ионосферы являются методы, базирующиеся на двухчастотных дифференциальных фазовых измерениях, которые открывают возможность измерения на местности линий различной протяженности на сантиметровом (и даже на миллиметровом) уровне точности.