Resume Abstract

Abstract

Contents

• Introduction
• 1. Theme urgency
• 2. Goal and tasks of the research
• 3. A review of research and development
• Conclusion
• References

Introduction

Much attention is paid to questions of adjustment of geodetic networks. They are used at the solution of a problem of estimation of deformations, when adjustment the photogrammetric constructions, in problems of optimization of networks. As an example of effective application of high-rise networks it is possible to give a task of the analysis of stability of reference points of a high-rise basis.

It is also necessary to note that from a position of system approach of a network represent more complete construction whereas networks not free are their special cases. Therefore sometimes to equalize expediently geodetic networks as free, and then to turn in not free, fixing any basic data.

There are many methods for receiving estimates of accuracy when adjustment geodetic networks, for example: method of the smallest squares, Cauchy's method, method of the smallest modules, method of the smallest modules, minimax method, method of the smallest positive square forms, etc.

1. Theme urgency

It is known that creation of engineering and geodetic networks differs in a number of the features caused by that their design is carried out for concrete object (often in the built-up territory). In difference from it is general geodetic networks engineering and geodetic networks have a difficult configuration, are characterized by violation of the geometrical requirements imposed to geodetic networks. Besides accuracy in the engineering and geodetic networks providing carrying out in nature of separate elements of designs increases in process of specification of object under construction. All above-mentioned aspects cause need of wide use for engineering and geodetic practice of free geodetic networks. Therefore research of accuracy of creation of engineering and geodetic networks is actual.

2. Goal and tasks of the research

Purpose and research problems: to compare estimates of accuracy which can be received when adjustment geodetic networks Cauchy's by method and by method of the smallest squares.

For identification of the most effective comparison and the analysis of adjustment Cauchy's method and method of the smallest squares carries out the following practical tasks:

1. Adjustment of uniformally precise measurements, comparison and analysis of results;
2. Adjustment of not uniformally precise measurements , comparison and analysis of results;
3. Adjustment of a geodetic network, comparison and analysis of results.

Object of research : engineering and geodetic networks.

Object of research : Adjustment of engineering and geodetic networks earlier poorly studied Cauchy's by method and comparison of results with method of the smallest squares.

Within a master's thesis receiving actual scientific results in the following directions is planned:

1. Analysis of ways of adjustment of engineering and geodetic networks.
2. Definition optimum way of adjustment of engineering and geodetic networks.
3. Influence on results of estimates by errors of different types of distribution.

3. A review of research and development

Now the increasing attention to questions of adjustment of geodetic networks is paid. First of all we will explain that we will understand as a geodetic network in the context of this work.

The geodetic network is a system of the points (geodetic points) fixed on a surface of the earth and mutually certain on the card / rather existing objects in the plan and for height.

There are different methods of creation of networks.

At creation of planned networks separate points of a network serve initial - their coordinates have to be known. Coordinates of other points define by the measurements connecting them with initial. Planned geodetic networks create by the following methods.

A triangulation – a method of definition of planned provision of geodetic points by construction on the district of a network of triangles in which measure corners, and also lengths of some parties called by the basic parties (fig. 1).



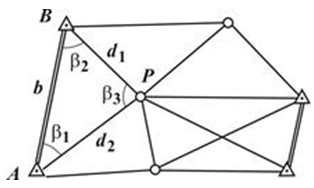
Figure 1. – Scheme of a network of a triangulation

Continuing in this way, calculate lengths of all parties of a network. If, except basis of b other bases (in fig. 1 bases are shown by the double line) are known, lengths of the parties of a network can be calculated with control.

Coordinates of point P will be determined by formulas of a direct geodetic task. Similarly calculate coordinates of all other points.

Trilateration – a method of definition of planned provision of geodetic points by construction on the district of a network of triangles in which measure lengths of their parties.

If in a triangle of AVR (fig. 1) the basis is known and the parties, on the basis of the theorem of cosines are measured, it is possible to calculate triangle corners. Also calculate corners of all triangles, and then, as well as in a triangulation, – coordinates of all points.

Polygonometry – a method of definition of planned provision of geodetic points by a prolozheniye of the broken line (the poligonometrichesky course) or system of the broken lines (polygonometry network) connected among themselves in which measure angles of rotation and lengths of the parties.



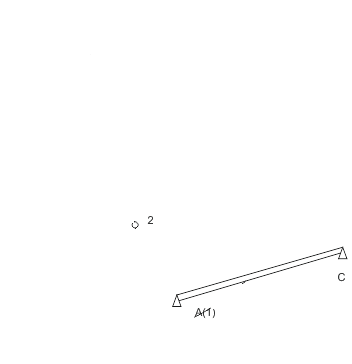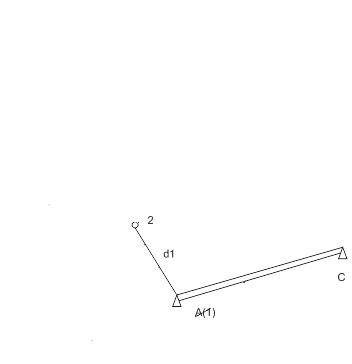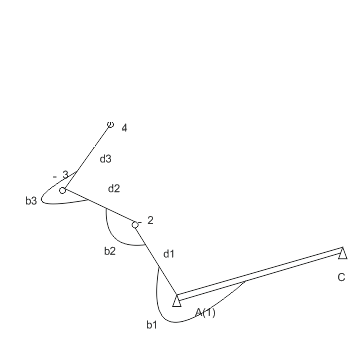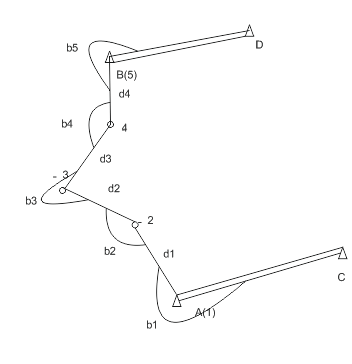
Figure 2. – Creation of a network of polygonometry (animation: 5 frames, 10 cycles of repetition, 20 Kb)


The scheme of the poligonometrichesky course is shown in fig. of 2 a, where to A and B – starting points; CA and BD – the initial directions, which directional corners are known; 1, 2, 3, 4, 5–points (top) of the course; b – the measured horizontal corners; d – the measured lengths of the parties (i = 1, 2, …).

The satellite method of determination of coordinates of geodetic points is based on measurements on signals of satellites of the GLONASS navigation systems (Russia) and GPS (USA) which are carried out by two (and more) by land receivers. By results of measurements with high precision define differences of dx, dy, dz of geocentric coordinates between points. If coordinates of one of points are known, that, having added to them the measured differences, find coordinates of other points. Then coordinates will transform to the geodetic or flat rectangular [9].

What method there would be no coordinates of points that they bear in themselves mistakes. For an exception of mistakes also equalize geodetic networks. For adjustment of geodetic networks make with unknown estimates to matrix coordinates with coefficients of scales near unknown and free members.

We will consider two methods of adjustment of geodetic measurements: Cauchy's method and method of the smallest squares.

Method of processing of geodetic measurements of Cauchy

We will consider the scheme of adjustment on elements. For simplicity and without violation of a community we will put X0=0 so the system of the fundamental equations will assume an air.

Y = L – D = XA,

where Y – a matrix of free members,

X – a matrix of coefficients at unknown,

A – a vector a column of unknown.

Or, in more detail,

yr = lr – dr = [Хrj aj] (r = 1, 2,….N) (1.1)

Supervision are assumed by the uniformally precise. We saw, what at a normality of a vector of errors? the method of the smallest squares has some extreme properties among a wide class of other methods so its application in this sense is favorable. But in the computing relation the decision of system of the normal equations, despite usually applied simplifying receptions, still represents difficulties. Therefore sometimes resort and to other methods estimating aj on supervision of lr (r = 1, 2 …, N) and to the fundamental equations.

Drawing up the normal equations and receiving with their help of estimates for parameters (a1, …., and n) there is, eventually, a method of such combination of N equations with errors of excess system that it was as a result possible to receive solvable system of the linear equations concerning n of parameters (a1, …., and n). Such methods can be much, besides a method of the smallest squares. Though as it is explained above, they will already not have the extreme properties inherent in a method of the smallest squares. One of such methods was offered O. Cauchy.

Here we will state in brief its contents.

Forward stroke. O. Cauchy's instruction is as follows. At first the system (1) is prepared, i.e. multiplication of each equation on +1 or–1 achieve what x1j>0 (j = 1,2 …. N). We will assume that it is already made. Further, all equations develop so it turns out

(h11 + h21 … + xN1) a1 + (x12+x22 + … + xN2) a2 + …. + (x1n + x2n + … + xNn) an=y1 + … + yN.

We will adhere to Cauchy's designations, believing

x1j+x2j + … + xNj=Sxj (j = 1,2, …, n)

We have then

a1Sx1 + … + anSxn =Sy

Owing to previous, Sx1>0. Dividing into Sx1, we receive:

a1 + a2 * S _ (x_2)/S _ +an (x_2) * S _ (x_n)/(Sx_1) = Sy / (Sx_1) (1.2)

We multiply (1.2) respectively on h11, h12 …. x1N is also deductible from the received N equations the equation of system (1.1); then the members containing a1 disappear and the system from N equations with (n – turns out 1) unknown a2, …., an

(x12 – x11 (Sx_2)/(Sx_1)) a2 + … + (xnn – x11 (Sx_n)/(Sx_1)) an = y1 – x11 Sy / (Sx_1),

(xN2 – xN1 (Sx_2)/(Sx_1)) a2 + …. + (xNn – xN1 (Sx_n)/(Sx_1)) an = yN – xN1 Sy / (Sx_1)

Further, we prepare also new system and we make with it the same operations. Eventually, generally speaking, we receive system N of the equations with one unknown an

x'rnan = y'r (r = 1, 2,…., N);

where xrn'> 0 – the turned–out coefficients, and y'r – linear combinations from yq (q = 1, 2, …. N), turned out in the course of work.

Further, we replace in each of y'r yq unknown to us on known and we observe yq. Result of such replacement we will designate l'r. After that we find a'n from the equations

a'n = (Sl_r)/(Sx_(r ) )

Reverse motion. We set up the last unknown in a matrix (1.1), we leave unknown in the left member of equation, and we transfer known elements to the right part and we apply the same formulas, as in a forward stroke until we find all unknown elements. We form a vector a column of the found unknown [2].

Method of processing of geodetic measurements method of the smallest squares

There are two approaches to the solution of a problem of adjustment. We will consider them in essence.

1. We will take a triangle where all three corners (fig. 3) are measured. Therefore, the equation takes place

b1+v1+b2+v2+b3+v3–180=0

where b – the measured corners, v – amendments.



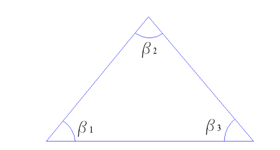
Figure 3. – A triangle where all three corners are measured

Having designated:

b1+b2+b3–180=W

where W – not knitting in a triangle, we can write down

v1+v2+v3+W=0. (2.1)

In (2.1) v1, v2, v3 – unknown, and W – the free member.

We received one equation with three unknown which has a set of decisions, i.e. the system is uncertain.

2. We will take system of three leveling courses with one nodal point (fig. 4.). Thus height of a nodal point of H will be unknown.

Having designated:

b1+b2+b3–180=W

where W – not knitting in a triangle, we can write down

v1+v2+v3+W=0. (2.1)

In (2.1) v1, v2, v3 – unknown, and W – the free member.

We received one equation with three unknown which has a set of decisions, i.e. the system is uncertain.

2. We will take system of three leveling courses with one nodal point (fig. 4.). Thus height of a nodal point of H will be unknown.



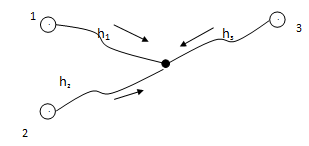
Figure 4 – System of three leveling courses with one nodal point

Therefore, it is possible to write down three equations

H–H1–h1=v1

H–H2–h2=v2 (2.2)

H–H3–h3=v3

where Hi – heights of initial reference points, H – height of a nodal point, hi – measured excess.

Thus, we have three equations with one unknown N. Sledovatelno, we again received uncertain system.

Principle of the smallest squares and its justification.

The essence of the decision on the principle of the smallest squares consists that systems decide under a condition

[pvv] =min (2.3)

where р – the weight of measurements, i.e. under a condition of a minimum of the sum of squares of the amendments increased on the weight of measurements. In case of uniformally precise measurements (2.3) assumes an air:

[vv]=min

We will consider the solution of a problem of adjustment on this way on the example of system (2.2).

We will present (2.2) in the form:

H–l1=v1

H–l2=v2

H–l3=v3

where li=Hi+hi (i=1,2,3), also we will substitute in (2.3).

f (H) =p1v1v1+p2v2v2+p3v3v3=p1 (H–h1) ^2+p2 (H–h2) ^2+p3 (H–h3) ^2

To find a minimum of function f (H) we will take a derivative on the hi variables and we will equate it to zero.

f' (H) =2p1 (H–h1) +2p2 (H–h2) +2p3 (H–h3) =0

or

2H (p1+p2+p3) of–2 (h1p1+h2p2+h3p3) =0

As a result we will receive:

H = [ph] / [p] (2.4)

Expression (2.4) represents the general arithmetic middle [5].

To be convinced that the decision (2.4) really gives at least (2.3), we will find the second derivative:

f' (H) =2p1+2p2+2p3=2 [p]> 0

The second derivative is positive. Therefore,

f (H) = =min [pvv]

We will sum up the result:

1. We received the only decision of system (2.2). Thus it appeared the general arithmetic middle that confirms unity of the principle of the smallest squares and the principle of the arithmetic middle.

2. From (2.3) and (2.4) follows that the decision (2.4) corresponds to a minimum of function (2.3) and according to a minimum of an empirical average quadratic error of a unit of weight:

mm = [pvv]/(n–1)

Therefore, the weight of the determined size equal:

PH=c[p]/mm

where with – any positive constant.

At any values with, [p] of PH will be maximum [6].

Therefore the solution found by way of the smallest squares corresponds to the greatest weight of the determined size.

In relation to two approaches, formulated by us in 2.2 in the form of the equations (2.2) and (2.1) there are two ways of adjustment:

1. Parametrical way

2. A way of adjustment of the measured sizes connected by conditions [3].

Parametrical way of adjustment.

Let for determination of values of unknown x, y, z,… t are executed uniformally precise independent measurements of L1,L2., Ln. Total number of unknown t, total number of measurements of n. At what n> t, i.e. system uncertain.

Coordinates of points, heights of reference points and other sizes which values need to be defined can be unknown.

The horizontal directions, horizontal or vertical angles, lengths of lines, excess, etc.

Between unknown x, y, z … t and the measured sizes Li exist exact mathematical dependences which can be presented in a general view:

fi (x, y, x., t) =Li+Vi (2.5)

where Vi – amendments to the measured Li values.

On the basis of (2.5) we will be able to write down system of the equations of amendments to a general view:

f1 (x, y, x., t) – L1=V1

f2 (x, y, x., t) – L2=V2 (2.6)

.........................

fn (x, y, x., t) – Ln=Vn

Before adjustment of the equation (2.6) it is necessary to lead to a linear look. For this purpose we will enter approximate values of unknown x0, y0, z0., t0 and amendments to these approximate values dx, dy, dz., dt i.e.

x=x0+dx

y=y0+dy

z=z0+dz (2.7)

..........

t=t0+dt

We will substitute (2.7) in (2.6)

fi (x0+dx, yo+dy, z0+dz., to+dt) – Li=Vi (2.6a)

We will spread out the fi function in a row of Taylor, being limited only to the first degrees of amendments. As a result we will receive:



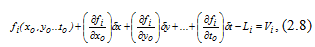
Figure 5.–Decomposition in a row Taylor of the fi function

where i = (1,2., n)

We will enter designations:



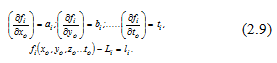
Figure 6.–Designations

Taking into account (2.7), (2.8), and (2.9) system of the equations of amendments (2.6) assumes an air:



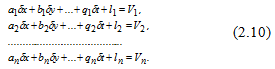
Figure 7.–System of the equations of amendments

Total number of the equations of amendments equally to number of measurements of n [8].

We will take system of the equations of amendments to a linear look. That calculations were not such bulky, we will be limited only to three unknown, meaning that the received results can be extended to any number of unknown. So,



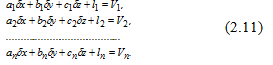
Figure 8.–System of the equations of amendments with three unknown

The number of the equations are more than number of unknown. Number of the equations of n, number of unknown 3. Number of excess measurements of r = n – 3, and therefore the system (2.11) has no only decision.

We will find a minimum [vv] for this system. We will square the left and right parts of the equations of amendments (2.11), and we will put results.



Figure 9.–Stay [vv]

To find a minimum [vv], we will take from function (2.12) private derivatives on unknown dx, dz, dz and we will equate them to zero



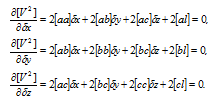
Figure 10.–Private derivatives on unknown

Having reduced by the general multiplier 2, we will receive



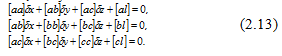
Figure 11.–Private derivatives on unknown reduced on 2

The number of unknown is equal in system (2.13) to number of the equations. Such system has the only decision. That is why (2.13) it is accepted to call the equations the normal equations.

In this system the coefficients at unknown located on the main diagonal call square which are always positive [4]. the Coefficients at unknown symmetrized rather main diagonal are in pairs equal to a href among themselves, i.e. the system (2.13) is symmetric. Having solved this system, we find unknown dx, dy, dz. We substitute unknown in (2.11) and we find amendments.



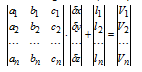
Figure 12.–Matrix type of system of the equations of poravka

or in abbreviated form:

ad+l=V (2.14)

The matrix of a has the size nxt, d–tx1, V–nx1.

We transpose a matrix of an and we multiply it at the left term by term by expression (2.14).

a^Tad+a^Tl=a^TV (2.15)

We will consider works of the matrixes entering in (2.15).



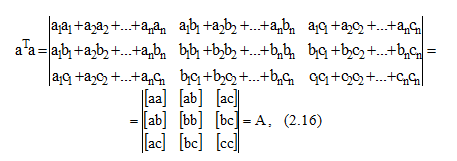
Figure 13.–Multiplication of matrixes of a^T*a

i.e. we received a matrix of coefficients of the normal equations (2.13) [10].



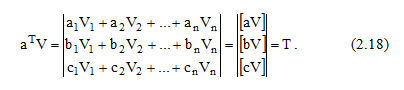
Figure 14.–Multiplication of matrixes of a^T*V

In view of (2.16) and (2.17), we come to a conclusion that the left part of expression (2.11) is no other than system of the normal equations (2.9) in a matrix form. In (2.13) and (2.15) left parts are equal [1]. Therefore, the right have to be equal to a href. Therefore we can write down

[aV]=0; [bV]=0; [cV]=0 (2.19)

The system of the normal equations assumes an air:

Ad+alfa=0 (2.20)

As the equations of amendments (2.16) are independent from each other, A matrix nonexceptional. Therefore, for the solution of the equation (2.20) it is necessary and to increase enough it at the left by A^–1 matrix, the return to A matrix. We will have as a result:

d = d=–A^–1*alfa (2.21)

We will sum up the result. adjustment is carried out in the parametrical way in such sequence:

1. We count quantity of the defined unknown t, we count number of independent measurements of n and we define number of excess measurements of r=n–t. If n=t, r=0, a problem of adjustment of the measured sizes doesn't arise.

2. Using only necessary measurements, we define one way or another approximate values of unknown x0, y0, z0., t0.

3. We work out the equations of amendments to a general view (2.7), we lead them to a linear look (2.11). As a result we receive coefficients of the equations of amendments a, b, c., q.

4. We calculate free members of the equations of amendments on a formula (2.10).

5. We make a matrix of coefficients of the equations of amendments and a matrix – a column of free members of l. Size of a matrix of a (nxt), and matrix of l (nx1). We work out the equations of amendments to a matrix form (2.16).

6. We transpose a matrix.

7. We multiply the matrix equation (2.16) at the left by a^T matrix. As a result we receive the system of the normal equations (2.15) presented in a matrix form (2.21).

8. We find A^–1 matrix, the return to a matrix of coefficients of the normal equations of A. Size of that and other matrix of txt.

9. We multiply the equation (2.21) at the left by A^–1 matrix. As a result we receive a vector column of amendments d. tx1 matrix size.

10. We calculate on a formula (2.8) the balanced values of unknown x, y..., t.

11. We substitute d vector column in the equation (2.15), we multiply and we put matrixes. As a result we receive a matrix column of amendments to the measured sizes V. nx1 matrix size. We calculate the balanced Li+Vi values.

12. We estimate the accuracy of the unknown sizes x, y received as a result of adjustment., t [7].

Conclusion

At implementation of the analysis of methods standard literature and various the Internet the sources describing the most rational application of this or that method of adjustment was analysed.

At the time of writing of the paper was the program is written to MathCAD on realization of adjustment of geodetic networks Cauchy's by method by me, adjustment of uniformally precise and not uniformally precise measurements was executed and the analysis in comparison of the results calculated on Cauchy's method and a method of the smallest squares is made.

On the basis of the obtained data we can draw a conclusion that use of a method of the smallest squares is more preferable to performance of adjustment of geodetic networks since the assessment with a bigger accuracy is calculated.

It is planned carrying out further researches.

At the time of writing of the paper, the Master's thesis isn't finished yet. The full text of work and materials on a subject can be received at the author or his head after December, 2015.

References

1. Метод наименьших квадратов. – [Электронный ресурс] –http://geodesy-book.narod.ru/Numerical_methods/05.pdf
2. Метод наименьших квадратов и основы теории обработки наблюдений/ Ю. В. Линник. –М.:Государственное издательство физико-математической литературы, 1958 – с. 338.
3. Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений: Учебное пособие для вузов.– М.:Недра, 1984, 352 с.
4. Теория матриц./Ланкастер П. – М.: Наука, 1982. – 272 с.
5. Чернова Н.И. Теория вероятностей: Учеб. пособие/ Сиб-ГУТИ. Новосибирск, 2007. – 128с.
6. Губанов В.С. Обобщенный метод наименьших квадратов. Теория и применение в астрометрии. – М.: Наука, 1997. – 319с.
7. Чеботарев А.С. Способ наименьших квадратов. – М.: Геодезический факультет и военно-геодезическое отделение Московского межевого института, Издательство Московского высшего технического училища, 1928. – 475 с.
8. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.: Физматгиз, 1963, 734 с.
9. Методы и приборы высокоточных геодезических измерений в строительстве./ Под редакцией В.Д. Большакова. – М.: Недра, 1976.– 335 с.
10. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: – Наука. Главная редакция физико-математической литературы. 1984. – 320 с.