 ,
,КОРРЕКЦИЯ ОПТИМАЛЬНЫХ ПО ТЕПЛОВЫМ ПОТЕРЯМ ДИАГРАММ ОТРАБОТКИ ПЕРЕМЕЩЕНИЙ С УЧЕТОМ ЭФФЕКТА КВАНТОВАНИЯ ПО ВРЕМЕНИ
Розкаряка П.И.
Донецкий национальный технический университет
The procedure of formation position profile correction was offered. The procedure allows for sampling time effect. The profile is optimal by heat loss and ensures nodal point switching at the instant of time, which is divisible of sample time of discrete-time commanded position. The correction ensures precision realization of position electric drive profiles.
Введение. Уменьшение тепловых потерь в позиционных электроприводах, работающих в повторно-кратковременных режимах, возможно за счет выбора оптимальной диаграммы отработки перемещения. Минимальные тепловые потери обеспечиваются при использовании параболической тахограммы. Учет момента статического сопротивления и ограничений на скорость и ускорение (и/или ток) позволяют сформировать квазиоптимальные по тепловым потерям диаграммы [1] с помощью задающих устройств (ЗУ), которые из-за своей сложности могут быть успешно реализованы только в цифровом виде. В рассматриваемых диаграммах аналоговый сигнал задания на ускорение представляет собой кусочно-линейную кривую с несколькими точками излома (назовем их узловыми точками), координаты которых рассчитываются по известным формулам [1]. Методика формирования цифровых диаграмм задания на ускорение, скорость и перемещение электромеханических систем приведены в [2]. Первым этапом этой методики является коррекция координат узловых точек оптимальных диаграмм с учетом эффекта квантования по времени. Суть коррекции заключается в обеспечении кратности периоду дискретности абсцисс точек излома и в последующем перерасчете ординат этих точек для кривой задания на ускорение таким образом, чтобы при уточненных абсциссах не изменилась величина отрабатываемого перемещения.
Целью работы является разработка методики и вывод формул для коррекции координат узловых точек кривой задания на ускорение при формировании цифровых сигналов управления, обеспечивающих минимизацию тепловых потерь в позиционных электроприводах, с учетом эффекта квантования по времени.
Материал и результаты исследования. Задатчики положения можно строить замкнутыми [3] и разомкнутыми. Недостатком замкнутых ЗУ при реализации в цифровом виде является возникновение автоколебаний в выходном сигнале, для случая разомкнутого ЗУ пренебрежение эффектом дискретизации приводит к ошибке в эталонном сигнале задания на положение [2]. Реализация алгоритмов формирования несимметричных диаграмм ускорения, оптимальных по тепловым потерям, которые имеют место при учете статического момента и ограничений на скорость и ускорение, в замкнутом виде затруднена. Поэтому рассмотрим последовательность формирования сигнала задания на положение цифрового ЗУ в разомкнутом виде. Для реализации такого ЗУ достаточно сформировать сигнал задания на ускорение, а координаты желаемой скорости и перемещения можно получить его последовательным интегрированием. На рис. 1 представлены шесть возможных разновидностей диаграмм отработки заданного перемещения с учетом статического момента и ограничений на координаты, реализующих оптимальное (или квазиоптимальное) управление по тепловым потерям.
Предлагаемая методика коррекции координат узловых точек диаграммы ускорения состоит из следующих этапов:
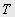 , суммарное желаемое время отработки заданного перемещения
, суммарное желаемое время отработки заданного перемещения  :
:
 , , |
(1) |
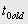 – значение времени до округления,
– значение времени до округления, 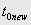 – значение времени после округления;
– значение времени после округления; …
… 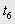 по формулам, приведенным в [1] и предназначенным для реализации ЗУ в аналоговом виде;
по формулам, приведенным в [1] и предназначенным для реализации ЗУ в аналоговом виде; ,
,  и
и  , соответствующие участкам работы с постоянным ускорением, округляем до ближайших больших, кратных периоду дискретности
, соответствующие участкам работы с постоянным ускорением, округляем до ближайших больших, кратных периоду дискретности 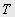 , аналогично (1), а время
, аналогично (1), а время 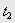 – по правилам округления (т.е. до ближайшего из целых чисел):
– по правилам округления (т.е. до ближайшего из целых чисел): ; ; |
(2) |
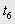 или
или 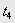 , не изменяя общего времени :
, не изменяя общего времени : , , 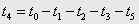 ; ; |
(3) |
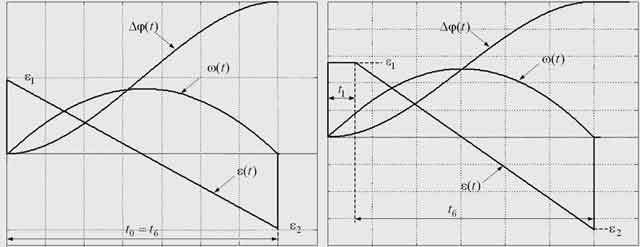

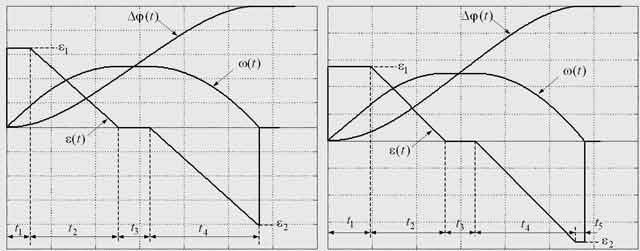
Рисунок 1 – Оптимальные и квазиоптимальные по тепловым потерям диаграммы отработки заданного перемещения
5) производим перерасчет значений ускорений при разгоне и торможении
и торможении  из условия обеспечения отработки заданного перемещения с новыми значениями времен
из условия обеспечения отработки заданного перемещения с новыми значениями времен  -
- 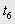 , решая систему уравнений:
, решая систему уравнений: 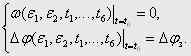 |
(4) |
Следует отметить, что приведенная методика не предусматривает повторной проверки откорректированных параметров на достижение ими уровней ограничения и изменения вида диаграммы по сравнению с исходным вариантом. При этом может только нарушиться равенство рывков на участках и . Необходимо также иметь в виду, что полученные вследствие коррекции значения , и могут оказаться несколько выше своих уровней ограничения. Если это не допустимо, то все временные интервалы следует округлять с избытком, что приведет к увеличению времени .
Выводы
ЛИТЕРАТУРА