Аннотация
Макурин А. В., Морозов Д. И. - Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции. Определены проблемы, характерные для динамики механизма передвижения крана. Выполнено построение расчетной динамической схемы и цифровой модели (пакет MATLAB среда Simulink) механизма передвижения мостового крана. Получены графики скоростей и усилий в металлоконструкциях крана.
Введение.
В современном сталеплавильном производстве роль технологических кранов трудно переоценить, их количество в конвертерном цехе может достигать нескольких десятков. Для принятия мер по их надежной работе и снижению износа механизмов передвижения необходимо провести исследование динамики механизма передвижения крана, что является целью данной работы.
Материалы исследования.
Для анализа динамических процессов в механизме передвижения можно использовать двух-, трех- и многомассовые расчетные схемы. В частности, замена трехмассовой системы на двухмассовую позволяет упростить расчет и в ряде случаев дает возможность получить удобные для анализа несложные формулы. Трехмассовая модель показывает взаимодействие между раскачивающимся грузом и двумя частями крана, имеющими упругую связь через поперечную балку. Для анализа упругих колебаний в продольных балках и в случае применения систем синхронного вращения (ССВ) более логичным является использовать многомассовые схемы с учетом масс колес, двигателей и упругостей продольных балок крана, так как часто в ССВ возникают слабозатухающие колебания, и в этом случае интересно их взаимодействие с механизмом передвижения.
В данной статье рассматриваются процессы в мосте крана при продольном перемещении. При этом мост крана представлен в виде семимассовой системы, подвес груза принят жестким. Установлено [1], что учет гибкости каната, с помощью которого подвешен груз, несущественно (не более 10 %) сказывается на значениях наибольших динамических нагрузок в упругих связях, поэтому при их определении в механизмах передвижения можно использовать систему с упругим механизмом и жестким подвесом груза. Кроме того, приняты следующие допущения: не рассматривается поперечное движение, не рассматривается динамика двигателей и электропривода.
Для рассмотрения процессов в механизмах передвижения грузоподъемных кранов изобразим элементы конструкций на схеме. Расчетная семи-массовая динамическая схема механизма передвижения представлена на рис. 1. Она содержит: две приведенные массы m1k, m2k рабочих колес (с электродвигателями), две приведенные массы холостых колес m3k, m4k, массы m1, m2 торцевых балок крана (масса поперечной балки крана равномерно распределяется между m1 и m2, масса тележки учитывается в массе m2), массу груза m3; упругие связи учтены коэффициентами жесткости: c12 – поперечной балки крана, c1, c2, c3, c4 – половин торцевых балок крана; Lп – длина подвеса груза; F12 – упругая сила в поперечной балке крана; F1, F2, F3, F4 - усилия в торцевых балках крана; V1k, V2k, V3k, V4k, V1, V2 - линейные скорости колес крана и центральных точек 1,2 торцевых балок моста крана; x - линейное перемещение груза относительно точки 2 подвеса груза; Δφ - угол перекоса поперечной балки крана.
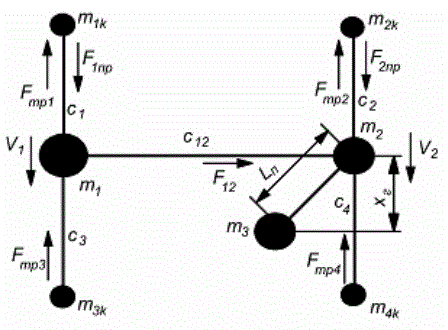
Рисунок 1 – Расчетная динамическая схема
механизма передвижения крана.
При работе механизма возникают колебания в его металлоконструкциях и трансмиссионных валах (из-за наличия упругой связи между массами m1 и m2), кроме того, происходит раскачивание груза (который вместе с канатом длиной Lп образует маятник с подвижной точкой подвеса). Динамические нагрузки в упругих связях механизмов передвижения могут в 3-7 и более раз превысить статические загрузки [1], а маятниковые колебания груза вызывают неравномерное движение механизмов передвижения кранов или тележек и создают неудобства при их эксплуатации.
Таким образом, при работе крана необходимо обеспечить:
- Ограничение динамических нагрузок в упругих связях при переходных процессах пуска или торможения, когда эти нагрузки достигают наибольших значений;
- Ограничение угла перекоса металлоконструкций крана для уменьшения износа реборд колес и рельсового пути;
- Уменьшение раскачивания подвешенного на канате груза путем разработки рациональных способов успокоения его колебаний.
Для решения вышеназванных проблем необходима соответствующая система управления краном, которая обеспечивала бы синхронность движения продольных балок крана. Но часто системы синхронного вращения имеют склонность к колебаниям, поэтому их взаимодействие с механизмом передвижения представляет большой интерес. Для изучения такого взаимодействия необходима модель механизма передвижения, построенная на базе расчетной схемы (рис. 1) в одном из пакетов прикладного моделирования, например в MATLAB / Simulink (рис. 2). В качестве параметров объекта для моделирования приняты данные ковшевого крана грузоподъемностью 100 т конвертерного цеха Алчевского металлургического комбината (m1k = m2k = m3k = m4k = 31250 кг, m1 =42500 кг, m2 = 127500 кг, m3 = 100000 кг, c12 = 2.5·106 Нм, c1 = c2 = c3 = c4 = 20·106 Нм, Lп = 5м, коэффициент трения kтр = 0.0062). На представленной модели исследовалась динамика моста при приложенных внешних усилиях 21700 Н к каждому колесу в течение 10-ти секунд с последующим выбегом под действием сил сопротивления.
На графиках показаны усилия в продольной (рис. 3,а), поперечной (рис. 3,б) балках крана и линейные скорости колес 1, 2 (рис. 4).
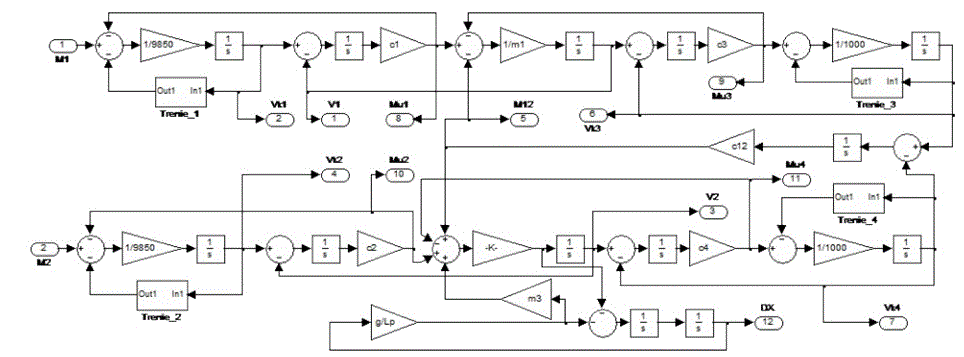
Рисунок 2 – Структура цифровой модели механизма передвижения крана.
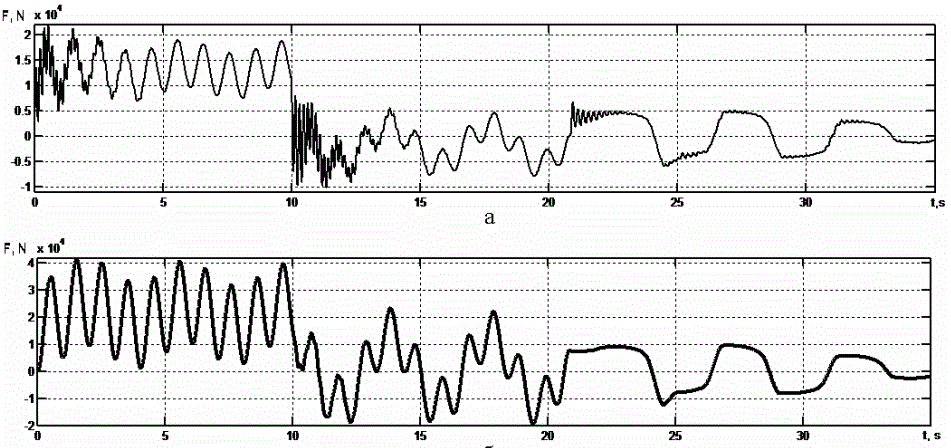
Рисунок 3 – Графики переходных процессов: а – упругой силы F1 в продольной балке;
б – упругой силы F12 в поперечной балке.

Рисунок 4 – Графики переходных процессов скоростей колес Vk1 , Vk2.
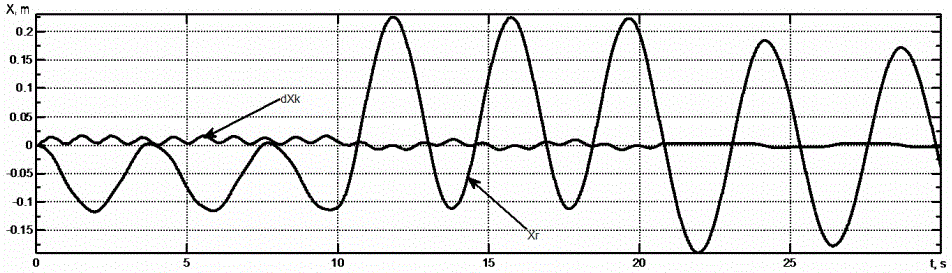
Рисунок 5 – Графики изменения относительных перемещений груза x и сторон крана Δxк.
Из графиков видно, что колебания момента и скорости имеют три составляющие: колебания подвешенного груза ω0 = 1,25 рад/с; колебания, обусловленные податливостью поперечной балки ω0 = 6 рад/с; колебания, обусловленные податливостью продольных балок, ω0 = 40 рад/с. Все три вида колебаний имеют разные частоты, что позволяет рассматривать их на более простых двухмассовых моделях. Но при использовании на механизме передвижения систем синхронного вращения, которые часто склонны к колебаниям, лучше подойдет предложенная модель, так как она учитывает взаимодействие ССВ и механизма на разных частотах колебаний. На рис.5 показано отклонение груза относительно точки подвеса и линейное рассогласование пути, пройденного сторонами крана. При данных нагрузках рассогласование пути сторон Δxк не превышает 0,025 м, относительное раскачивание груза xг не более 0,25 м
Вывооды.
При исследовании динамики мостового крана без поперечного смещения установлено: по семимассовой модели при приложении движущего усилия возникают механические колебания, в которых наблюдается три частоты взаимодействия. Для конструкций крана, рассмотренного в статье, эти частоты составляют 0,2, 0,95 и 6,4 Гц. Для исследования более полной картины процессов необходимо рассмотрение поперечного смещения крана и динамики электропривода перемещения.
Список использованной литературы
1. Масандилов Л. Б. Электропривод подъемных кранов / Масандилов Л. Б. – М.: МЭИ, 1998. – 100 с.